Регрессионный анализ как метод статистического анализа

Регрессионный анализ — статистический метод исследования зависимости случайной величины от переменных

В статистическом моделировании регрессионный анализ представляет собой исследования, применяемые с целью оценки взаимосвязи между переменными. Этот математический метод включает в себя множество других методов для моделирования и анализа нескольких переменных, когда основное внимание уделяется взаимосвязи между зависимой переменной и одной или несколькими независимыми. Говоря более конкретно, регрессионный анализ помогает понять, как меняется типичное значение зависимой переменной, если одна из независимых переменных изменяется, в то время как другие независимые переменные остаются фиксированными.

Во всех случаях целевая оценка является функцией независимых переменных и называется функцией регрессии. В регрессионном анализе также представляет интерес характеристика изменения зависимой переменной как функции регрессии, которая может быть описана с помощью распределения вероятностей.

Данный статистический метод исследования широко используется для прогнозирования, где его использование имеет существенное преимущество, но иногда это может приводить к иллюзии или ложным отношениям, поэтому рекомендуется аккуратно его использовать в указанном вопросе, поскольку, например, корреляция не означает причинно-следственной связи.

Разработано большое число методов для проведения регрессионного анализа, такие как линейная и обычная регрессии по методу наименьших квадратов, которые являются параметрическими. Их суть в том, что функция регрессии определяется в терминах конечного числа неизвестных параметров, которые оцениваются из данных. Непараметрическая регрессия позволяет ее функции лежать в определенном наборе функций, которые могут быть бесконечномерными.

Как статистический метод исследования, регрессионный анализ на практике зависит от формы процесса генерации данных и от того, как он относится к регрессионному подходу. Так как истинная форма процесса данных, генерирующих, как правило, неизвестное число, регрессионный анализ данных часто зависит в некоторой степени от предположений об этом процессе. Эти предположения иногда проверяемы, если имеется достаточное количество доступных данных. Регрессионные модели часто бывают полезны даже тогда, когда предположения умеренно нарушены, хотя они не могут работать с максимальной эффективностью.

В более узком смысле регрессия может относиться конкретно к оценке непрерывных переменных отклика, в отличие от дискретных переменных отклика, используемых в классификации. Случай непрерывной выходной переменной также называют метрической регрессией, чтобы отличить его от связанных с этим проблем.

Самая ранняя форма регрессии — это всем известный метод наименьших квадратов. Он был опубликован Лежандром в 1805 году и Гауссом в 1809. Лежандр и Гаусс применили метод к задаче определения из астрономических наблюдений орбиты тел вокруг Солнца (в основном кометы, но позже и вновь открытые малые планеты). Гаусс опубликовал дальнейшее развитие теории наименьших квадратов в 1821 году, включая вариант теоремы Гаусса-Маркова.

Термин «регресс» придумал Фрэнсис Гальтон в XIX веке, чтобы описать биологическое явление. Суть была в том, что рост потомков от роста предков, как правило, регрессирует вниз к нормальному среднему. Для Гальтона регрессия имела только этот биологический смысл, но позже его работа была продолжена Удни Йолей и Карлом Пирсоном и выведена к более общему статистическому контексту. В работе Йоля и Пирсона совместное распределение переменных отклика и пояснительных считается гауссовым. Это предположение было отвергнуто Фишером в работах 1922 и 1925 годов. Фишер предположил, что условное распределение переменной отклика является гауссовым, но совместное распределение не должны быть таковым. В связи с этим предположение Фишера ближе к формулировке Гаусса 1821 года. До 1970 года иногда уходило до 24 часов, чтобы получить результат регрессионного анализа.

Методы регрессионного анализа продолжают оставаться областью активных исследований. В последние десятилетия новые методы были разработаны для надежной регрессии; регрессии с участием коррелирующих откликов; методы регрессии, вмещающие различные типы недостающих данных; непараметрической регрессии; байесовские методов регрессии; регрессии, в которых переменные прогнозирующих измеряются с ошибкой; регрессии с большей частью предикторов, чем наблюдений, а также причинно-следственных умозаключений с регрессией.

Модели регрессионного анализа включают следующие переменные:

• Неизвестные параметры, обозначенные как бета, которые могут представлять собой скаляр или вектор.
• Независимые переменные, X.
• Зависимые переменные, Y.

В различных областях науки, где осуществляется применение регрессионного анализа, используются различные термины вместо зависимых и независимых переменных, но во всех случаях регрессионная модель относит Y к функции X и β.

Приближение обычно оформляется в виде E (Y | X) = F (X, β). Для проведения регрессионного анализа должен быть определен вид функции f. Реже она основана на знаниях о взаимосвязи между Y и X, которые не полагаются на данные. Если такое знание недоступно, то выбрана гибкая или удобная форма F.

Предположим теперь, что вектор неизвестных параметров β имеет длину k. Для выполнения регрессионного анализа пользователь должен предоставить информацию о зависимой переменной Y:

• Если наблюдаются точки N данных вида (Y, X), где N точки к данным. В этом случае имеется достаточно информации в данных, чтобы оценить уникальное значение для β, которое наилучшим образом соответствует данным, и модель регрессии, когда применение к данным можно рассматривать как переопределенную систему в β.

В последнем случае регрессионный анализ предоставляет инструменты для:

• Поиска решения для неизвестных параметров β, которые будут, например, минимизировать расстояние между измеренным и предсказанным значением Y.
• При определенных статистических предположениях, регрессионный анализ использует избыток информации для предоставления статистической информации о неизвестных параметрах β и предсказанные значения зависимой переменной Y.

Рассмотрим модель регрессии, которая имеет три неизвестных параметра: β, β₁ и β₂. Предположим, что экспериментатор выполняет 10 измерений в одном и том же значении независимой переменной вектора X. В этом случае регрессионный анализ не дает уникальный набор значений. Лучшее, что можно сделать, оценить среднее значение и стандартное отклонение зависимой переменной Y. Аналогичным образом измеряя два различных значениях X, можно получить достаточно данных для регрессии с двумя неизвестными, но не для трех и более неизвестных.

Если измерения экспериментатора проводились при трех различных значениях независимой переменной вектора X, то регрессионный анализ обеспечит уникальный набор оценок для трех неизвестных параметров в β.

В случае общей линейной регрессии приведенное выше утверждение эквивалентно требованию, что матрица X Т X обратима.

Когда число измерений N больше, чем число неизвестных параметров k и погрешности измерений ε_i, то, как правило, распространяется затем избыток информации, содержащейся в измерениях, и используется для статистических прогнозов относительно неизвестных параметров. Этот избыток информации называется степенью свободы регрессии.

Классические предположения для регрессионного анализа включают в себя:

• Выборка является представителем прогнозирования логического вывода.
• Ошибка является случайной величиной со средним значением нуля, который является условным на объясняющих переменных.
• Независимые переменные измеряются без ошибок.
• В качестве независимых переменных (предикторов) они линейно независимы, то есть не представляется возможным выразить любой предсказатель в виде линейной комбинации остальных.
• Ошибки являются некоррелированными, то есть ковариационная матрица ошибок диагоналей и каждый ненулевой элемент являются дисперсией ошибки.
• Дисперсия ошибки постоянна по наблюдениям (гомоскедастичности). Если нет, то можно использовать метод взвешенных наименьших квадратов или другие методы.

Эти достаточные условия для оценки наименьших квадратов обладают требуемыми свойствами, в частности эти предположения означают, что оценки параметров будут объективными, последовательными и эффективными, в особенности при их учете в классе линейных оценок. Важно отметить, что фактические данные редко удовлетворяют условиям. То есть метод используется, даже если предположения не верны. Вариация из предположений иногда может быть использована в качестве меры, показывающей, насколько эта модель является полезной. Многие из этих допущений могут быть смягчены в более продвинутых методах. Отчеты статистического анализа, как правило, включают в себя анализ тестов по данным выборки и методологии для полезности модели.

Кроме того, переменные в некоторых случаях ссылаются на значения, измеренные в точечных местах. Там могут быть пространственные тенденции и пространственные автокорреляции в переменных, нарушающие статистические предположения. Географическая взвешенная регрессия — единственный метод, который имеет дело с такими данными.

В линейной регрессии особенностью является то, что зависимая переменная, которой является Y_i, представляет собой линейную комбинацию параметров. Например, в простой линейной регрессии для моделирования n-точек используется одна независимая переменная, x_i, и два параметра, β и β₁.

При множественной линейной регрессии существует несколько независимых переменных или их функций.

При случайной выборке из популяции ее параметры позволяют получить образец модели линейной регрессии.

В данном аспекте популярнейшим является метод наименьших квадратов. С помощью него получают оценки параметров, которые минимизируют сумму квадратов остатков. Такого рода минимизация (что характерно именно линейной регрессии) этой функции приводит к набору нормальных уравнений и набору линейных уравнений с параметрами, которые решаются с получением оценок параметров.

При дальнейшем предположении, что ошибка популяции обычно распространяется, исследователь может использовать эти оценки стандартных ошибок для создания доверительных интервалов и проведения проверки гипотез о ее параметрах.

Пример, когда функция не является линейной относительно параметров, указывает на то, что сумма квадратов должна быть сведена к минимуму с помощью итерационной процедуры. Это вносит много осложнений, которые определяют различия между линейными и нелинейными методами наименьших квадратов. Следовательно, и результаты регрессионного анализа при использовании нелинейного метода порой непредсказуемы.

Здесь, как правило, нет согласованных методов, касающихся числа наблюдений по сравнению с числом независимых переменных в модели. Первое правило было предложено Доброй и Хардином и выглядит как N = t^n, где N является размер выборки, n — число независимых переменных, а t есть числом наблюдений, необходимых для достижения желаемой точности, если модель имела только одну независимую переменную. Например, исследователь строит модель линейной регрессии с использованием набора данных, который содержит 1000 пациентов (N). Если исследователь решает, что необходимо пять наблюдений, чтобы точно определить прямую (м), то максимальное число независимых переменных, которые модель может поддерживать, равно 4.

Несмотря на то что параметры регрессионной модели, как правило, оцениваются с использованием метода наименьших квадратов, существуют и другие методы, которые используются гораздо реже. К примеру, это следующие методы:

• Байесовские методы (например, байесовский метод линейной регрессии).
• Процентная регрессия, использующаяся для ситуаций, когда снижение процентных ошибок считается более целесообразным.
• Наименьшие абсолютные отклонения, что является более устойчивым в присутствии выбросов, приводящих к квантильной регрессии.
• Непараметрическая регрессия, требующая большого количества наблюдений и вычислений.
• Расстояние метрики обучения, которая изучается в поисках значимого расстояния метрики в заданном входном пространстве.

Все основные статистические пакеты программного обеспечения выполняются с помощью наименьших квадратов регрессионного анализа. Простая линейная регрессия и множественный регрессионный анализ могут быть использованы в некоторых приложениях электронных таблиц, а также на некоторых калькуляторах. Хотя многие статистические пакеты программного обеспечения могут выполнять различные типы непараметрической и надежной регрессии, эти методы менее стандартизированы; различные программные пакеты реализуют различные методы. Специализированное регрессионное программное обеспечение было разработано для использования в таких областях как анализ обследования и нейровизуализации.

источник

Регрессионный анализ позволяет установить аналитическую зависимость, которая показывает, как изменяется среднее значение результативного признака под влиянием одной или нескольких независимых величин. При этом множество прочих факторов, также оказывающих влияние на результативный признак, принимаются за постоянные или средние уровни. Таким образом, регрессионный анализ позволяет судить, насколько в среднем одна величина, например у, изменяется при соответствующих изменениях другой величины х, и наоборот, в какой мере переменная величина х изменяется на единицу изменения величины у.

Динамика взаимной зависимости между переменными величинами получила название регрессии, а методика исследования регрессии носит название регрессионного анализа.

Уравнение регрессии представляет собой математическую модель, в которой усредненное значение результативного признака у_х рассматривается как функция одного или нескольких факторных признаков. В первом случае речь идет об уравнении регрессии, характеризующем однофакторную (парную) зависимость между переменными, во втором — о многофакторном регрессионном анализе.

Регрессионный анализ позволяет осуществлять:

• • построение эмпирических графиков (линий) регрессии (регрессия х по у и регрессия у по х);
• • поиск уравнений, позволяющих по эмпирическим данным построить теоретическую, т.е. выровненную линию регрессии;
• • вычисление коэффициентов, позволяющих судить о двусторонней связи, т.е. насколько в среднем результирующая величина изменяется при соответствующих изменениях факторного признака.

Рассмотрим однофакторную линейную регрессию.

Эмпирические графики, отражающие взаимосвязь двух признаков, изображаются в виде диаграммы рассеяния. В декартовой системе координат по оси абсцисс откладывают значения факторного признака х (регрессора), а по оси ординат — результативного у.

Каждой паре значений (х, у) будет соответствовать конкретная точка на плоскости графика. Графическое изображение эмпирических данных, полученных в результате выборочного наблюдения, может представлять собой множество точек, которое принято называть диаграммой рассеяния.

При построении диаграммы возможны различные случаи (рис. 7.8).

Рис. 7.8. Диаграммы рассеяния а — связь отсутствует; б — связь положительная линейная; в — связь отрицательная линейная; г — связь параболическая

На рис. 7.8,а представлена диаграмма рассеяния, состоящая из множества точек, расположенных без какой-либо закономерности, что свидетельствует об отсутствии связи между переменными величинами х и у.

Чем сильнее связь между признаками, тем сильнее будут группироваться эмпирические данные, образуя линию, отражающую конкретную форму связи. Диаграмма рассеяния, изображенная на рис. 7.8,6, говорит о наличии положительной линейной зависимости между переменными величинами. С увеличением переменной величины л: значения у возрастают.

Точки, показанные на рис. 7.8,в, свидетельствуют о наличии отрицательной линейной связи. По мере увеличения значений х величины у уменьшаются.

Расположение точек на рис. 7.8,г показывает наличие нелинейной (параболической) зависимости между переменными величинами хну.

Найти уравнение регрессии и графически построить теоретическую линию регрессии по эмпирическим данным — значит определить связь средней величины результативного признака у_х с конкретными значениями факторного признака х_г

Аналитически зависимости между социально-экономическими показателями могут быть представлены простыми уравнениями в форме линейной или нелинейной связи:

— линейная зависимость;

— степенная зависимость (показательная функция);

— гиперболическая зависимость;

— парабола;

— логарифмическая функция,

где у_х — теоретические (усредненные) значения результативного признака, рассчитанные по уравнению регрессии;

а, Ь, с — коэффициенты уравнения регрессии.

Для простоты расчетов чаще всего нелинейные формы связи (путем логарифмирования или замены переменных) преобразуют в линейную форму.

При статистических исследованиях наиболее часто обращаются к анализу парной линейной формы зависимости между двумя коррелирующими признаками.

Для примера рассмотрим зависимость между ростом и весом двадцати призывников (данные условные) (табл. 7.6). Зависимость между этими переменными не может быть функциональной. Эта зависимость носит случайный характер, но при анализе достаточно большого выборочного массива можно наблюдать устойчивую статистическую взаимосвязь.

Результаты измерений веса и роста призывников

Построим эмпирическую линию регрессии по приведенным в табл. 7.6 данным (рис. 7.9).

Рис. 7.9. Зависимость между ростом и весом новобранцев

На рисунке нанесены двадцать точек, соответствующих росту и весу двадцати испытуемых. Соединив эти точки между собой, получим ломаную эмпирическую линию регрессии, которая отражает общую тенденцию возрастания веса с увеличением роста призывников.

Предположим, что зависимость между ростом и весом линейная. При этом очевидно, что рост будет являться независимой переменной, а вес — статистически зависимой переменной. Требуется найти теоретическую линию регрессии/* = а + Ьх, которую можно использовать для предсказания возможного веса у_х в зависимости от роста испытуемого.

Маловероятно, что прямые А и В (см. рис. 7.9) совпадут с теоретической линией регрессии. Наилучшие статистические свойства оценок параметров регрессии обеспечивает метод наименьших квадратов. Его предложил немецкий математик К. Гаусс в 1806 г. Сущность этого метода заключается в определении параметров уравнения при которых сумма квадратов отклонений фактических значений результативного признака от теоретических является величиной наименьшей:

Минимизируем сумму квадратов отклонений:

Далее определим, при каком значении а и Ь функция двух переменных 5 может достигнуть минимума. С этой целью найдем частные производные по да и дЬ и приравняем их к нулю (условия первого порядка).

Сократив каждое уравнение на —2 и раскрыв скобки, получим систему нормальных уравнений:

где п — число единиц наблюдений (объем статистической совокупности).

Решив систему уравнений, определим значения коэффициентов а и Ь уравнения регрессии

Коэффициент Ь — коэффициент регрессии, указывающий, насколько изменяется в среднем значение результативного признака при изменении факторного на единицу собственного измерения. Для его вычисления воспользуемся формулой

Параметры уравнения парной линейной регрессии могут быть также вычислены по формулам, дающим тот же результат:

Для решения системы нормальных уравнений (7.11) по эмпирическим данным необходимо и достаточно определить величины 1у, 1л, 1лу, 1л 2 .

Необходимый расчет для нашего примера произведен в табл. 7.7.

Расчет сумм для определения параметров парного линейного уравнения регрессии между ростом и весом призывников

Система нормальных уравнений для нашего примера имеет вид:

Отсюда коэффициенты: а — — 23,98; Ь = 0,55.

Определив коэффициенты а п Ь п подставив их в уравнение

регрессии у_х = а + Ьх, найдем значение у_х, зависящее только от заданного значения х.

Следовательно, искомое уравнение регрессии у по х примет вид:

Подставляя последовательно в данное уравнение значения х из табл. 7.7 (164, 165, 167 и т.д.), определим теоретические значения результативного признака у_х. Вычисленный ряд чисел поместим в последнюю графу табл. 7.7. Нанесем соответствующие точки на график, а затем, соединив их между собой, получим прямую С, которая представляет искомую теоретическую линию регрессии (см. рис. 7.9). Любая другая произвольно начерченная линия (например, А или В) не будет соответствовать условиям метода наименьших квадратов.

Положительный или отрицательный знак при коэффициенте регрессии b говорит о положительном или отрицательном направлении линии регрессии. Таким образом, регрессия х по у и у по х представляет собой ряд средних значений одной величины, соответствующей определенным значениям другой.

В Excel уравнение регрессии и величина достоверности аппроксимации R 2 (коэффициент детерминации) могут быть получены при построении диаграммы (см. приложение 8). Для этого на диаграмме необходимо правой кнопкой мыши щелкнуть по одному из маркеров и в появившемся контекстном меню выбрать опцию Добавить линию тренда. В открывшемся диалоговом окне на вкладке Тип необходимо указать тип функции, а на вкладке Параметры установить флажки возле опций Показывать уравнение на диаграмме и Поместить на диаграмму величину достоверности аппроксимации (Л Л 2).

Построение линии регрессии по данным табл. 7.6, исходные данные и результаты вычислений представлены на рис. 7.10.

Рис. 7.10 Построение линии регрессии в Excel

На практике, как правило, результаты статистического исследования содержат большой числовой массив. Чтобы упорядочить результаты выборочных наблюдений, на основе которых мы хотим определить наличие и форму связи между исследуемыми переменными, целесообразно исходный массив эмпирических данных представить в виде корреляционной таблицы. Схема построения такой таблицы приведена на рис. 7.11.

Рис. 7.11. Схема построения корреляционной таблицы при положительной зависимости между переменными х и у

В таблице расположены два сгруппированных вариационных ряда по факторному х и по результативному у признакам, имеющих общие частоты / . Число строк и столбцов, из которых состоит корреляционная таблица, соответствует числу групп (интервалов) одного и другого вариационных рядов. Каждая варианта двух сопряженных рядов занимает свою клетку в корреляционной таблице. По распределению частот можно предварительно судить о форме и частично о тесноте связи между признаками х и у. Например, распределение вариант по диагонали из левого верхнего угла таблицы к ее нижнему правому углу (см. рис. 7.11) свидетельствует о наличии положительной связи между переменными х и у. Расположение вариант в корреляционной таблице из нижнего левого угла по направлению к правому верхнему говорит о наличии отрицательной связи между исследуемыми переменными величинами х и у. Если в корреляционной таблице варианты двух сопряженных рядов распределены более или менее равномерно по всему полю таблицы, то можно говорить об отсутствии какой-либо зависимости между переменными хну.

Методику построения корреляционной таблицы покажем на условном примере. Имеются сведения о стаже работы и производительности труда у 24 рабочих (табл. 7.8).

Зависимость производительности труда от стажа работы рабочих токарного цеха

источник

Регрессионный анализ нельзя использовать для определения наличия связи между переменными, поскольку наличие такой связи и есть предпосылка для применения анализа.

Строго регрессионную зависимость можно определить следующим образом. Пусть , — случайные величины с заданным совместным распределением вероятностей. Если для каждого набора значений определено условное математическое ожидание

(уравнение регрессии в общем виде),

то функция называется регрессией величины Y по величинам , а её график — линией регрессии по , или уравнением регрессии.

Зависимость от проявляется в изменении средних значений Y при изменении . Хотя при каждом фиксированном наборе значений величина остаётся случайной величиной с определённым рассеянием.

Для выяснения вопроса, насколько точно регрессионный анализ оценивает изменение Y при изменении , используется средняя величина дисперсии Y при разных наборах значений (фактически речь идет о мере рассеяния зависимой переменной вокруг линии регрессии).

На практике линия регрессии чаще всего ищется в виде линейной функции (линейная регрессия), наилучшим образом приближающей искомую кривую. Делается это с помощью метода наименьших квадратов, когда минимизируется сумма квадратов отклонений реально наблюдаемых от их оценок (имеются в виду оценки с помощью прямой линии, претендующей на то, чтобы представлять искомую регрессионную зависимость):

(M — объём выборки). Этот подход основан на том известном факте, что фигурирующая в приведённом выражении сумма принимает минимальное значение именно для того случая, когда .

Для решения задачи регрессионного анализа методом наименьших квадратов вводится понятие функции невязки:

Условие минимума функции невязки:

Полученная система является системой линейных уравнений с неизвестными

Если представить свободные члены левой части уравнений матрицей

а коэффициенты при неизвестных в правой части матрицей

то получаем матричное уравнение: , которое легко решается методом Гаусса. Полученная матрица будет матрицей, содержащей коэффициенты уравнения линии регрессии:

Для получения наилучших оценок необходимо выполнение предпосылок МНК (условий Гаусса−Маркова). В англоязычной литературе такие оценки называются BLUE (Best Linear Unbiased Estimators) − наилучшие линейные несмещенные оценки.

Параметры являются частными коэффициентами корреляции; интерпретируется как доля дисперсии Y, объяснённая , при закреплении влияния остальных предикторов, то есть измеряет индивидуальный вклад в объяснение Y. В случае коррелирующих предикторов возникает проблема неопределённости в оценках, которые становятся зависимыми от порядка включения предикторов в модель. В таких случаях необходимо применение методов анализа корреляционного и пошагового регрессионного анализа.

Говоря о нелинейных моделях регрессионного анализа, важно обращать внимание на то, идет ли речь о нелинейности по независимым переменным (с формальной точки зрения легко сводящейся к линейной регрессии), или о нелинейности по оцениваемым параметрам (вызывающей серьёзные вычислительные трудности). При нелинейности первого вида с содержательной точки зрения важно выделять появление в модели членов вида , , свидетельствующее о наличии взаимодействий между признаками , и т. д (см. Мультиколлинеарность).

источник

Регрессионный анализ — это метод установления аналитического выражения стохастической зависимости между исследуемыми признаками. Уравнение регрессии показывает, как в среднем изменяется у при изменении любого из x_i, и имеет вид:

где у — зависимая переменная (она всегда одна);

х_i— независимые переменные (факторы) (их может быть несколько).

Если независимая переменная одна — это простой регрессионный анализ. Если же их несколько (п 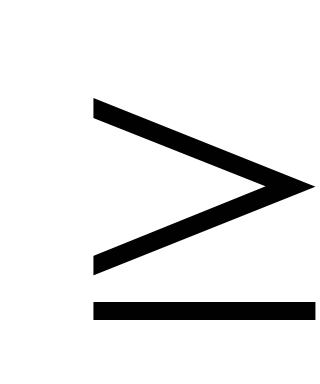2), то такой анализ называется многофакторным.

В ходе регрессионного анализа решаются две основные задачи:

построение уравнения регрессии, т.е. нахождение вида зависимости между результатным показателем и независимыми факторами x₁, x₂, …, x_n.

оценка значимости полученного уравнения, т.е. определение того, насколько выбранные факторные признаки объясняют вариацию признака у.

Применяется регрессионный анализ главным образом для планирования, а также для разработки нормативной базы.

В отличие от корреляционного анализа, который только отвечает на вопрос, существует ли связь между анализируемыми признаками, регрессионный анализ дает и ее формализованное выражение. Кроме того, если корреляционный анализ изучает любую взаимосвязь факторов, то регрессионный — одностороннюю зависимость, т.е. связь, показывающую, каким образом изменение факторных признаков влияет на признак результативный.

Регрессионный анализ — один из наиболее разработанных методов математической статистики. Строго говоря, для реализации регрессионного анализа необходимо выполнение ряда специальных требований (в частности, x_l,x₂. x_n; y должны быть независимыми, нормально распределенными случайными величинами с постоянными дисперсиями). В реальной жизни строгое соответствие требованиям регрессионного и корреляционного анализа встречается очень редко, однако оба эти метода весьма распространены в экономических исследованиях. Зависимости в экономике могут быть не только прямыми, но и обратными и нелинейными. Регрессионная модель может быть построена при наличии любой зависимости, однако в многофакторном анализе используют только линейные модели вида:

Построение уравнения регрессии осуществляется, как правило, методом наименьших квадратов, суть которого состоит в минимизации суммы квадратов отклонений фактических значений результатного признака от его расчетных значений, т.е.:

j = a + b₁x₁j + b₂x₂j + . + b_nх_nj — расчетное значение результатного фактора.

Коэффициенты регрессии рекомендуется определять с помощью аналитических пакетов для персонального компьютера или специального финансового калькулятора. В наиболее простом случае коэффициенты регрессии однофакторного линейного уравнения регрессии вида y = а + bх можно найти по формулам:

Кластерный анализ — один из методов многомерного анализа, предназначенный для группировки (кластеризации) совокупности, элементы которой характеризуются многими признаками. Значения каждого из признаков служат координатами каждой единицы изучаемой совокупности в многомерном пространстве признаков. Каждое наблюдение, характеризующееся значениями нескольких показателей, можно представить как точку в пространстве этих показателей, значения которых рассматриваются как координаты в многомерном пространстве. Расстояние между точками р и q с k координатами определяется как:

Основным критерием кластеризации является то, что различия между кластерами должны быть более существенны, чем между наблюдениями, отнесенными к одному кластеру, т.е. в многомерном пространстве должно соблюдаться неравенство:

где r_1,2 — расстояние между кластерами 1 и 2.

Так же как и процедуры регрессионного анализа, процедура кластеризации достаточно трудоемка, ее целесообразно выполнять на компьютере.

источник

Цель: Сформировать знания о сущности, роли, значении и области применения статистического и корреляционно-регрессионного анализа.

ТЕЗИСЫ ЛЕКЦИЙ

Тема 1 Статистический и регрессионный анализ

Цель: Сформировать знания о сущности, роли, значении и области применения статистического и корреляционно-регрессионного анализа.

1. Прогнозирование в экономике и его информационное обеспечение.

2.Предварительный анализ данных. Теория статистического оценивания. Теория статистической проверки гипотез.

3. Доверительные области. Доверительные интервалы для зависимой переменной.

5. Корреляционно-регрессионный анализ.

6.Использование модели множественной линейной регрессии для прогнозирования экономических показателей.

1. Прогнозирование в экономике и его информационное обеспечение.

Прогнозирование в экономике это вид управленческой деятельности. Целью прогнозирования является описание будущего состояния экономической системы в целом или отдельных ее частей в соответствии со стоящими задачами. В строгом понимании прогноз – это научный анализ возможного будущего, построение, исследование и оценка вариантов развития экономической системы. Он предполагает внесение строгого порядка в имеющуюся информацию об экономической системе в соответствии с достаточно ясно сформулированными целями прогнозирования.

Для уяснения сущности прогнозирования необходимо сравнение с планированием. Если планирование конкретно, т.е. выполняет нормативные (предписывающие) функции, то прогнозирование – дескриптивно (описательно).

Прогноз также как и планирование может быть краткосрочным (до 3 лет), среднесрочным (5-7 лет) и долгосрочным (свыше 10 лет). Следовательно, прогноз может составляться и сопутствовать соответствующему плану. В таком случае он может оценивать вероятность выполнения плана.

Результаты такого прогнозирования служит основой для разработки перспективных планов на следующий будущий период времени.

Особенностью прогнозов на длительную перспективу является формирование возможных вариантов развития экономических систем, снабженных содержательным описанием и набором количественных показателей. Систему содержательных предпосылок, на основе которых формируются варианты прогнозов, называются сценариями.

Для разработки прогноза необходима информация. Информация может быть детерминированной и вероятностной. Причемб она может быть получена в результате планирования и прогнозирования.

Естественно, что качество информации является одним из важных факторов в разработке прогноза. Качество информации непосредственно связано с достоверностью, оперативностью получения информации и научной обоснованностью. В современных условиях это достигается за счет использования информационных и компьютерных технологий и математико-статистических методов и моделей. В свою очередь последнее возможно при наличии современной компьютерной и организационной техники, наличии вычислительных сетей и возможностей использования Интернета, технических и программных средств накопления, обработки, хранения, использования и передачи информации, телекоммуникационных связей. Большое значение имеют базы и банки данных. Понятно, что качество прогноза тем выше, чем более качественнее и больше массивы необходимой информации, чем больше возможности по оперативному поиску, получению, передаче, обработке, анализу и использованию научно-обоснованной информации.

Особое место среди факторов, повышающих качество прогнозов, занимают математико-статистические методы и модели.

2. Теория статистического оценивания. Теория статистической проверки гипотез.

Теория статистического оценивания неизвестных значений параметров или функций разрабатывает математические методы и приемы, с помощью которых на основании исходных статистических данных можно вычислить как можно более точные приближенные значения (статистические оценки) для одного или нескольких числовых параметров или функций, характеризующих функционирование исследуемой системы.

Статистическая оценка строится в виде функции от результатов наблюдений и сама является величиной случайной.

В качестве основной меры точности статистической оценки неизвестного параметра Х чаще всего используется средний квадрат ее отклонения от оцениваемого значения , а в многомерном случае – ковариационная матрица компонент векторной оценки (ковариационная матрица – это матрица, образованная из попарных ковариаций случайных величин). Для К-мерного случайного вектора Х=(x₁, x₂, …, x_k) ковариационная матрица – это квадратная матрица с компонентами: d_ij = E[(x_i – Ex_i) (x_j-Ex_j)]. На главной диагонали ковариационной матрицы находится дисперсии величин x_i:d_i=Dх_i. Ковариационная матрица является симметричной, т.е. d_ij = d_ji и неотрицательно определенной). Чем меньше , тем точнее (эффективнее) оценка. Для широкого класса генеральных совокупностей существует неравенство Рао-Крамера-Фреше, задающее тот минимум (по всем возможным оценкам) среднего квадрата , улучшить который невозможно. используется в качестве начальной точки отсчета меры эффективности оценки, определив эффективность любой оценки параметра в виде отношения:

(1.2.1)

Свойство состоятельности оценки обеспечивает ее статистическую устойчивость, т.е. сходимость (по вероятности) к истинному значению оцениваемого параметра по мере роста объема выборки, на основании которой эта оценка строится.

С учетом случайной природы каждого конкретного оценочного значения неизвестного параметра представляет интерес построение целых интервалов оценочных значений , а в многомерном случае – целых областей, которые с наперед заданной (и близкой к единице) вероятностью р накрывали бы истинное значение оцениваемого параметра , т.е. . Эти интервалы (области) принято называть доверительными или интервальными оценками.

Существует два подхода к построению интервальных оценок: точный (конструктивно реализуемый лишь в сравнительно узком классе ситуаций) и асимптотически-приближенный (наиболее распространенный в практике статистических приложений).

Основными методами статистических оценок являются: метод максимального правдоподобия; метод моментов; метод наименьших квадратов; метод, использующий взвешивание наблюдений – цензурирование, урезание, порядковые статистики. Различные варианты метода, использующего и взвешивание наблюдений находят все большее распространение в связи с устойчивостью получаемых при этом статистических выводов по отношению к возможным отклонениям реального распределения исследуемой генеральной совокупности от постулируемого модельного.

Теория статистической проверки гипотез исследует процедуры сопоставления высказанной гипотезы относительно природы или величины неизвестных статистических параметров анализируемого явления с имеющимися выборочными данными.

Результат сравнения может быть отрицательным, т.е. данные наблюдения противоречат высказанной гипотезе и тогда от нее нужно отказаться либо неотрицательным, т.е. данные наблюдения не противоречат высказанной гипотезе и тогда ее можно принять в качестве допустимого решения.

По своему прикладному содержанию, высказываемые в ходе статистической обработки данных гипотезы можно подразделить на несколько основных типов:

1. Гипотезы о типе закона распределения исследуемой случайной величины. Проверка гипотез этого типа осуществляется с помощью так называемого согласия критериев и опирается на ту или иную меру различия между анализируемой эмпирической функцией распределения F(x) и гипотетическим модельным законом F_mod(x).

2. Гипотезы об однородности двух или нескольких обрабатываемых выборок или некоторых характеристик анализируемых совокупностей. Например, если имеется несколько «порций» выборочных данных:

то говорят, что соответствующие выборочные характеристики: F_i(x) – вероятностный закон, которому подчиняются наблюдения выборки; а_i – средние значения; — дисперсия и т.д. различаются статистически незначительно, т.е.:

(1.2.2)

(1.2.3)

(1.2.4)

3. Гипотезы о числовых значениях параметров исследуемой генеральной совокупности.

Например, если а – номинальное значение исследуемого параметра. Каждое отдельное значение об этом параметре х_i может отклоняться от него. Чтобы проверить исследуемое явление, например, точность настройки станка на обработку определенной детали, необходимо убедиться, что среднее значение исследуемого параметра у производимых на станке деталей будет соответствовать номиналу, т.е. проверить гипотезу:

Н : Е_у = а_i, где у – исследуемая случайная величина.

4. Гипотезы о типе зависимости между компонентами исследуемого многомерного признака.

Подобно тому как при исследовании закона распределения обрабатываемых наблюдений бывает важно правильно подобрать соответствующий модельный закон, так при исследовании статистической зависимости, например, х₂ от х₁ анализируемого двумерного признака х=(х₁, х₂) бывает важно проверить гипотезу об общем виде этой зависимости. Например, гипотезу о том, что х₂ и х₁ связаны линейной регрессионной связью, т.е.:

где: а и а₁ — некоторые неизвестные параметры модели.

Статистические критерии, с помощью которых проверяются гипотезы этого типа, часто называют критериями адекватности. По своему назначению и характеру решаемых задач они чрезвычайно разнообразны, но строятся они по одной логической схеме.

Если проверяемое предположительное утверждение сводится к гипотезе о том, что значение некоторого параметра х в точности равно заданной величине х, то эта гипотеза называется простой, в других случаях гипотеза называется сложной.

3.Доверительные области. Доверительные интервалы для зависимой переменной.

Доверительная область – это область в пространстве параметров, в которую с заданной вероятностью входит неизвестное значение оцениваемого параметра распределения. «Заданная вероятность» называется доверительной вероятностью и обычно обозначается γ. Пусть Θ – пространство параметров. Рассмотрим статистику Θ₁ = Θ₁(x₁, x₂,…, x_n) – функцию от результатов наблюдений x₁, x₂,…, x_n, значениями которой являются подмножества пространства параметров Θ. Так как результаты наблюдений – случайные величины, то Θ₁ – также случайная величина, значения которой – подмножества множества Θ, т.е. Θ₁ – случайное множество. Напомним, что множество – один из видов объектов нечисловой природы, случайные множества изучают в теории вероятностей и статистике объектов нечисловой природы.

В ряде литературных источников, к настоящему времени во многом устаревших, под случайными величинами понимают только те из них, которые в качестве значений принимают действительные числа. Согласно справочнику академика РАН Ю.В.Прохорова и проф. Ю.А.Розанова случайные величины могут принимать значения из любого множества. Так, случайные вектора, случайные функции, случайные множества, случайные ранжировки (упорядочения) – это отдельные виды случайных величин. Используется и иная терминология: термин «случайная величина» сохраняется только за числовыми функциями, определенными на пространстве элементарных событий, а в случае иных областей значений используется термин «случайный элемент». (Замечание для математиков: все рассматриваемые функции, определенные на пространстве элементарных событий, предполагаются измеримыми.)

Статистика Θ₁ называется доверительной областью, соответствующей доверительной вероятности γ, если

(1.3.1.)

Ясно, что этому условию удовлетворяет, как правило, не одна, а много доверительных областей. Из них выбирают для практического применения какую-либо одну, исходя из дополнительных соображений, например, из соображений симметрии или минимизируя объем доверительной области, т.е. меру множества Θ₁.

При оценке одного числового параметра в качестве доверительных областей обычно применяют доверительные интервалы (в том числе лучи), а не иные типа подмножеств прямой. Более того, для многих двухпараметрических и трехпараметрических распределений (нормальных, логарифмически нормальных, Вейбулла-Гнеденко, гамма-распределений и др.) обычно используют точечные оценки и построенные на их основе доверительные границы для каждого из двух или трех параметров отдельно. Это делают для удобства пользования результатами расчетов: доверительные интервалы легче применять, чем фигуры на плоскости или тела в трехмерном пространстве.

Как следует из сказанного выше, доверительный интервал – это интервал, который с заданной вероятностью накроет неизвестное значение оцениваемого параметра распределения. Границы доверительного интервала называют доверительными границами. Доверительная вероятность γ – вероятность того, что доверительный интервал накроет действительное значение параметра, оцениваемого по выборочным данным. Оцениванием с помощью доверительного интервала называют способ оценки, при котором с заданной доверительной вероятностью устанавливают границы доверительного интервала.

Для числового параметра θ рассматривают верхнюю доверительную границу θ_В, нижнюю доверительную границу θ_Н и двусторонние доверительные границы – верхнюю θ_1В и нижнюю θ_1Н. Все четыре доверительные границы – функции от результатов наблюдений x₁, x₂,…, x_n и доверительной вероятности γ.

Верхняя доверительная граница θ_В – случайная величина θ_В = θ_В(x₁, x₂,…, x_n; γ), для которой Р(θ θ_H) = γ, где θ – истинное значение оцениваемого параметра. Доверительный интервал в этом случае имеет вид [θ_H; +∞).

(1.3.4),

т.е. в качестве нижней доверительной границы θ_Н, соответствующей доверительной вероятности γ, следует взять

. (1.3.5)

(1.3.6).

Поскольку распределение Стьюдента симметрично относительно 0, то = — . Следовательно, в качестве верхней доверительной границы θ_В для m, соответствующей доверительной вероятности γ, следует взять

. (1.3.7)

Как построить двусторонние доверительные границы? Положим

где θ_1Н и θ_1В заданы формулами (1.3.5) и (1.3.7) соответственно. Поскольку неравенство θ_1Н0,5; γ₂ > 0,5). Следовательно, если γ = γ₁ + γ₂ – 1, то θ_1Н и θ_1В – двусторонние доверительные границы для m, соответствующие доверительной вероятности γ. Обычно полагают γ₁ = γ₂, т.е. в качестве двусторонних доверительных границ θ_1Н и θ_1В, соответствующих доверительной вероятности γ, используют односторонние доверительные границы θ_Н и θ_В, соответствующие доверительной вероятности (1+γ)/2.

Другой вид правил построения доверительных границ для параметра θ основан на асимптотической нормальности некоторой точечной оценки θ_n этого параметра. В вероятностно-статистических методах принятия решений используют, как уже отмечалось, несмещенные или асимптотически несмещенные оценки θ_n, для которых смещение либо равно 0, либо при больших объемах выборки пренебрежимо мало по сравнению со средним квадратическим отклонением оценки θ_n. Для таких оценок при всех х

(1.3.10),

где Ф(х) – функция нормального распределения N(0;1). Пусть u_γ – квантиль порядка γ распределения N(0;1). Тогда

(1.3.11)

(1.3.12)

(1.3.13),

то в качестве θ_Н можно было бы взять левую часть последнего неравенства. Однако точное значение дисперсии D(θ_n) обычно неизвестно. Зато часто удается доказать, что дисперсия оценки имеет вид

(1.3.14)

(с точностью до пренебрежимо малых при росте n слагаемых), где h(θ) – некоторая функция от неизвестного параметра θ. Справедлива теорема о наследовании сходимости, согласно которой при подстановке в h(θ) оценки θ_n вместо θ соотношение (1.3.11) остается справедливым, т.е.

(1.3.15).

Следовательно, в качестве приближенной нижней доверительной границы следует взять

(1.3.16),

а в качестве приближенной верхней доверительной границы —

(1.3.17).

С ростом объема выборки качество приближенных доверительных границ улучшается, т.к. вероятности событий > θ_H> и 0, целое) случайной величины Х определяется как математическое ожидание ЕХ k случайной величины Х k , если оно существует.

Если F(Х) – функция распределения случайной величины Х, то

ЕХ k = (1.4.1)

при условии, что интеграл сходится абсолютно. В частности, если Х принимает значения х₁, х₂, х₃,…х_n с вероятностями р₁, р₂, …р_n , то

ЕХ k = . (1.4.2)

Если Х имеет плотность распределения f (х) на прямой, то

ЕХ k = , f(x) dx (1.4.3)

Примечание: плотность распределения вероятностей случайной величи6ны Х функция f(x), такая, что f(x)≥0 и , а при любых a k называется моментом порядка k относительно a, Е(х-Ех) k — центральным моментом порядка k. Центральный момент второго порядка Е(х-Ех) 2 называется дисперсией DX.

Средняя арифметическая и дисперсия вариационного ряда являются частными случаями более общего понятия о моментах вариационного ряда. Различают: начальный момент порядка q ( ) и центральный момент ( ).

С помощью центральных моментов 3 и 4 рассчитывают коэффициенты асимметрии и эксцесс.

Коэффициент асимметрии показывает скошенность (асимметрию) данных: .

Свойства коэффициента асимметрии: >0 ряд несимметричный с правосторонней асимметрией; 0 распределение островершинное; k называется абсолютным моментом порядка k. Аналогично определяется момент совместного распределения случайных величин х₁, х₂, х₃,…х_n(так называемого многомерного распределения): для любых целых k_i>0, k₁ + k₂+…k_n=K, математическое ожидание Е( ) называется смешанным моментом порядка k, а Е(х₁ – Ех₁) k1 …(х_n-EX_n) k n — центральным смешанным моментом порядка k. Смешанный момент Е(х₁-Ех₁)(х₂-Ех₂) называется ковариацией и служит одной из основанных характеристик зависимости между случайными величинами.

Если известны моменты распределения, то можно сделать некоторые утверждения о вероятностях отклонения случайной величины от ее математического ожидания в терминах неравенств. Наиболее известно неравенство Чебышева:

(1.4.5)

Задача, состоящая в определении распределения вероятностей последовательностью его моментов, носит название проблема моментов. В математической статистике для статистической оценки параметров распределения служат выборочные моменты.

Метод моментов является одним из распространенных общих методов получения статистической оценки. Заключается в приравнивании осредненного числа выборочных моментов соответствующим моментам исходного распределения, которые являются функциями от неизвестных параметров и решения полученных уравнений относительно этих параметров.

5. Корреляционно-регрессионный анализ

Корреляционный анализ – это совокупность основанных на математической теории корреляции методов обнаружения корреляционной зависимости между случайными величинами или признаками (корреляция – величина, характеризующая взаимную зависимость двух случайных величин). При этом речь не идет о выявлении формы исследуемых зависимостей (это составляет предмет исследования регрессионного анализа), а лишь об установлении самого факта статистической связи и об измерении степени ее тесноты.

В качестве основных измерителей тесноты связи между количественными переменными используются: коэффициент корреляции (индекс корреляции), корреляционное отношение, парные, частные и множественные коэффициенты корреляции, коэффициенты детерминации.

Парные и частные коэффициенты корреляции являются измерителями степени тесноты линейной связи между переменными. В этом случае корреляционные характеристики могут оказаться как положительными, так и отрицательными в зависимости от одинаковой или противоположной тенденции взаимосвязанного изменения анализируемых переменных. При положительном значении коэффициента корреляции говорят о наличии положительной линейной статистической связи, при отрицательном – об отрицательной.

Коэффициент корреляции устанавливает степень зависимости между результирующим и факторным признаками (случайными величинами) и рассчитывается по формуле:

(1.5.1),

где: х, у – случайные величины;

D_х, D_у – среднеквадратические (стандартные) отклонения;

r_xy – корреляционная функция или ковариация .

При нелинейной зависимости аналогичный показатель называется индексом корреляции.

Измерителем степени тесноты связи любой формы является корреляционное отношение, для вычисления которого необходимо разбить область значений предсказывающей переменной на интервалы группирования. Парный коэффициент корреляции позволяет измерять степень тесноты статистической связи между парой переменных без учета опосредованного или совместного влияния других показателей.

Частный коэффициент корреляции оценивает степень тесноты линейной связи между двумя переменными, очищенной от опосредованного влияния других факторов. Для его расчета необходима исходная информация как по анализируемой паре переменных, так и по всем тем переменным опосредованное, влияние которых необходимо элиминировать.

Множественный коэффициент корреляции измеряет степень тесноты статистической связи между некоторым показателем, с одной стороны, и совокупностью других переменных – с другой. Квадрат его величины (называемый коэффициентом детерминации) показывает какая доля дисперсии исследуемого результирующего показателя определяется совокупным влиянием контролируемых, объясняющих переменных. Оставшаяся необъясненной доля дисперсии результирующего показателя определяет ту верхнюю границу точности, которой можно добиться при восстановлении (прогнозировании, аппроксимации) значения результирующего показателя по заданным значениям объясняющих переменных.

В качестве основных характеристик парной статистической связи между упорядочениями используются ранговые коэффициенты корреляции Спирмэна и Кендалла. Их значения меняются в диапазоне от –1 до +1, причем экстремальные значения характеризуют связи соответственно пары прямо противоположных и пары совпадающих упорядочений, а нулевое значение рангового коэффициента корреляции получается при полном отсутствии статистической связи между анализируемыми порядковыми переменными.

В качестве основной характеристики статистической связи между несколькими порядковыми переменными используется так называемый коэффициент (согласованности) Кендалла. Между значениями этого коэффициента и значениями парных ранговых коэффициентов Спирмэна, построенных для каждой пары анализируемых переменных существуют соотношения.

Регрессионный анализ – объединяет практические методы исследования регрессионной зависимости между величинами, полученными в результате статистических наблюдений. В основе лежит понятие регрессии – зависимости среднего значения случайной величины от некоторой другой величины или нескольких величин (в последнем случае имеем множественную регрессию). Регрессионная зависимость между случайными величинами х и у характеризуется тем, что одному и тому же значению х могут соответствовать несколько значений у (например, если х – одна и та же доза минерального удобрения вносимого на 1 га почвы на разных полях, то у – урожайность разная на каждом из полей).

Уравнение, связывающее эти параметры, называется уравнением регрессии:

у = а + а₁х + (1.5.2),

где: а, а₁ — коэффициенты регрессии, которые оцениваются из статистических данных.

Аналогично записывается уравнение множественной (многофакторной) регрессии:

у = а + а₁х₁, + … + а_nх_n+ (1.5.3)

Проведение регрессионного анализа условно разбивается на четыре этапа: параметризация модели; анализ мультиколинеарности и отбор наиболее информативных факторов; вычисление оценок неизвестных параметров, входящих в используемое уравнение связи; анализ эффективности полученных уравнений связи.

Таким образом, основу регрессионного анализа составляет вывод регрессионного уравнения, включающего оценку его параметров, с использованием которого находится средняя величина случайной переменной, если величина другой (других) известна. Регрессионный анализ можно считать частью теории корреляции как общей теории исследующей взаимосвязи между случайными величинами.

6.Использование модели множественной линейной регрессии для прогнозирования экономических показателей.

Множественная регрессия широко используется в решении проблем спроса, доходности акций, при изучении функции издержек производства, в макроэкономических расчетах и целого ряда других вопросов экономики.

Основная цель множественной регрессии – построить модель с большим числом факторов (два и более), определив при этом влияние каждого из них в отдельности, а также совокупное их воздействие _на моделируемый показатель.

Общий вид модели МР: у = а + а₁х₁, + … + а_nх_n+(где: х₁,х₂,…х_n — факторные признаки; а₁,а₂,… а_n — коэффициенты регрессии при переменных х₁,х₂,…х_n, — случайная ошибка). Проблема спецификации включает в себя два круга вопросов: отбор факторов и выбор вида уравнения регрессии.

Факторы, включаемые во множественную регрессию, должны отвечать следующим требованиям: они должны быть количественно измеримы; факторы не должны быть интеркоррелированы (интеркорреляция – корреляция между объясняющими переменными) и тем более находиться в точной функциональной зависимости.

Если между факторами существует высокая корреляция, то нельзя определить их изолированное влияние на результативный признак и параметры уравнения регрессии оказываются не интерпретируемыми. Если строится модель с набором p факторов, то для нее рассчитывается показатель детерминации , который фиксирует долю объясненной вариации результативного признака за счет рассматриваемых в регрессии факторов. Влияние других не учтенных в модели факторов оценивается как 1- с соответствующей остаточной дисперсией ( ).

При дополнительном включении в регрессию p+1 фактора должен возрастать, а уменьшаться: и . Если этого не происходит, то включаемый в анализ фактор не улучшает модель и является лишним фактором.

Отбор факторов осуществляется в две стадии: на первой подбираются факторы исходя из сущности проблемы; на второй – на основе матрицы показателей корреляции.

Как и в парной регрессии различают линейные и нелинейные уравнения множественной регрессии (МР).

В линейной МР параметры при х ( ) называются коэффициентами «чистой» регрессии, которые характеризуют среднее изменение результата с изменением соответствующего фактора на единицу при неизменном значении других факторов, закрепленных на среднем уровне. Параметр а не подлежит экономической интерпретации.

Стандартные компьютерные программы обработки регрессионного анализа позволяют перебирать различные функции и выбирать ту, для которой и ошибка аппроксимации минимальны, а коэффициент детерминации ( ) максимален.

Практическая значимость уравнения множественной регрессии оценивается с помощью показателя множественной корреляции и его квадрата – коэффициента детерминации.

Показатель множественной корреляции оценивает тесноту совместного влияния факторов на результат.

Значимость уравнения множественной регрессии в целом оценивается с помощью F-критерия Фишера: (где: — факторная сумма квадратов отклонений на одну степень свободы; — остаточная сумма квадратов на одну степень свободы; — коэффициент (индекс) множественной детерминации; — число параметров при переменных х; — число наблюдений.

Считается, что две переменные явно коллинеарны, т.е. находятся между собой в линейной зависимости, если (r_x1x2 – коэффициент корреляции, отражающий межфакторную связь между признаками х₁ и х₂). Если факторы явно коллинеарны, то они дублируют друг друга и один из них рекомендуется исключить из регрессии. Предпочтение при этом отдается тому фактору, который при достаточно тесной связи с результатом имеет наименьшую тесноту связи с другими факторами.

Включение в модель мультиколлинеарных факторов нежелательно в силу следующих последствий: затрудняется интерпретация параметров множественной регрессии; оценки параметров не надежны.

Наиболее широкое применение получили следующие методы построения уравнения множественной регрессии: метод исключения; метод включения; шаговый регрессионный анализ. Каждый из этих методов по-своему решает проблему отбора факторов и дает, в целом, близкие результаты – отсев факторов из полного его набора (метод исключения), дополнительное введение фактора (метод включения), исключение ранее введенного фактора (шаговый регрессионный анализ или метод включения-исключения). В целом, данные методы называют методами пошаговой регрессии.

Матрица частных коэффициентов корреляции наиболее широко используется в процедуре отсева факторов. При отборе факторов рекомендуется пользоваться следующим правилом: число включаемых факторов обычно в 6-7 раз меньше объема совокупности, по которой строится регрессия.

Литература:О.:11 (гл.5,с.281-297); 9 (гл. 17.4 с.326-329).

Д.: 6 (с.146-152)18 (гл.4 с.52-92); 17 (гл.6 с.157-187); 9 (гл.5 с.189-231, с.276-282)

Контрольные вопросы:

1. Назовите цель прогнозирования экономической системы.

2. Программное обеспечение статистического анализа.

3. Какие виды статистических оценок вы можете перечислить?

4. Какие требования предъявляются к статистическим оценкам параметров распределения?

5. Дайте определение ковариации и опишите метод моментов.

6. Дайте определение ассиметрии и эксцесса, укажите формулы расчета данных показателей.

7. Дайте определение множественной регрессии, анализ ее коэффициентов.

8. Дайте определение парной регрессии, анализ ее коэффициентов.

9. Особенности применения линейной и нелинейной регрессии.

10. Дайте определение коэффициента корреляции, укажите формулу расчета данного показателя.

11. Назовите разницу между линейной и функциональной связью.

12. Назовите и отразите модели нелинейной регрессии.

Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: Сдача сессии и защита диплома — страшная бессонница, которая потом кажется страшным сном. 8860 — | 7189 — или читать все.

193.124.117.139 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.

Отключите adBlock!
и обновите страницу (F5)
очень нужно

источник