Традиционно в американской модели принято выделять комбинацию 4Р, на которую стоит опираться бизнесу. Система 4Р означает «product, price, place, promotion» — продукт, цена, место, и продвижение. Однако, существует ещё одна система 4С, которая более ориентирована на потребителя, и состоит из четырёх переменных:
- Потребитель (Consumer);
- Стоимость (Cost);
- Коммуникация (Communication);
- Удобство (Convenience).
По сути 4Р и 4С системы – это две стороны одной медали, при этом один оценивает перспективы покупателя, а другой продавца. Кстати, стоит отметить, что в 4С модели есть два подхода. Первый был озвучен в 2009 году американскими исследователями маркетинга Джоном Фахи и Дэвидом Джоббером, которые представили систему 4С в виде сочетания таких факторов, как ясность, доверие, последовательность и конкурентоспособность (clarity, credibility, consistency and competitiveness).
Другой, более старый 4С-подход принадлежит американскому профессору рекламы Бобу Лаутерборну, который сформировал его в 1990 году. Он заключался в вышеописанных факторах – потребитель, стоимость, коммуникация и удобство.
Сосредотачивая своё внимание на потребителе, 4С-система делает шаг в сторону от традиционной маркетинговой концепции. В массовом маркетинге (mass-marketing), где предложение одного товара массового производства идёт всему рынку сразу, нет сосредоточения на том, что клиент хочет от продукта. В отличие от сегментированного маркетинга (niche-marketing), которое нацелено на диалог с клиентом, чтобы понять кто он такой, и каковы его реальные потребности. Поэтому для сегментированного маркетинга важны подробные маркетинговые исследования рынка, чтобы определить те ниши, которые не изобилуют конкуренцией, и могут в итоге оказаться прибыльными.
Суть в том, чтобы понять, что клиент хочет покупать. Для маркетологов, проводящих исследование, это должно быть проблемой №1. Ввиду того, что продукт в любой маркетинговой деятельности – это основа, согласно системе 4С, он должен быть продуман досконально, и иметь что-то уникальное, что отличает его от продуктов конкурентов. Самый эффективный способ достижения этого – поиск незанятой ниши, и дальнейшая разработка продукта.
Дифференцированная стоимость даёт значительно лучшую информацию о клиенте, чем дифференцированная цена. Цена – это сумма денег, которую потребитель готов заплатить, чтобы приобрести товар или услугу. Стоимость представляет собой всю совокупность затрат, которые идут на производство товаров или услуг. В плане удовлетворения потребителей, цена является одним из наиболее важных факторов. При этом, она не является главным мотивом при покупке продукта, вопреки распространённому мнению маркетологов. На этапе позиционирования товара или продукта, она может обеспечить относительный успех, но это один из наименее удачных ходов, когда речь идёт о долгосрочной перспективе.
Согласно стратегии 4С Лаутерборна, продвижение – манипулятивный фактор, который управляется только продавцом товара, а не покупателем. В то время, как правильная схема заключается в совместной деятельности покупателя и продавца. Коммуникация должна работать в направлении создания значимых отношений с клиентом, с акцентом на то, в чём они нуждаются, каков их стиль жизни и т. д. Суть в том, чтобы расширять коммуникации с клиентом, располагая их продукту компании, заслуживая их лояльность. Это сможет помочь компании понять свой собственный рынок лучше, и, в конечном счёте, повысить продажи.
Распространение онлайн-рыночных ниш, кредитных карт, онлайн-каталогов, и, наконец, мобильных телефонов дало компаниям ряд больших преимуществ. Сегодня клиент может вовсе не посещать магазин, а совершить покупки онлайн. Есть бесконечное разнообразие мест, где он может это сделать. Это означает, что маркетолог должен знать о том, какова конкретная доля клиентов, которая любит делать покупки таким образом, и сделать в итоге, процесс покупки максимально удобным.
Для владельцев малого бизнеса, система 4С может дать массу преимуществ в привлечении клиентов и покупателей, если использовать её должным образом. Модель 4С также помогает малому бизнесу «взять курс» на более крупных конкурентов. Ключевой момент – выявить целевого потребителя и понять, что он хочет. Для этого необходимо проведение ряда маркетинговых исследований. Следующий шаг – создание именно того продукта, который отвечает всем требованиям целевой аудитории. Это в конечном результате и приведёт к увеличению продаж.
Существует один из самых простых способов использования системы 4С — следование определённому шаблону. Компания должна ответить на вопросы о каждой из составляющих системы 4С:
- Что является конкурентным преимуществом товара или услуги?
- Кто целевые клиенты компании?
- Каковы их потребности и желания?
- Какой продукт или услуга ценен для потребителя?
- Управляет ли клиент решениями?
- Какую цену устанавливает компания для привлечения покупателя?
- Какие проводились маркетинговые исследования, для того, чтобы доказать адекватность этой суммы (насколько, и чем оправдана установленная цена)?
- Доступна ли эта цена для существующих пользователей (для каких категорий)?
- Выгоден ли этот ценовой показатель для компании?
- Какова полная стоимость расходов, которые понесут клиенты, приобретая товары?
- Какие иные аспекты кроме цены могут подвигнуть клиента купить продукт?
- Является ли стоимость достаточной для того, чтобы покрыть все расходы?
- Есть ли план информационной работы, для обеспечения конструктивного диалога с клиентами?
- Имеется ли связь между коммуникациями с клиентами и продажами?
- Можно ли в результате диалога с клиентами ответить на их главные вопросы о продукте, такие как «Что есть в этом товаре хорошего для меня?», «Почему я должен его купить?» и т. д.
- Имеется ли медиа-стратегия продвижения товара в СМИ?
- Каковы потенциальные барьеры, с которыми клиент может столкнуться при покупке товаров или услуг?
- Каковы планы по удалению этих барьеров?
- Имеет ли компания понятный и удобный в навигации веб-сайт?
- Оптимизирован ли он для мобильного использования?
- Если продажи ведутся в Интернете, являются ли условия заказа, оплаты и доставки продукции интуитивно понятными?
- По скольким каналам можно приобрести продукт?
- Достаточна ли поддержка клиентов в компании?
Так, например, в отношении компаний, ведущих продажи в Интернете, весь контент должен быть направлен на потребителя. С практической точки зрения, аудитория будет больше обращаться именно к содержанию. Так, например, компании осуществляющие продажи одежды, должны располагать клиентов – давать практические советы стилистов, рассказывать о существующих тенденциях и т. д. Этот подход помогает строить долгосрочные отношения с потребителями, удерживать их, и постоянно возвращаться к продукту их к компании, превращая в итоге, покупателей в сторонников бренда.
Она включает в себя не только стоимость в денежном выражении, но и стоимость (а также значимость) использования продукта. Пример можно привести в части контент-маркетинга, где содержание должно быть удобным, и если это возможно, экономически эффективным, макеты – привлекающими внимание и т. д.
Интернет сегодня позволяет создавать самые разные каналы связи со своей целевой аудиторией. От Instagramm для фотографий, Twitter для делового продвижения, You Tube для видео, к Facebook, ВКонтакте и т. д. для распространения по страницам пользователей. Сегодня возможности создания новых коммуникаций постоянно увеличиваются.
В этом смысле многое зависит о того, как потребитель будет получать свой товар, или, на примере, с веб-сайтом, то, как он будет считывать содержимое. Нужно определиться с тем, что ему мешает – большое количество всплывающих окон, избыток рекламы, отсутствие оптимизации для мобильного устройства и т. д. Информация должна быть хорошо доступной — через несколько каналов, таких как электронная почта, информационные бюллетени и многое другое.
источник
Значения экономических переменных определяются обычно влиянием не одного, а нескольких объясняющих факторов. В таком случае зависимость Y=f(X) означается, что X – вектор, содержащий m компонентов: X=(X1, X2, … , Xm). Задача оценки статистической взаимосвязи переменных Y и X=(X1, X2, … , Xm) формулируется аналогично случаю парной регрессии.
Связь между зависимой переменной Y и m независимыми факторами можно охарактеризовать функцией регрессии Y=f(X1, X2, … , Xm), которая показывает, каким будет в среднем значение переменной Y, если переменные X примут конкретное значение. Это обстоятельство позволяет применять модель регрессии не только для анализа, но и для прогнозирования.
Множественная корреляция и регрессия определяют форму связи переменных, выявляют тесноту их связи и устанавливают влияние отдельных факторов.
Основными этапами построения регрессионной модели являются:
· отбор факторов для модели, сбор и предварительный анализ исходных данных;
· выбор вида модели и численная оценка ее параметров;
· оценка влияния отдельных факторов на основе модели;
· прогнозирование на основе модели регрессии;
Рассмотрим содержание этих этапов и их реализацию.
2.2.2. Отбор факторов для модели. Сбор и предварительный анализ данных
Информационной базой регрессионного анализа являются многомерные временные ряды, каждый из которых отражает динамику одной переменной и должен удовлетворять изложенным выше требованиям статистического аппарата исследования.
Выбор факторов, влияющих на исследуемый показатель, производится прежде всего исходя из содержательного экономического анализа.
Для получения надежных оценок в модель не следует включать слишком много факторов. Их число не должно превышать одной трети объема имеющихся данных (т.е. m
Коэффициент множественной корреляции, который принимает значение от 0 до 1, более универсальный: чем ближе его значение к 1, тем в большей степени учтены факторы, влияющие на зависимую переменную, тем более точной может быть модель.
Рассмотренные показатели во многих случаях не дают однозначного ответа на вопрос о наборе факторов. Поэтому в практической работе с использованием ПЭВМ чаще осуществляется отбор факторов непосредственно в ходе построения модели методом пошаговой регрессии.
Суть метода состоит в последовательном включении факторов. На первом шаге строится однофакторная модель с фактором, имеющим максимальный коэффициент парной корреляции с результативным признаком. Вычисляется необъясненная дисперсия. Вторым в модель включается фактор с максимальным среди оставшихся факторов коэффициентом корреляции. В результате включения нового фактора в модель снижается необъясненная дисперсия. Дальнейшее включение в модель все большего числа факторов, проранжированных по убыванию коэффициента корреляции с результирующим признаком, ведет к постоянному снижению доли необъясненной факторами дисперсии.
При включении новой переменной в модель рассчитывается величина C(j), равная относительному уменьшению суммы квадратов отклонений зависимой переменной от фактически наблюденных значений, возникающему за счет включения нового фактора в модель.
Величина C(j) интерпретируется как доля оставшейся дисперсии независимой переменной, которую объясняет зависимая переменная j.
Остаточной дисперсией называется та часть вариации зависимой переменной, которую нельзя объяснить воздействием объясняющих переменных (факторов). Именно поэтому она используется как для оценки качества модели и ее точности, так и для полноты набора объясняющих переменных (факторов).
Пусть на очередном шаге к номер переменной, включаемой в модель, соответствует j. Если Скменьше заранее заданной константы, характеризующей уровень отбора, то построение модели прекращается. В противном случае к-тая переменная вводится в модель.
2.2.3. Выбор вида модели и оценка ее параметров
Для отображения зависимости переменных могут использоваться показательная, параболическая и многие другие функции. Однако в практической работе наибольшее распространение получили модели линейной зависимости, т.е. когда факторы входят в модель линейно.
Линейная модель множественной регрессии, которая строится на основе временных рядов наблюдений, имеет вид:
(20)
где Y(t) – зависимая переменная (основной показатель);
Х(t) – независимые переменные (факторы);
t – порядковый номер наблюдения временного ряда (t=1,2…N);
a(j) – коэффициенты регрессии (j=0…m), подлежащие численному оцениванию на основе N наблюдений и m факторов;
E(t) – остаточная компонента, дисперсия которой также должна быть оценена.
Параметры модели оцениваются по МНК. Для двухпараметрической модели система нормальных уравнений, из которой определяются коэффициенты регрессии, имеет вид:
(21)
Здесь и далее суммирование ведется по числу наблюдений N.
Эту систему с тремя неизвестными коэффициентами регрессии можно решить методом Гаусса, по формулам Крамера или любым другим способом.
Если записать выражение для определения коэффициентов регрессии в матричной форме, то становится очевидным, что решение задачи возможно лишь тогда, когда столбцы и строки матрицы исходных данных независимы. Для экономических показателей это условие выполняется не всегда. Линейная или близкая к ней связь между факторами называется коллиниарностью и приводит к линейной зависимости нормальных уравнений, что делает вычисление параметров либо невозможным, либо затрудняет содержательную интерпретацию параметров модели. Чтобы избавиться от коллиниарности, в модель включают лишь один из линейно связанных между собой факторов, причем тот, который в большей степени связан с зависимой переменной.
2.2.4. Проверка качества модели
Качество модели оценивается стандартным для математических моделей образом: по адекватности и точности. Расчетные значения получаются путем подстановки в модель фактических значений всех включенных факторов.
Для проверки адекватности модели регрессии используется F-значение, вычисляемое как отношение дисперсии исходного ряда и несмещенной дисперсии остаточной компоненты. Если расчетное значение с и степенями свободы больше табличного при заданном уровне значимости, то модель считается адекватной.
В качестве меры точности применяют несмещенную оценку дисперсии остаточной компоненты, которая представляет собой отношение суммы квадратов уровней остаточной компоненты к величине . Квадратный корень из этой величины (Se) называется стандартной ошибкой оценки.
(22)
О тесноте связи факторов в модели, а также ее точности, можно судить по величине таких характеристик, как корреляционное отношение, индекс корреляции, коэффициент детерминации.
Так, коэффициент детерминации показывает долю вариации результативного признака, находящегося под воздействием изучаемых факторов, т.е. определяет, какая доля вариации признака Y учтена в модели и обусловлена влиянием на него факторов. Чем ближе этот коэффициент к 1, тем точнее построенная модель.
Целесообразно проанализировать также значимость отдельных коэффициентов регрессии. Это осуществляется по t – статистике путем проверки гипотезы о равенстве нулю к-го параметра уравнения (кроме свободного члена):
(23)
где S(к) – это стандартное (среднеквадратическое) отклонение коэффициента уравнения регрессии а(к).
Если расчетное значение t – критерия с степенями свободы превосходит его табличное значение при заданном уровне значимости, коэффициент регрессии считается значимым. В противном случае фактор, соответствующий этому коэффициенту, следует исключить из модели (при этом ее качество не ухудшится).
2.2.5. Оценка влияния отдельных факторов на основе модели
Важную роль при оценке влияния факторов играют коэффициенты регрессионной модели. Однако непосредственно с их помощью нельзя сопоставить факторы по степени их влияния на зависимую переменную из-за различия единиц измерения и разной степени колеблемости. Для устранения таких различий при интерпретации применяются средние частные коэффициенты эластичности Э(j) и бета-коэффициенты , которые рассчитываются соответственно по формулам:
(24)
(25)
где S(j) – среднеквадратическое отклонение фактора j.
Коэффициент эластичности показывает, на сколько процентов изменяется зависимая переменная при изменении фактора j на один процент. Однако он не учитывает степень колеблемости факторов.
Бета-коэффициент показывает, на какую часть величины среднего квадратического отклонения меняется среднее значение зависимой переменной с изменением соответствующей независимой переменной на одно среднеквадратическое отклонение при фиксированном на постоянном уровне значении остальных независимых переменных.
Указанные коэффициенты позволяют проранжировать факторы по степени влияния факторов на зависимую переменную.
Долю влияния фактора в суммарном влиянии всех факторов можно оценить по величине дельта-коэффициентов D(j):
, (26)
где r(j) – коэффициент парной корреляции между фактором j(j=I,…m) и зависимой переменной;
. (27)
При корректно проводимом анализе все b-коэффициенты положительны.
2.2.6. Прогнозирование на основе модели регрессии
При использовании построенной модели для прогнозирования делается предположение о сохранении в период прогнозирования существовавших ранее взаимосвязей переменных.
Для прогнозирования зависимой переменной на к шагов вперед необходимо знать прогнозные значения всех входящих в нее факторов. Их оценки могут быть получены на основе временных экстраполяционных моделей или заданы пользователем. Эти оценки подставляются в модель и получаются прогнозные оценки.
Для получения интервального прогноза необходимо определить доверительный интервал.
Для линейной модели регрессии доверительный интервал рассчитывается следующим образом. Оценивается величина отклонения от линии регрессии (обозначим ее U):
(28)
Коэффициент Kp является табличным значением t – статистики Стьюдента при заданном уровне значимости и числа наблюдений. Если исследователь задает уровень вероятности попадания прогнозируемой величины внутрь доверительного интервала, равный 70%, то Kp=1,05. Если 95%, то Kp=1,96, а при 99% — Kp=2,65.
Как видно из формулы (28) величина U прямо пропорционально зависит от точности модели, коэффициента доверительной вероятности Kp, степени удаления прогнозной оценки фактора X от среднего значения и обратно пропорциональна объему наблюдений.
В результате получаем следующий интервал прогноза для шага прогнозирования к:
· верхняя граница прогноза =Y(N+к)+U(к),
· нижняя граница прогноза =Y(N+к)-U(к).
Если построенная регрессионная модель адекватна и прогнозные оценки факторов достаточно надежны, то с выбранной пользователем вероятностью можно утверждать, что при сохранении сложившихся закономерностей развития прогнозируемая величина попадет в интервал, образованный нижней и верхней границами.
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Учись учиться, не учась! 10545 — 

источник
Исследовать зависимость между результатами зимней (Х) и летней (У) сессий.
В таблице приведена средняя оценка, полученная по итогам сессии, а также указана принадлежность студента к группе А или Б.
| № п/п | х | у | Группа |
|---|---|---|---|
| 1 | 3,7 | 4,8 | Б |
| 2 | 3,5 | 3,5 | Б |
| 3 | 4,3 | 5 | Б |
| 4 | 3 | 4 | Б |
| 5 | 4,6 | 4,2 | Б |
| 6 | 4,6 | 4,1 | Б |
| 7 | 3,8 | 4,8 | А |
| 8 | 3,6 | 3,5 | Б |
| 9 | 3,3 | 4,4 | Б |
| 10 | 3,9 | 3 | Б |
| 11 | 4,7 | 3,7 | Б |
| 12 | 4,6 | 4,4 | Б |
| 13 | 4,6 | 3,8 | Б |
| 14 | 3,3 | 3,1 | Б |
| 15 | 4,3 | 3,6 | Б |
| 16 | 3,1 | 4,8 | А |
| 17 | 3,2 | 3 | А |
| 18 | 4,2 | 4,8 | А |
| 19 | 3,3 | 3,4 | Б |
| 20 | 3,5 | 4,2 | А |
1. Построить линейную регрессионную модель У по Х.
2. Проверить значимость коэффициентов уравнения и самого уравнения регрессии.
3. Построить регрессионную модель У по Х с использованием фиктивной переменной «группа».
4. Проверить значимость коэффициентов уравнения и самого уравнения регрессии.
5. Вычислить коэффициенты детерминации для обычной модели и модели с фиктивной переменной.
1. Для расчёта параметров а и b линейной регрессии
необходимо решить систему нормальных уравнений относительно a и b:
Построим таблицу исходных и расчётных данных.
Таблица 1 Расчетные данные для оценки линейной регрессии
| № п/п | х | у | х 2 | у 2 | х*у | 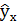 | 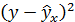 | 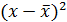 | Группа | z |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 3,7 | 4,8 | 13,69 | 23,04 | 17,76 | 3,973 | 0,684 | 0,024 | Б | 1 |
| 2 | 3,5 | 3,5 | 12,25 | 12,25 | 12,25 | 3,931 | 0,186 | 0,126 | Б | 1 |
| 3 | 4,3 | 5 | 18,49 | 25 | 21,5 | 4,098 | 0,814 | 0,198 | Б | 1 |
| 4 | 3 | 4 | 9 | 16 | 12 | 3,827 | 0,030 | 0,731 | Б | 1 |
| 5 | 4,6 | 4,2 | 21,16 | 17,64 | 19,32 | 4,160 | 0,002 | 0,555 | Б | 1 |
| 6 | 4,6 | 4,1 | 21,16 | 16,81 | 18,86 | 4,160 | 0,004 | 0,555 | Б | 1 |
| 7 | 3,8 | 4,8 | 14,44 | 23,04 | 18,24 | 3,994 | 0,650 | 0,003 | А | |
| 8 | 3,6 | 3,5 | 12,96 | 12,25 | 12,6 | 3,952 | 0,204 | 0,065 | Б | 1 |
| 9 | 3,3 | 4,4 | 10,89 | 19,36 | 14,52 | 3,889 | 0,261 | 0,308 | Б | 1 |
| 10 | 3,9 | 3 | 15,21 | 9 | 11,7 | 4,014 | 1,029 | 0,002 | Б | 1 |
| 11 | 4,7 | 3,7 | 22,09 | 13,69 | 17,39 | 4,181 | 0,232 | 0,714 | Б | 1 |
| 12 | 4,6 | 4,4 | 21,16 | 19,36 | 20,24 | 4,160 | 0,057 | 0,555 | Б | 1 |
| 13 | 4,6 | 3,8 | 21,16 | 14,44 | 17,48 | 4,160 | 0,130 | 0,555 | Б | 1 |
| 14 | 3,3 | 3,1 | 10,89 | 9,61 | 10,23 | 3,889 | 0,623 | 0,308 | Б | 1 |
| 15 | 4,3 | 3,6 | 18,49 | 12,96 | 15,48 | 4,098 | 0,248 | 0,198 | Б | 1 |
| 16 | 3,1 | 4,8 | 9,61 | 23,04 | 14,88 | 3,848 | 0,907 | 0,570 | А | |
| 17 | 3,2 | 3 | 10,24 | 9 | 9,6 | 3,868 | 0,754 | 0,429 | А | |
| 18 | 4,2 | 4,8 | 17,64 | 23,4 | 20,16 | 4,077 | 0,523 | 0,119 | А | |
| 19 | 3,3 | 3,4 | 10,89 | 11,56 | 11,22 | 3,889 | 0,239 | 0,308 | Б | 1 |
| 20 | 3,5 | 4,2 | 12,25 | 17,64 | 14,7 | 3,930 | 0,072 | 0,126 | А | |
| Итого: | 77,1 | 80,1 | 303,67 | 328,73 | 310,13 | 80,1 | 7,649 | 6,45 | х | 15 |
| Среднее: | 3,855 | 4,005 | 15,184 | 16,4365 | 15,5065 | х | х | х | х | х |
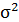 | 0,322 | 0,396 | х | х | х | х | х | х | х | х |
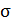 | 0,568 | 0,630 | х | х | х | х | х | х | х | х |
Среднее значение определим по формуле:
Среднее квадратическое отклонение рассчитаем по формуле:
Возведя в квадрат полученное значение, получим дисперсию:
Параметры уравнения можно определить также и по формулам:
Таким образом, уравнение регрессии имеет вид:
Следовательно, с повышением средней оценки, полученной по итогам зимней сессии, на один балл, средняя оценка по итогам летней сессии увеличивается в среднем на 0,2085.
2. Рассчитаем линейный коэффициент парной корреляции:
Связь очень слабая, практически отсутствует.
Определим коэффициент детерминации:
Вариация результата на 3,53% объясняется вариацией фактора х. На долю других, не учтённых в модели факторов, приходится 96,47%. Подставляя в уравнение регрессии фактические значения х, определим теоретические (расчётные) значения 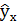
Так как 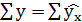
3. Проверим значимость коэффициентов уравнения и самого уравнения регрессии.
Оценку качества уравнения регрессии проведём с помощью F-критерия Фишера.
F-критерий состоит в проверке гипотезы Н о статистической незначимости уравнения регрессии и показателя тесноты связи. Для этого выполняется сравнение фактического Fфакт и критического (табличного) Fтабл значений F-критерия Фишера.
Fфакт определяется по формуле:
где n – число единиц совокупности;
m – число параметров при переменных х.
Таким образом, Н – гипотеза о случайной природе оцениваемых характеристик принимается и признаётся их статистическая незначимость и ненадёжность.
4. Оценку статистической значимости коэффициентов регрессии проведём с помощью t-статистики Стьюдента и путём расчёта доверительного интервала каждого из показателей.
Выдвигаем гипотезу Н о статистически незначимом отличии показателей от нуля: a = b = rxy = 0.
tтабл = 2,1 для числа степеней свободы df = n – 2 = 18 и α = 0,05 .
Фактические значения t-статистики определим по формулам:
t-критерий для коэффициента корреляции можно рассчитать двумя способами:
1)
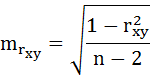
Сравним фактические значения t-статистики с табличными значениями.
Так как фактическое значение t-критерия для коэффициента а превышает табличное, следовательно, гипотезу о несущественности коэффициента а можно отклонить.
Величина t-критерия для коэффициента регрессии меньше табличного и совпадает с величиной tr.
Следовательно, полученная линейная зависимость является недостоверной.
5. По 20 наблюдениям уравнение линейной регрессии (без учёта принадлежности студента к группе А или Б) составило:
Введём в уравнение регрессии фиктивную переменную z для отражения принадлежности студента к группе, а именно: z = 1, для группы Б и z = 0 для группы А. Уравнение регрессии примет вид:
уxz = a + b*x + c*z + ɛ
Применяя метод наименьших квадратов для оценки параметров данного уравнения, получим следующую систему нормальных уравнений:
В виду того, что z принимает лишь два значения (1 и 0), Σz = n1 = 15 (число студентов группы Б), Σх*z =Σх1 =59,3 (сумма х по группе Б), Σz2 =Σz =15, Σy*z =Σy1 =58,5 (сумма у по группе Б).
Тогда система нормальных уравнений примет вид:
Решая её, получим уравнение регрессии:
6. Найдём индекс детерминации для данной модели по формуле:
Добавление в регрессию фиктивной переменной существенно улучшило результат модели: доля объяснённой вариации выросла с 3,53% (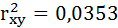
7. Значимость уравнения множественной регрессии в целом, так же как и в парной регрессии, оценивается с помощью F-критерия Фишера:
Так как фактическое значение F-критерия меньше табличного, то уравнение статистически не значимо.
8. Оценка значимости коэффициентов регрессии производится, как и в парной регрессии по t-критерию Стьюдента, по формуле:
где bi – величина параметра регрессии (в наших обозначениях это a, b и с)
a = 3,129; b = 0,335; с = — 0,5516;
Величина t-статистики коэффициентов регрессии b и c меньше табличного tтабл.=2,1 при уровне значимости α 0,05, что свидетельствует о случайной природе взаимосвязи, о статистической ненадёжности всего уравнения.
Таким образом, уравнение в целом незначимо и ненадёжно и не может использоваться в дальнейшем для анализа и прогноза.
источник
Построение и анализ моделей деятельности предприятия относится к области бизнес-консалтинга, включающего в себя построение моделей текущего и целевого состояния предприятия, выработку предложений по совершенствованию его деятельности, формирование целевой программы развития предприятия и плана перехода из текущего состояния в целевое. На данном этапе осуществляется обработка результатов обследования и построение функциональных, информационных и, по необходимости, событийных моделей технологий работы предприятия следующих двух видов.
Модель «как есть»— модель деятельности предприятия, представляющая собой «снимок» положения дел на предприятии на момент обследования. Эта модель включает оргштатную структуру, взаимодействия подразделений, принятые технологии, автоматизированные и неавтоматизированные бизнес-процессы и т.д. Она позволяет понять, что делает и как функционирует данное предприятие с позиций системного анализа, а также, на основе автоматической верификации, выявить ряд ошибок и узких мест и сформулировать ряд предложений по улучшению ситуации;
Модель «как должно быть»— модель будущей деятельности предприятия, интегрирующая перспективные предложения руководства и сотрудников предприятия, экспертов и системных аналитиков по совершенствованию деятельности предприятия.
При этом переход от модели «как есть» к модели «как должно быть» обычно осуществляется одним из двух способов бизнес-реинжиниринга— реорганизации деятельности предприятий.
«Мягкий» реинжиниринг— совершенствование технологий на основе оценки их эффективности. При этом критериями оценки являются стоимостные и временные затраты выполнения бизнес-процессов, дублирование и противоречивость выполнения отдельных задач бизнес-процесса, степень загруженности сотрудников.
«Жесткий» реинжиниринг— радикальное изменение технологий и переосмысление бизнес-процессов. Например, банку, как организации, работу которой нужно реорганизовать, вместо попыток улучшения бизнес-процесса проверки кредитоспособности клиентов, может быть, следует задуматься, а нужна ли вообще такая проверка? Возможно затраты на такие проверки во много раз превышают убытки, которые может понести банк в отдельных случаях некредитоспособности клиента (в случае, когда клиентов много, а суммы сделок незначительны)! Необходимость подобного перехода, собственно, и повлекла за собой создание подходов к реорганизации деятельности предприятий.
В рамках создания, указанных выше, моделей деятельности предприятия должен быть осуществлен:
анализ функциональной деятельности структурных подразделений предприятия;
анализ функционального взаимодействия структурных подразделений;
анализ внутреннего документооборота структурных подразделений;
анализ информационных потоков и информационного взаимодействия структурных подразделений;
анализ применяемых в настоящее время средств автоматизации, как в структурных подразделениях, так и на предприятии в целом.
По результатам анализа и моделирования осуществляется оценка эффективности деятельности структурных подразделении предприятия, на основе которой формируются предложения по совершенствованию его структуры, технологий работы структурных подразделений и предприятия в целом. Критериями такой оценки должны являться:
количество потребителей продукции предприятия;
стоимость издержек производства продукции;
длительность типовых операций производства продукции;
дублирование и противоречивость функций информационных потоков и документооборота;
стоимость и длительность выполнения отдельных шагов технологии или отдельных технологических цепочек шагов;
дублирование и противоречивость выполнения отдельных шагов технологии или отдельных технологических цепочек шагов;
степень загруженности структурных подразделений и должностных лиц;
степень загруженности оборудования, используемого при реализации отдельных шагов технологии или технологических участков;
степень применения средств автоматизации при поддержке выполнения отдельных шагов технологии или отдельных технологических цепочек шагов.
Результатом проведения анализа и оценки являются предложения по совершенствованию деятельности предприятия, а именно:
по изменению технологий целевой и обеспечивающей деятельности предприятия, операций учета, планирования, управления и контроля;
по построению рациональных технологий работы структурных подразделений предприятия с учетом существующих автоматизированных систем;
по созданию перспективной оргштатной структуры предприятия, осуществляющей реализацию рациональных технологий работы;
по изменению информационных потоков и документооборота, обеспечивающих реализацию рациональных технологий работы;
по разработке проектов схем внутреннего и внешнего документооборота, проекта положения о документообороте, проекта альбома форм входных и выходных документов.
На основе разработанных и согласованных предложений формируется целевая программа развития предприятия и план мероприятий по переходу из текущего состояния в целевое. Целевая программа развития предприятия должна включать долгосрочные решения, цели, задачи и основные параметры развития. План мероприятий перехода из текущего состояния в целевое состояние должен содержать:
последовательность, формы, способы и время выполнения задач, поставленных структурным подразделениям предприятия;
распределение сотрудников структурных подразделений и материальных средств по решаемым задачам;
порядок информационного и других видов взаимодействия структурных подразделений и органов управления.
В связи с вышесказанным каждая из моделей деятельности должна включать:
полную функциональную модель с глубиной проработки до уровня конкретного действия должностного лица структурного подразделения предприятия;
информационную модель, интегрированную с функциональной моделью;
динамические, стоимостные, событийные и т.п. модели для осуществления соответствующих оценок.
Ниже перечислены основные виды и последовательность работ, рекомендуемые при построении моделей деятельности.
1) Разработка функциональной модели деятельности предприятия:
определение видов и направлений деятельности;
разработка иерархии диаграмм, образующих функциональную модель деятельности предприятия;
анализ и оптимизация функциональной модели.
2) Разработка модели потоков данных предприятия:
определение информационных потоков между основными процессами деятельности, связей между процессами и внешними объектами;
оценка объемов и интенсивности информационных потоков;
разработка иерархии диаграмм, образующих структурную информационную модель деятельности предприятия;
анализ и оптимизация информационной модели.
3) Разработка информационной модели предприятия:
определение сущностей модели и их атрибутов;
проведение атрибутного анализа и оптимизация сущностей;
идентификация отношений между сущностями и определение типов отношений;
разрешение неспецифических отношений;
анализ и оптимизация информационной модели.
4) Разработка событийной модели предприятия:
идентификация перечня состояний модели и определение возможностей переходов между состояниями;
определение условий, активирующих переходы, и действий, влияющих на дальнейшее поведение;
анализ и оптимизация событийной модели.
Следует отметить, что построенные модели деятельности являются не просто промежуточным результатом, используемым консультантом для выработки каких-либо рекомендаций и заключений. Они представляют собой самостоятельный результат, имеющий большое практическое значение, в частности:
1) Модели позволяют осуществлять автоматизированное и быстрое обучение новых работников конкретному направлению деятельности предприятия (так как ее технология содержится в модели) с использованием диаграмм (известно, что «одна картинка стоит тысячи слов»).
2) С их помощью можно осуществлять предварительное моделирование нового направления деятельности с целью выявления новых потоков данных, взаимодействующих подсистем и бизнес-процессов.
Ниже приводятся некоторые основополагающие рекомендации по структурированию моделей деятельности.
1) Основной принцип заключается в том, что структурирование должно осуществляться в соответствии с видами деятельности и бизнес-процессами предприятия, а не в соответствии с его оргштатной структурой. Именно бизнес-процессы представляют ценность для клиента, и именно их улучшением предстоит в дальнейшем заниматься консультанту. Модель, основанная на оргштатной структуре, может продемонстрировать лишь хаос, царящий в организации (о котором, в принципе, руководству и так известно, иначе оно не воспользовалось бы услугами консультантов), на ее основе, возможно, внести предложения только об изменении этой структуры. С другой стороны, модель, основанная на бизнес-процессах, содержит в себе (не всегда в явном виде) и оргштатную структуру предприятия.
2) Верхний уровень модели должен отражать только контекст системы – взаимодействие единственного процесса, моделирующего контекст предприятия, с внешним миром и ничего более. В случае построения модели структуры, включающей в себя несколько разнотипных предприятий, на контекстном уровне необходимо отразить каждое из этих предприятий и их соответствующие взаимосвязи. Например, контекстная диаграмма горно-обогатительного комбината может содержать процессы автобаза,карьер,фабрикаиуправлениеГОК, контекстная диаграмма регионального банка Сбербанка РФ содержит процессытерриториальноеуправление,типовоеотделение,типовойфилиал.
3) На втором уровне модели должны быть отражены основные виды деятельностипредприятия и их взаимосвязи. Например, для автотранспортного предприятия одним из решений может быть выделение следующих видов деятельности:эксплуатацияавтотранспорта,ремонт и техническое обслуживание,контроль безопасности,управление производством,обеспечивающая деятельность. В случае большого количества видов деятельности некоторые из них можно вынести на третий уровень модели. Такобеспечивающая деятельностьможет включать в себяучет кадров, бухгалтерский учет, экономическое планирование,материально-техническое снабжение, складской учети т.п. Но в любом случае под деятельности необходимо отводить не более двух уровней модели.
4) Каждый вид деятельности, в свою очередь, должна быть детализирован на бизнес-процессы (желательно, единственного уровня). Например, учет кадров включает в себя бизнес-процессы прием на работу,увольнениеи т.п.
5) Дальнейшая детализация бизнес-процессов осуществляется посредством бизнес-функций. Так процесс прием на работусодержит в себе функции прием заявления,оформление приказа,регистрацияи др. Обычно для моделирования бизнес-функции достаточно 2–3 уровней детализации, которая завершается описанием элементарного алгоритма с помощью миниспецификации.
6) Таким образом, общее число уровней в модели не должно превышать 6–7. Практика показывает, что этого вполне достаточно для построения полной модели деятельности современного предприятия любой отрасли.
источник
Модель 4С была разработана специалистами Гарвардской школы бизнеса как средство исследования проблем HRM в рамках более широкой среды бизнеса, чем общепринятые задачи привлечения, отбора, подготовки, аттестации кадров, ведения кадровых записей и проч. В соответствии с Гарвардской моделью (Beer и др., 1985) политика HRM должна строиться на анализе:
Теория заинтересованных лиц
Эта теория предполагает, что поскольку организация принадлежит и управляется различными группами заинтересованных лиц, то задача управления состоит в достижении разумного баланса удовлетворения интересов этих групп. Примером заинтересованных лиц могут служить акционеры, разные категории наемных работников, клиенты и пользователи продукции, кредиторы (в том числе банки), профсоюзы и, возможно, местные или государственные власти. Таким образом, менеджеры должны обладать качествами политиков и дипломатов. Они должны уметь устанавливать хорошие отношения с каждой группой заинтересованных лиц, развивать в себе способности к убеждению, создавать союзы, представлять одну часть заинтересованных лиц другой и проч.
Теория заинтересованных лиц предполагает признание того факта, что каждый групповой интерес имеет право на существование. Так, например, при принятии жизненно важных решений руководство компании должно в равной степени учитывать интересы работников и акционеров.
Заинтересованные лица (выгодополучатели) могут и не занимать формальных постов в компании, хотя все они «инвестировали» что-либо в организацию, будь то их собственный труд, финансовые или иные ресурсы. Поэтому каждое заинтересованное лицо рассчитывает получить вознаграждение от организации и, как правило, стремится оказать влияние на то, как оно определяется. Исходя из этого, руководство должно:
Ситуационные факторы
К числу ситуационных факторов относятся конъюнктура рынка труда, моральные качества и мотивация работников, управленческий стиль (который сам по себе зависит частично от культуры местной общины), используемые на производстве технологии и характер методов работы (например, требуются ли специализация и разделение труда). Критически важной для анализа является конъюнктура рынка труда.
Рынок труда объединяет всех тех, кто ищет работу, и все компании, государственные и прочие организации, которые ищут работников. Рынки труда действуют на региональном уровне, на уровне отрасли хозяйства, на национальном и международном уровнях. Существуют также субрынки для различных категорий занятости, квалификации, образовательного уровня и проч.
Другими ситуационными факторами, которые могут иметь значение, являются:
Ожидания заинтересованных лиц и ситуационные факторы должны приниматься во внимание при разработке стратегии в области человеческих ресурсов и оказывать влияние на политику в области HRM, направленную на решение таких проблем, как система вознаграждения, степень надзора за рабочими, предпочтение применения трудоинтенсивных по сравнению с капиталоинтенсивными методами работы и т. д. Возрастание интенсивности конкуренции в бизнесе может заставить компанию повысить производительность труда, прибегнуть к увольнениям избыточной рабочей силы, реструктуризировать административную систему и т. д. Возрастающие стандарты образования могут привести к соответствующему изменению производственных обязанностей и предоставлению работнику большей самостоятельности.
Последствия для управления человеческими ресурсами
По мнению исследователей из Гарварда, эффективность результатов управления человеческими ресурсами следует оценивать по четырем направлениям (англ. 4С — commitment, competence, congruency, cost-effectiveness):
Проблемы, связанные с моделью 4С
Гарвардская модель предполагает, что политика в области человеческих ресурсов должна быть направлена на повышение уровня каждого С. Например, корпоративная преданность должна усиливаться через совершенствование потока коммуникаций между руководством и наемными работниками, тогда как уровень компетентности должен увеличиваться за счет дополнительной тренировки и обучения. В связи с этом основными проблемами данного подхода являются следующие.
Как точно измерить эти четыре основные переменные.
Вероятность возникновения конфликтов между эффективностью с точки зрения затрат и согласованностью (особенно если стремление к первому означает более низкий заработок).
Огромное разнообразие переменных, потенциально подходящих практически к любой ситуации с человеческими ресурсами. Зачастую просто невозможно выделить ключевые факторы, определяющие настоящий характер конкретной ситуации с человеческими ресурсами.
Признание того факта, что иногда технология или условия работы делают практически невозможным повышение уровня любого из четырех С. Некоторые виды работы неизбежно являются грязными, скучными, повторяющимися, и все равно они должны кем-то выполняться.
источник
Для отбора наиболее значимых факторов xi учитываются следующие условия: 1)связь между результативным признаком и факторным должна быть выше межфакторной связи; 2)связь между факторами должна быть не более 0.7. Если в матрице есть межфакторный коэффициент корреляции rxjxi > 0.7, то в данной модели множественной регрессии существует мультиколлинеарность.;3)при высокой межфакторной связи признака отбираются факторы с меньшим коэффициентом корреляции между ними. 4)Если факторные переменные связаны строгой функциональной зависимостью, то говорят о полной мультиколлинеарности. отбор факторов – 2 этапа –а) логический, выбор зависит от природы взаимосвязи, факторы должны бвть колич измеримы(если необх вкл кач фактор, то придать колич значение), факторы не должны быть интеркоррелированы. Если факторы связаны между собой невозможно определить их влияние на рез-т. при неизменности ост факт если при вкл новых факторов коэфф детерм R 2 не улучшается, а ост дисп не уменьш то нет смысла вкл фактор в модель. Теорет анализ не дает однознач ответа о колич взаимосвязи поэтому:Б)на осн матрицы показ коррел можно искл дублирующие факторы
| rx1y | rx2y |
| rx1y | rx1x2 |
| rx2y | rx1x2 |
Если межфакт rxjxi > 0.7,то факт дублируют друг друга и искл тот факт корр кот при довольно тесн связи с у имеет более слаб связь с др факторами. Матрица пок только явную коллинеарн,чтобы посмотреть мультиколлин необх построить матрицу парных коэфф корреляции, если бы факт не корр между союой то матрица была бы единичной с опред =1, если факт нах в полной лин зависим то опред=0 чем ближе к нулю опред тем больше мультиколл. через коэфф мн детерминации определяется какой фактор ответственнен за мультиколл чем ближе к 1 тем больше .и исключается из модели
15. Мультиколлинеарность факторов и учет ее при построении моделей регрессии.
По величине парных коэфф-тов корреляции обнаруживается явная коллинеарность факторов. Наибольшие трудности в использовании множественной регрессии – при наличии мультиколл факторов, когда более чем 2 фактора связаны между собой линейной зависимостью, т. е. имеет место совок возд факт друг на друга. В рез-те вариация в исходных данных перестает быть полностью независимой, и нельзя оценить воздействие каждого фактора в отдельности. Включение в модель мультиколлинеарных факторов нежелательно в
силу последствий:• затрудняется интерпретация параметров множественной регрессии как
характеристик действия факторов в «чистом» виде, ибо факторы коррелированы;
параметры линейной регрессии теряют экономический смысл;• оценки параметров ненадежны, обнаруживают большие стандартные ошибки и
меняются с изменением объема наблюдений (не только по величине, но и по
знаку), что делает модель непригодной для анализа и прогнозирования.Для оценки мультиколлинеарности факторов может использоваться определитель
матрицы парных коэффициентов корреляции между факторами Если бы факторы не коррелировали между собой, то матрица парных коэффициентов
корреляции между факторами была бы единичной матрицей, поскольку все недиагональные элементы были бы равны нулю. Если же, наоборот, между факторами существует полная линейная зависимость и все коэффициенты корреляции равны единице, то определитель такой матрицы равен нулю. Чем ближе к нулю определитель матрицы межфакторной корреляции, тем сильнее мультиколлинеарность факторов и ненадежнее результаты множественной регрессии, и наоборот. Через коэфф мн детерминации ^2
можно найти факторы ответственные за мультиколлинеарность . чем ближе к 1 тем сильнее мультиколлинеарность сравнивая коэфф можно увидеть переменн отв за мультиколл и исключить их из модели
16. Преодоление мультиколлинеарности при построении модели регрессии.
1)исключение одного или нескольких факторов
2.)преобразование факторов при кот уменьш корр между ними (ряды динамики на ур назад для мскл тенденции) 3)переход к совмещенным уравнениям регрессии те к уравн кот отраж не только связь факт с рез-том но и фзаимод факторов f(x1,x2,x3) y=a+b1x1+b2x2+b3x3+b12x1x2+b13x1x3+b23x2x3+e
Проверить значимость по F взаимод факторов и оставить только значимые 4)переход к уравнениям приведен формы – подстановка рассматр фактора через выраж из др уравнения регресс то есть включит еще одно уравнение где фактор будет рассматр как зависимая переменная.
источник