Статистический метод анализа рисков применяется в случае, когда компания обладает достаточным количеством аналитической и статистической информации относительно объекта анализа
В практике риск-менеджмента наибольшую популярность получили следующие методы анализа рисков:
- статистический;
- оценки целесообразности затрат;
- экспертных оценок;
- аналитический;
- метод использования аналогов;
- оценки финансовой устойчивости и платёжеспособности;
- анализ последствий накопления риска;
- комбинированный метод.
Рассмотрим более детально основные методы анализа рисков и их особенности.
Статистический метод анализа рисков применяется в случае, когда компания обладает достаточным количеством аналитической и статистической информации относительно объекта анализа. Сущность этого метода заключается в том, что для расчёта вероятности возникновения убытков анализируются все исторические данные относительно результативности проведения анализируемых операций компанией в прошлом.
Преимуществом статистического метод анализа рисков является то, что он позволяет осуществлять анализ и оценку различных вариантов развития событий и учитывать различные факторы риска в пределах одного подхода. Недостатком же данного метода является необходимость применения вероятностных характеристик.
На практике используется следующие статистические методы анализа рисков:
- оценка вероятности исполнения;
- анализ вероятного распределения потока платежей;
- деревья решений;
- имитационное моделирование рисков.
Метод оценки вероятности исполнения позволяет дать упрощённую статистическую оценку вероятности исполнения какого-либо решения путём расчёта доли выполненных и невыполненных решений в общей сумме принятых решений.
Метод анализа вероятностных распределений потоков платежей позволяет при известном распределении вероятностей для каждого элемента потока платежей оценить возможные отклонения стоимостей потоков платежей от ожидаемых. Поток с наименьшей вариацией считается менее рискованным.
Деревья решений обычно применяются для анализа рисков событий, имеющих обозримое или разумное число вариантов развития. Они особо полезны в ситуациях, когда решения, принимаемые в тот или иной момент времени, зависят от решений, принятых ранее.
Имитационное моделирование — один из мощнейших методов анализа экономической системы. Под ним понимается процесс проведения на ЭВМ экспериментов с математическими моделями сложных систем реального мира. Имитационное моделирование используется в тех случаях, когда проведение реальных экспериментов, например, с экономическими системами, неразумно, требует значительных затрат и/или не осуществимо на практике. Сбор необходимой информации для принятия решений зачастую требует значительных затрат. В подобных случаях отсутствующие фактические данные заменяются величинами, полученными в процессе имитационного эксперимента.
Сущность метода анализа целесообразности затрат заключается в том, что в процессе деятельности компании затраты каждого направления, а также затраты отдельных элементов имеют разный уровень риска. Определение уровня риска путём анализа целесообразности затрат ориентировано на идентификацию потенциальных зон риска. Это, в свою очередь, предоставляет возможность выявить «узкие» места с точки зрения рисков, а потом разработать пути их ликвидации.
Метод целесообразности затрат позволяет определить критический объём производства или продаж, т.е. нижний предельный размер выпуска продукции, при котором прибыль равна нулю. Производство продукции в объёмах меньше критического приносит только убытки. Критический объём производства необходимо оценивать при освоении новой продукции и при сокращении выпуска продукции, вызванного падением спроса, сокращением поставок материалов и комплектующих изделий, ужесточением экологических требований и другими причинами.
Превышение затрат может быть обусловлено одним из четырёх основных факторов или их комбинацией:
- первоначальной недооценкой стоимости;
- изменением границ проектирования;
- разницей в продуктивности;
- увеличением первоначальной стоимости.
Эти основные факторы могут быть детализированы. На основе типового перечня можно составить детальный контрольный перечень для конкретного проекта или его элементов.
Некоторые исследователи выделяют три показателя финансовой устойчивости фирмы с целью определения уровня риска финансовых средств:
- избыток или недостаток собственных средств;
- избыток или недостаток собственных, средне- и долгосрочных заёмных источников формирования запасов и затрат;
- избыток или недостаток общей величины основных источников для формирования запасов и затрат.
Метод определения уровня риска путём экспертных оценок имеет более субъективный характер (сравнительно с другими методами). Эта субъективность является следствием того, что группа экспертов, осуществляющая анализ риска, высказывает собственные субъективные суждения как о минувшей ситуации (свершившемся событии), так и о перспективах её развития.
Чаще всего метод экспертных оценок применяется при недостаточном объёме информации или при определении уровня риска по таким направлениям деятельности, которые не имеют аналогов.
В обобщённом виде сущность данного метода заключается в том, что компания выделяет определённую группу рисков и рассматривает, как они способны повлиять на её деятельность. Это рассмотрение сводится к выставлению бальных оценок относительно вероятности возникновения того или иного вида риска, а также степени его воздействия на деятельность компании.
Аналитический метод построения кривой риска наиболее сложен, поскольку лежащие в его основе элементы теории игр доступны только очень узким специалистам. Чаще всего используется подвид аналитического метода — анализ чувствительности модели.
Аналитический метод анализа рисков осуществляется в несколько этапов.
На первом этапе осуществляется подготовка к аналитической обработке информации, которая содержит:
- определение ключевого параметра, относительно которого и производится оценка чувствительности (внутренняя норма доходности, чистый приведенный доход и т.п.);
- выбор факторов, которые влияют на деятельность организации и, соответственно, на ключевой параметр (уровень инфляции, состояние экономики и др.);
- расчёт значений ключевого параметра на разных этапах осуществления проекта (закупка сырья, производство, реализация, транспортировка, капитальное строительство и т.п.);
- сформированные таким образом последовательности затрат и поступлений финансовых ресурсов дают возможность определить не только общую экономическую эффективность исследуемого направления деятельности, но и определить её значения на каждой стадии.
На втором этапе строятся диаграммы, отражающие зависимость выбранных результирующих показателей от величины исходных параметров. Сопоставляя между собой полученные диаграммы, можно определить так называемые ключевые показатели, которые оказывают наиболее влияние на оценку доходности проекта.
На третьем этапе определяются критические значения ключевых параметров. Наиболее простым способом при этом является расчёт критической точки или точки безубыточности, отражающей минимально допустимый объём производства продукции или предоставления услуг для покрытия затрат.
На четвёртом этапе, на основании полученных ранее критических значений ключевых параметров и факторов, осуществляется анализ того, оказывают ли на них влияние возможные пути повышения эффективности и стабильности работы организации, т.е. существуют ли пути снижения рисков.
Анализ чувствительности модели. Анализ чувствительности модели состоит из следующих этапов:
- выбор основного ключевого показателя, то есть параметра, по которому и производится оценка чувствительности. Такими показателями могут служить: внутренняя норма доходности, или чистый приведенный доход;
- выбор факторов (уровень инфляции, степень состояния экономики и т.д.);
- расчет значений ключевого показателя на различных этапах осуществления проекта: поиск, проектирование, строительство, монтаж и наладка оборудования, процесс возврата вложенных средств.
Сформированная таким образом последовательность расходов и поступлений даёт возможность определить финансовые потоки для каждого момента времени, то есть определить показатели эффективности.
Сначала строятся диаграммы, отражающие зависимость избранных результирующих показателей от величины исходных параметров. Сопоставляя между собой полученные диаграммы, можно определить ключевые показатели, которые больше всего влияют на оценку проекта.
Затем определяются критические (для проекта) значения ключевых параметров. Проще всего может быть рассчитана «точка безубыточности», отражающая минимально допустимый объём услуг, при котором проект не приносит прибыли, но и не оказывается убыточным.
Если проект финансируется за счёт кредитов, то критическим значением будет и минимальная величина ставки, по которой по проекту не получится погасить задолженность. В дальнейшем может быть получен вариант допустимых значений, в пределах которого проект оказывается эффективным (по доходности) с финансовой и экономической точек зрения.
Анализ чувствительности позволяет специалистам из проектного анализа учитывать риск и неопределённость. Если проект окажется чувствительным к изменению объёма производства продукции проекта, то стоит уделить больше внимания программе обучения персонала и менеджмента, а также другим мерам для повышения производительности.
Вместе с тем анализ чувствительности имеет два серьёзных недостатка:
- он не является всеобъемлющим, потому что не рассчитан для учёта всех возможных обстоятельств;
- он не уточняет вероятность осуществления альтернативных проектов.
источник
показателей эффективности деловой стратегии
Одним из методов количественной оценки риска деловой стратегии является расчет показателей вариации, которые дают представление о том, как отдельные значения показателей эффективности деловой стратегии или ее финансовой реализуемости группируются вокруг среднего значения (насколько они отдалены от средней величины). Вариация показателя эффективности в данном случае — это количественное различие индивидуальных значений этого показателя, полученных при различных сценариях будущего. Чем выше рассеивание показателей эффективности деловой стратегии вокруг среднего значения, тем значительнее степень риска. В рамках данного подхода к оценке риска деловой стратегии можно вместо средней величины выбирать значения базового сценария.
Особенностью исчислений показателей вариации при данном методе является отсутствие вероятностей получения тех или иных значений показателей эффективности. Их изменения определяют специальные показатели:
1) размах вариации, определяемый как разность между наибольшим и наименьшим значениями показателя эффективности:
где хтах — наибольшее значение показателя эффективности; xmin — наименьшее значение показателя эффективности;
2) среднее линейное отклонение d , которое определяется как средняя арифметическая из абсолютных по модулю отклонений индивидуальных значений от средней величины показателя эффективности (или величины базового сценария — базовой величины):
где х — средняя величина показателя эффективности (или показателя эффективности базового сценария);
3) дисперсия (а 2 ) определяется как средняя величина (базовая величина) из отклонений, возведенных в квадрат (х(. -х) ;
4) среднее квадратичное отклонение — корень квадратный из дисперсии:
Помимо абсолютных показателей вариации показателя эффективности, можно рассчитать относительные показатели вариации признака:
• коэффициент осцилляции отражает относительную вариацию крайних значений признака вокруг средней величины:
• относительное линейное отклонение характеризует долю усредненного значения абсолютных отклонений от средней величины:
• коэффициент вариации как отношение среднего квадратичного отклонения к среднему значению:
Если и больше 33%, то говорят о большой вариации признака в изучаемой совокупности.
Рассмотрим пример. Пусть известны значения интегрального экономического эффекта двух стратегий для трех сценариев: оптимистичного, базового и пессимистичного (табл. 4.5).
Интегральный экономический эффект деловой стратегии для трех сценариев, млн руб.
Интегральный экономический эффект
В табл. 4.6 сведем результаты расчетов показателей вариации.
Показатели вариации стратегий
Среднее линейное отклонение, млн руб.
Среднее квадратичное отклонение, млн руб.
Относительное линейное отклонение
Из табл. 4.6 по рассчитанным показателям вариации интегрального экономического эффекта можно сделать вывод о том, что вторая стратегия имеет более высокий уровень риска.
Метод оценки риска, основанный на расчете ожидаемых значений эффективности
Риск представляет собой вероятностную категорию, поэтому в процессе количественного анализа степени риска можно использовать аппарат теории вероятностей и математической статистики. Как известно, главными инструментами оценки риска с использованием теории вероятностей являются следующие показатели:
- • математическое ожидание случайной величины (х);
- • дисперсия случайной величины (/));
- • среднеквадратическое отклонение случайной величины (а).
Математическое ожидание представляет собой обобщенную количественную характеристику случайной величины (ожидаемого показателя) и для ограниченного числа (п) возможных значений случайной величин определяется из выражения
где х. — значение случайной величины;
р — вероятность проявления случайной величины.
Дисперсия характеризует меру изменчивости значений случайной величины и представляет собой средневзвешенное из квадратов отклонений наблюдаемых значений случайной величины от среднего (математического ожидания), которое находится из выражения
Близко связанное с дисперсией среднеквадратическое отклонение определяется из выражения
Дисперсия и среднеквадратическое отклонение служат мерами абсолютного рассеяния значений случайной величины и измеряются в тех же физических единицах, в каких измеряется случайная величина.
Если известны вероятности реализации сценариев, то вариационный метод можно дополнить вероятностной составляющей. Наличие различных сценариев будущего и соответствующих показателей эффективности позволяет говорить об этих показателях как о случайных величинах, то есть величинах, которые могут принимать то или иное значение, но неизвестно заранее, какое именно. Таким образом, известен закон распределения показателей эффективности (как случайных величин). Характер и тип закона распределения отражает общие условия, вытекающие из сущности показателя.
На основании закона распределения можно получить обобщающие характеристики случайных величин, которые измеряют их колебания. Чем эти колебания больше, тем выше рассеивание этих показателей вокруг среднего (или базового) значения и, следовательно, значительнее степень риска стратегии.
Рассмотрим пример. Пусть имеется две стратегии, для которых рассчитан интегральный экономический эффект при реализации трех сценариев. При этом известны вероятности осуществления всех трех сценариев. Исходные данные и расчет обобщающих характеристик представлены в табл. 4.7.
Интегральный экономический эффект стратегий при реализации трех сценариев и обобщающие характеристики
среднее квадратичное отклонение
Несмотря на то, что ожидаемое значение интегрального экономического эффекта первой стратегии больше, то есть она эффективнее, среднее квадратичное отклонение больше, то есть стратегия более рискованна.
Если бы критерием целесообразности стратегии была только величина риска, то первая стратегия была бы предпочтительнее. Поэтому если стратег не склонен к риску, то он может отказаться от более эффективной стратегии в пользу менее эффективной, но и менее рискованной.
В случае, когда какая-либо информация о вероятностях сценариев отсутствует (известно, что в сумме они составляют единицу), расчет ожидаемого интегрального экономического эффекта (ИЭЭо) можно осуществить по формуле
где ИЭЭ_ и ИЭЭ . — наибольший и наименьший ИЭЭ при раз-
X — специальный норматив для учета неопределенности ИЭЭ, отражающий систему предпочтений стратега в условиях неопределенности.
Кроме дисперсии и среднего квадратического отклонения, можно рассчитать дополнительные показатели, характеризующие риск стратегии. Эти показатели рассчитываются по аналогии с показателями для инвестиционных проектов, так как в обоих случаях речь идет об оценке риска на основе показателей эффективности. Чем выше данные показатели, тем риск стратегии больше. К этим показателям можно отнести:
• риск неэффективности стратегии (Рнэ) — суммарная вероятность сценариев, в которых ИЭЭ становится отрицательным:
где Pj — вероятность реализации у’-го сценария, в котором ИЭЭ стратегии отрицателен;
• средний (ожидаемый) ущерб от реализации стратегии в случае его неэффективности (Уэ) определяется по формуле
где |ИЭЭУ| — интегральный экономический эффект при реализации у-го сценария (взятый по модулю).
Метод оценки риска, учитывающий корреляционную зависимость между показателем эффективности и факторными показателями
Факторные связи между изучаемыми показателями можно рассматривать как функциональные и корреляционные. При функциональной связи изменение результативного признака у полностью обусловлено действием другого факторного признака х: у = /(х). При корреляционной связи изменение результативного признака у обусловлено влиянием факторного признаках не полностью, а лишь частично, то есть возможно влияние прочих факторов П: у = /(х) + Q.
По своему характеру корреляционные связи — это связи относительные, они не являются полными (жесткими) зависимостями. Здесь при одном и том же значении факторного признака возможны различные значения результативного признака, что обусловлено наличием других факторов.
В стратегическом менеджменте речь идет о будущем, поэтому корреляционная связь определяется по статистическим (по сути, прошлым) данным. Кроме того, не для всех показателей можно определить корреляционную связь, например из-за отсутствия статистической информации или из-за трудностей ее обработки. Поэтому в целях стратегического менеджмента может допускаться и экспертная оценка корреляционной зависимости. Эта субъективная экспертная оценка будет использоваться в процессе корреляционного анализа в отношении других анализируемых объектов, позволяющего определить наличие и тесноту связи между показателями, и регрессионного анализа, позволяющего установить форму связи и рассчитать аналитическую функцию связи (получить уравнение регрессии).
Наличие и теснота корреляционной связи между факторным и результативным признаками может быть проверена с помощью различных коэффициентов: ассоциации, Пирсона, Спирмэна, корреляционного отношения, индекса корреляции и других. В предположении, что связь между показателями носит линейный характер, используется коэффициент корреляции гху , который рассчитывается по формуле
где х , уп —выборочные (наблюдаемые) значения изучаемых показателей х и у;
N — общее число наблюдений над показателями;
— средние значения показателей.
Значения коэффициента корреляции всегда находятся в промежутке от минус 1 до 1. Для независимых показателей он равен или близок 0. При наличии тесной связи, обуславливающей рост одного показателя при росте другого, он близок к единице. Если рост одного показателя ведет к снижению другого, коэффициент корреляции близок к минус 1. Несмотря на то, что коэффициент корреляции показывает тесноту линейной корреляционной зависимости, на практике при анализе экономических показателей его можно использовать как индикатор наличия или отсутствия любой формы связи.
На основании найденной корреляционной связи между показателем эффективности (результирующий показатель) и факторами, отрицательным образом влияющими на него (факторные негативные показатели), можно сделать вывод о том, что чем больше корреляционная связь между негативным признаком и показателем эффективности, тем риск влияния данного фактора больше. Другими словами, из всей совокупности негативных факторов, то есть факторов, отрицательным образом влияющих на эффективность (снижающих эффективность), носителем риска являются только те факторы, которые имеют высокую корреляционную (отрицательную корреляционную) зависимость. Поэтому в целях оценки риска стратегии в дополнение к корреляционному анализу регрессионный анализ осуществляется в отношении тех показателей, для которых характерна высокая корреляционная зависимость. Это позволит построить регрессионные функции зависимости эффективности стратегии от основных негативных факторов и по ним оценить возможный риск стратегии.
Для оценки риска деловой стратегии важно понимать влияние изменения экономических показателей на ее эффективность, поэтому можно использовать подходы к количественной оценке риска, учитывающие корреляционную зависимость между показателями.
Одним из таких подходов предполагает соотносить риск с относительным снижением эффективности (бЭф^) в результате возможного негативного изменения факторного показателя, от которого эффективность зависит линейно. Коэффициент риска будет определяться по формуле
где ДЭф — отрицательный абсолютный прирост экономического эффекта в результате наступления рискового события, предполагающего негативное изменение всех факторных показателей (берется по модулю), руб.;
Эф — величина экономического эффекта стратегии; ц)э — среднее значение коэффициента корреляции, которое находится как среднее геометрическое по формуле (отрицательные коэффициенты корреляции берутся по модулю)
В формуле (4.3) кроме значений экономического эффекта могут использоваться показатели эффективности. Преимуществами данного подхода к количественной оценке риска являются отсутствие вероятностной составляющей предлагаемого коэффициента риска и учет влияния факторных показателей (как правило, факторов внешней среды) на эффективность деятельности организации.
Рассмотрим пример. Имеются следующие данные по текущим (до реализации стратегии) значениям и будущим (после реализации стратегии) значениям экономических показателей (цена, себестоимость, качество), а также коэффициент корреляции между эффективностью и факторными показателями, которые приведены в табл. 4.8. Наибольшая зависимость эффективности наблюдается от цены и себестоимости. Очевидно, что снижение цены вызовет большее снижение эффективности, чем рост себестоимости или снижение качества.
источник
Ожидаемая стоимость полной информации
Платежная матрица
В более сложных ситуациях имеется несколько состояний природы и несколько возможных вариантов для выбора. Тогда полезно обобщить различные возможные денежные последствия в специальную таблицу, называемую платежной матрицей.
Различные возможные состояния природы заносятся в строки, а альтернативные решения, которые могут быть приняты исходя из имеющихся условий — в столбцы.
На практике каждый поставщик мечтает о том, чтобы точно уравновесить спрос и предложение. В этом случае нет потерь и клиенты удовлетворены. Этот идеальный сценарий может стать более реальным, если точно известен уровень спроса. Если бы продавец мороженного точно знала заранее, сколько порций она должна заказать в каждый день, она более успешно торговала бы со своего лотка. Один из способов получить точную информацию о спросе — просить клиентов заранее делать заказ на продукт, как это делают подписчики на печатные издания. Другой вариант определения будущего спроса — попытка проведения маркетингового исследования, чтобы получить информацию о покупательских предпочтениях своих потенциальных клиентов. Подобные попытки несомненно увеличат затраты на ведение бизнеса. Вопрос заключается в том, сколько именно средств может позволить себе владелец данного бизнеса истратить на получение информации об ожидаемом уровне спроса.
Разница между ожидаемой денежной стоимостью в условиях риска и в условиях определенности называется ожидаемой стоимостью полной информации. Это максимально возможный размер средств, которые мы можем потратить на получение полной информации о рыночной конъюнктуре.
Мы рассмотрели сложности принятия решений в условиях, когда мы не можем быть уверены в том, какой из возможный сценариев событий будет иметь место в реальности. Мы научились рассчитывать ожидаемую денежную стоимость различных вариантов сценариев и остановили свой выбор на сценарии, обеспечивающем максимальный размер этой стоимости. Мы также рассчитали ожидаемую стоимость полной информации о рыночной конъюнктуре, что показывает нам, какую максимальную сумму мы можем потратить на уменьшение степени неопределенности относительно будущих событий.
При принятии любого решения (открытие нового дела, заключение сделки купли-продажи, реализация инвестиционного проекта) предпринимательская фирма может нести потери в результате действия непредвиденных факторов или в тех случаях, если влияние факторов, усиливающих предпринимательский риск, оценено неправильно. Поэтому при оценке риска предпринимателя в первую очередь интересует, какова вероятность того, что в результате принятия решения произойдут потери для предпринимательской фирмы, то есть вероятность нежелательного исхода.
Вероятность при этом означает возможность получения определенного результата. Для предпринимателя расчет данного критерия представляет известную трудность, так как вероятность наступления того или иного события зависит не только от природы неопределенных событий, но и от надежд, которые предприниматель возлагает на них. Существует два метода определения вероятности нежелательных событий:
Объективный метод основан на вычислении частоты, с которой тот или иной результат был получен в аналогичных условиях. В этом случае расчет вероятности проводится на основании фактических данных по формуле, приведенной в описании статистического метода оценки риска.
Субъективная вероятность является предположением относительного определенного результата в тех случаях, когда отсутствует информация, достаточная для применения объективного метода. Субъективный метод определения вероятности нежелательного исхода основан на суждении и на личном опыте предпринимателя.
Объективные анализ и оценка рисков включают в себя два направления: качественный анализ и количественную оценку.
1) Качественный анализ риска может быть сравнительно простым. Его главная задача — определить процессы, этапы и работы, при выполнении которых риск возникает, т.е. установить потенциальные зоны риска, после чего идентифицировать все возможные факторы конкретных рисков. Выявление и идентификация всех возможных (доступных) рисков и их факторов имеет важное значение: от “непредсказуемого”, но выявленного риска можно застраховаться, в то же время от риска не выявленного застраховаться невозможно.
2) Количественная оценка, заключающаяся в численном определении размеров отдельных рисков и риска проекта (программы) в целом — проблема довольно сложная, а порой и недоступная. При количественном измерении экономического риска широко используются методы теории вероятностей (вероятность, законы распределения, выборочное наблюдение и др.), статистики (средние, показатели вариации, корреляции и т.п.), математического, экономико-статистического моделирования. Поскольку одной из важнейших задач управления рисками
В настоящее время наиболее распространенными методами количественной оценки степени риска являются:
· Метод использования аналогов
· Метод анализа целесообразности затрат, чувствительности проекта, сценариев
· Аналитический метод
Статистический метод широко применяется в тех случаях, когда при принятии решения менеджер располагает значительным объемом статистической информации о поведении анализируемой системе, экономическом процессе. Как правило, такой метод используется тогда, когда имеется количество наблюдений за изучаемым явлением, достаточное для получения достоверных выводов, а условия его протекания в анализируемом периоде существенно не отличаются от будущих. При использовании этого метода прежде всего определяется математическое ожидание (для экономических явлений – ожидаемая денежная стоимость в виде доходов или убытков) по формуле:
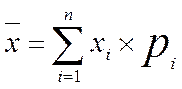
где 

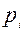
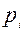

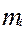

В простых деловых ситуациях, когда принимаемые решения не связаны с о значительными для данного бизнеса суммы, достаточно сравнить затраты с ожидаемой денежной стоимостью результата, а степень риска может быть определена как вероятность получения отрицательного результата (убытка). Вместе с тем математическое ожидание, как средняя величина, представляет собой обобщенную оценку и не позволяет принять правильное решение в пользу какого-либо альтернативного варианта, особенно, когда имеется значительно количество альтернативных решений с близкими средними значениями ожидаемых результатов.
В более сложных случаях степень риска выражается через величину среднеквадратичного отклонения от ожидаемых величин или коэффициент вариации (последний удобен тем, что позволяет сравнивать альтернативные решения).
Среднеквадратическое отклонение определяется по формуле:

Коэффициент вариации показывает относительную меру отклонения отдельных значений от математического ожидания и рассчитывается по формуле:
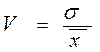
Чем больше коэффициент вариации, тем относительно больший разброс и, соответственно, риск отклонения результата от ожидаемого значения. Изменчивость вариационного ряда, соответственно, и риск принято считать незначительными, если вариация не превышает 0,1, средними – если составляет от 0,11 до 0,25, высокими – если она больше 0,25, но не превышает 0,33. Уровень риска при коэффициенте вариации более 0,33 следует рассматривать как критический. Преимуществом данного метода оценки предпринимательского риска является несложность математических расчетов, а явным недостатком — необходимость большого количества исходных данных (чем больше массив, тем достовернее оценка риска). Статистическим методом невозможно пользоваться, если исследуемый объект — недавно зарегистрированная коммерческая организация или если о ней нет достоверной информации. Следует отметить, что среднеквадратичное отклонение сигнализирует о наличии риска, но при этом скрывает направление отклонения от ожидаемого значения, так как в формуле (2) стоит квадрат разности, а предпринимателю важен знак (+ или -) этого отклонения, для того чтобы знать, что наиболее вероятно — потери или прибыль — в результате совершения данной сделки, проекта и т.п..
Метод использования аналогов используется в том случае, если другие методы оценки риска неприемлемы, но существуют аналоги данной ситуации, решению. При использовании аналогов применяются базы данных о риске аналогичных проектов или сделок. Полученные таким образом данные обрабатываются для выявления зависимостей в завершенных проектах или сделках, с целью учета потенциального риска при реализации нового предпринимательского проекта или сделки. Этот метод обычно используется при анализе рисков новых проектов, которые имеют аналоги, отличающиеся, однако, условиями их реализации от прежних. Для оценки риска этим методом проект рассматривается как “живой” организм , имеющим определенный жизненный цикл. Условия осуществления нового проекта на каждом этапе жизненного цикла сравниваются с условиями уже реализованных аналогов, а отклонения в этих условиях рассматриваются как факторы, изменяющие ожидаемые денежные поступления, их вероятность и изменчивость. После учета этих изменений оценка риска проводится статистическими методами на основании скорректированных данных.
Метод экспертных оценок основан на обобщении мнений опытных специалистов-экспертов о возможных потерях в результате реализации конкретного проекта и вероятности потерь определенного уровня. Интуитивные характеристики, основанные на знаниях и опыте экспертов, дают нередко достаточно точные оценки, во всяком случае, помогают лицам, принимающим окончательные решения, определить с высокой степенью достоверности основные зоны риска оцениваемого проекта, позволяют быстро и без больших временных и трудовых затрат получить информацию для выработки управленческого решения.
Привлеченным к оценке экспертам (желательно работающим независимо друг от друга) предоставляется перечень первичных рисков по всем стадиям жизненного цикла проекта и предлагается оценить вероятность их наступления, руководствуюсь определенной системой оценок. Можно ограничиться получением экспертных оценок вероятностей допустимого критического риска либо оценить наиболее вероятные потери в данном виде предпринимательской деятельности. При этом может применяться, например, следующая система оценок:
25 — рисковая ситуация, вероятнее всего, не наступит;
50 — о возможности рисковой ситуации нельзя сказать ничего определенного;
75 — рисковая ситуация, вероятнее всего, наступит;
100— рисковая ситуация наступит наверняка.
Затем оценки экспертов подвергаются анализу на их противоречивость и должны удовлетворять следующему правилу:
максимально допустимая разница между оценками двух экспертов по любому виду риска не должна превышать 50, что позволяет устранить недопустимые различия в оценках экспертами вероятности наступления отдельного риска.

где 
i — вид оцениваемого риска.
В нашем примере, если три эксперта дали следующие заключения по одному из рисков: эксперт А — 25; эксперт Б — 25; эксперт В — 50, то в данном случае разности оценок составляют: АВ = 0; AC = 25 и ВС = 25, что удовлетворяет условию.
Разновидностью экспертного метода является метод Дельфи. Он характеризуется полной анонимностью и управляемой обратной связью. Анонимность членов комиссии обеспечивается путем физического разделения, что не дает им возможности обсуждать ответы на поставленные вопросы. Цель такого разделения — избежать “ловушек” группового принятия решения, избежать доминирования мнения лидера. После обработки результата через управляемую обратную связь обобщенный результат сообщается каждому члену комиссии. Основная цель этого — позволить ознакомиться с оценками других членов комиссии, не подвергаясь давлению из-за знания того, кто конкретно дал ту или иную оценку. После этого оценка может быть повторена. Данный метод используется различными международными организациями и консалтинговыми фирмами для оценки и выведения рейтингов страновых рисков (в приложении приведено в качестве примера описание рейтингов политического риска для инвесторов, которые рассчитываются Мировым Банком для различных стран).
При экспертной оценке предпринимательского риска большое внимание следует уделять подбору экспертов, так как именно от правильности их оценок зависит решение о выборе того или иного предпринимательского проекта.
Сущность метода анализа целесообразности затрат основывается на том, что в процессе предпринимательской деятельности затраты по каждому конкретному направлению, а также по отдельным элементам, не имеют одинаковую степень риска. Другими словами, степень риска двух разных направлений деятельности одной и той же фирмы неодинакова; и степень риска по отдельным элементам затрат или по отдельным составным риска внутри одного и того же направления деятельности также неодинакова. Так, например, занятие одним видом деятельности фирмы может быть более рискованное по сравнению с другим, и затраты, которые несет диверсифицированная фирма на развитие этих двух направлений своей деятельности, будут также отличаться по степени риска. Такая же ситуация сохраняется и с затратами внутри одного и того же направления. Таким образом, определение степени риска путем анализа целесообразности затрат ориентировано на идентификацию потенциальных зон риска. Такой подход целесообразен еще и с тех позиций, что дает возможность выявить «узкие места» в деятельности предприятия (или “чувствительные параметры проекта) с точки зрения рискованности, а после разработать пути их ликвидации.
При анализе степени риска при помощи использования метода анализа целесообразности затрат рекомендуется использовать градацию затрат на области риска. Для этого состояние по каждому из элементов затрат должно быть разделено на области риска (см. табл. 7.1).
Таблица 7.1 Области деятельности предприятия
| Области деятельности фирмы | Абсолютной устойчи-вости | Нормальной устойчи-вости | Неустойчи-вое состояние | Критическое состояние | Кризисное состояние |
| Области риска | Безрисковая область | область минимального риска | область повышенного риска | область критического риска | область недопустимого риска |
| Максимальные потери | Полное отсутствие потерь | чистая прибыль | расчетная прибыль | валовая прибыль | выручка от реализации и имущество фирмы |
| Коэффи- циент риска | 0-25 | 25-50 | 50-75 | 75-100 |
Эти области представляют собой зону общих потерь, в границах которых конкретные потери не превышают предельного значения установленного уровня риска:
1) область абсолютной устойчивости;
2) область нормальной устойчивости;
3) область неустойчивого состояния;
4) область критического состояния;
5) область кризисного состояния.
В области абсолютной устойчивости степень риска по рассматриваемому элементу затрат соответствует нулевому риску. Данная область характеризуется отсутствием каких-либо потерь при совершении предпринимательской деятельности с гарантированным получением плановой прибыли, размер которой теоретически не ограничен.
Элемент затрат, который находится в области нормальной устойчивости, характеризуется минимальной степенью риска. Для данной области максимальные потери, которые может нести субъект предпринимательской деятельности, не должны превышать границы планируемой чистой прибыли. Таким образом, минимальная степень риска обеспечивает фирме «покрытие» всех ее издержек и получение той части прибыли, которая позволяет покрыть все налоги.
Область неустойчивого состояния характеризуется повышенным риском, при этом уровень потерь не превышает размеры расчетной прибыли (т.е. той части прибыли, которая остается у предприятия после всех выплат в бюджет, уплаты процентов за кредит, штрафов и неустоек). Таким образом, при такой степени риска субъект предпринимательской деятельности рискует тем, что он в худшем случае получит прибыль, величина которой будет меньше ее расчетного уровня, но при этом будет возможность произвести покрытие всех своих издержек.
В границах области критического состояния, которой соответствует критическая степень риска, возможны потери в границах валовой прибыли (т.е. общей сумме прибыли, которая получена предприятием до произведения всех вычетов и отчислений). Такой риск является нежелательным, потому что при этом фирма рискует потерять не просто прибыль, а и не покрыть полностью свои издержки.
Недопустимый риск, который соответствует области кризисного состояния, означает принятие субъектом предпринимательской деятельности такой степени риска, которая предполагает наличие возможности непокрытия всех издержек фирмы, связанных с данным направлением ее деятельности.
После того, как рассчитан коэффициент риска на основании данных прошлых периодов, каждая статья затрат анализируется по отдельности на предмет ее идентификации по областям риска и максимальным потерям. При этом степень риска всего направления предпринимательской деятельности будет соответствовать максимальному значению риска по элементам затрат. Преимущество данного метода состоит в том, что зная статью затрат, у которой риск максимальный, возможно найти пути его снижения (например, в том случае, если максимальная точка риска приходится на затраты, связанные с арендой помещения, то можно отказаться от аренды и купить его и т.п.)
Основной недостаток такого подхода к определению степени риска, так же как и при статистическом методе, состоит в том, что предприятие не анализирует источники происхождения риска, т.е. принимает его как целостную величину, игнорируя его факторы и элементы, его составляющие.
Определенную близость описанному методу (и поэтому могут быть отнесены к данному виду) имеют методы анализа чувствительности проекта, анализа сценариев и “дерева решений”, которые будут рассмотрены ниже на конкретных примерах.
Аналитический или комбинированный метод представляет собой объединение нескольких отдельных методов или их отдельных элементов. Примером может служить оценка предпринимательского риска на основе расчета вероятности нежелательного исхода сделки. В данном случае анализ риска производится с помощью элементов статистического, экспертного методов, а также метода аналога. Таким методом анализируется и оценивается также финансовый риск банкротства предприятия.
Не нашли то, что искали? Воспользуйтесь поиском:
источник
= рассмотреть вероятностный подход к количественной оценке риска;
= изучить сущность и способы расчетов традиционных статистических показателей количественной оценки риска – размах вариации, дисперсия, среднее квадратическое отклонение и размах вариации.
Финансовый риск, как и любой риск, имеет математически выраженную вероятность наступления потери, которая опирается на статистические данные и может быть рассчитана с достаточно высокой точностью.
Эффективность любой финансовой или хозяйственной операции и величина сопутствующего ей риска взаимосвязаны. Также существует взаимосвязь между риском и доходностью рассматриваемого проекта.
Как правило, методы оценки риска и доходности различных инвестиционных проектов производятся для сравнения двух или более проектов, а затем выбора наилучшего или наиболее подходящего для данного инвестора.
Для решения этой задачи надо количественно определить величину финансового риска и сравнить степень риска альтернативных вариантов. Степень риска в большинстве случаев может быть достаточно точно оценена, а так же определена величина доходности предлагаемого проекта, соответствующая данному риску.
Чтобы количественно определить величину финансового риска, необходимо знать все возможные последствия какого-нибудь отдельного действия и вероятность самих последствий. Вероятность означает возможность получения определенного результата.
Применительно к экономическим задачам методы теории вероятности сводятся к определению значений вероятности наступления событий и к выбору из возможных событий самого предпочтительного исходя из наибольшей величины математического ожидания.
Иначе говоря, математическое ожидание какого-либо события равно абсолютной величине этого события, умноженной на вероятность его наступления.
Пример. Имеются два варианта вложения капитала. Установлено, что при вложении капитала в мероприятие А получение прибыли в сумме 15 тыс. руб. — вероятность 0,6; в мероприятие Б получение прибыли в сумме 20 тыс. руб. — вероятность 0,4. Тогда ожидаемое получение прибыли от вложения капитала (т.е. математическое ожидание) составит:
по мероприятию А 15 • 0,6 = 9 тыс. руб.;
по мероприятию Б 20 • 0,4 = 8 тыс. руб.
Вероятность наступления события может быть определена объективным методом или субъективным.
Объективный метод определения вероятности основан на вычислении частоты, с которой происходит данное событие.
Например, если известно, что при вложении капитала в какое-либо мероприятие прибыль в сумме 15 тыс. руб. была получена в 120 случаев из 200, то вероятность получения такой прибыли составляет 0,6 или 60% (120:200).
Субъективный метод базируется на использовании субъективных критериев, которые основываются на различных предположениях. К таким предположениям могут относиться суждение оценивающего, его личный опыт, оценка эксперта, мнение финансового консультанта и т.п.
Величина риска или степень риска измеряется двумя критериями:
1) среднее ожидаемое значение;
2) колеблемость (изменчивость)возможного результата.
Среднее ожидаемое значение — это то значение величины события, которое связано с неопределенной ситуацией. Среднее ожидаемое значение является средневзвешенным для всех возможных результатов, где вероятность каждого результата используется в качестве частоты или веса соответствующего значения. Среднее ожидаемое значение измеряет результат, который мы ожидаем в среднем.
Пример. Если известно, что при вложении капитала в мероприятия А из 120 случаев прибыль 12,5 тыс. руб. была получена в 48 случаях (вероятность 0,4), прибыль 20 тыс. руб. — в 42 случаях (вероятность 0,35) и прибыль 12 тыс. руб. — в 30 случаях (вероятность 0,25), то среднее ожидаемое значение выразилось в 15 тыс. руб.
[(12,5 • 0,4) + (20 • 0,35) + (12 • 0,25)].Изменчивость (колеблемость) возможного результата представляет собой степень отклонения ожидаемого значения от средней величины.
Рисковые активы характеризуются вероятностными значениями получения результата. Если известны все возможные значения результата (здесь имеется в виду значение дохода – в абсолютном выражении или относительная величина – доходность) и вероятности получения этих значений (сумма вероятностей при этом будет равняться единице), то такое представление результата носит название вероятностного распределения.
Вероятностное распределение может быть представлено в виде таблицы или графически. Например, если рассматривается актив А и известны возможные цены его продажи через год, то вероятностное распределение может быть представлено в виде таблицы.
Предположим, что объем инвестиций в данный актив составил 350 денежных единиц. Существует три варианта продажи данного актива:
-за 420 денежных единиц с вероятностью 25%;
-за 400 денежных единиц с вероятностью 50%;
-за 380 денежных единиц с вероятностью 25%.
Рассчитав доход от продажи актива как разность между ценой продажи и инвестированными в него средствами, а также произведя расчет доходности по формуле:
,
получим следующую таблицу:
| Цена продажи | Вероятность | Доход | Доходность |
| 25% | 20% | ||
| 50% | 14,3% | ||
| 25% | 8,6% |
Ожидаемое значение результата определяется как сумма произведений возможных значений результата на соответствующие значения вероятностей.
Исходя из вышеуказанного примера получаем следующее значение ожидаемой доходности:
При предположении о возможности указать вероятность каждого исхода можно построить график непрерывного распределения вероятности. Чем более заостренной будет форма кривой непрерывного распределения вероятности, тем больше вероятность, что фактическая доходность будет ближе к ожидаемому значению и тем ниже риск принимаемого решения.
Во многих исследованиях, включающих оценку вероятности предполагается, что вероятностное распределение является нормальным[2]:
Нормальное распределение вероятностей предполагает, что среднему состоянию доходности соответствует самая большая вероятность (при этом данная величина доходности является одновременно и средним арифметическим двух крайних значений), а далее значения вероятностей равномерно уменьшаются при удалении от нормы как в одну, так и в другую сторону, стремясь к нулю в крайних положениях. Сумма всех вероятностей при этом равна 1.
Нормальное распределение достаточно полно отражает реальную ситуацию и дает возможность, используя ограниченную информацию, получать числовые характеристики, необходимые для оценки степени риска того или иного проекта.
Как было отмечено, количественно риск может быть охарактеризован как некий показатель, измеряющий вариабельность дохода или доходности. Таким образом, для этой цели может быть использован ряд, как относительных, так и абсолютных, статистических коэффициентов. Традиционными в этом плане являются: размах вариации, дисперсия, среднее квадратическое отклонение и коэффициент вариации.
Размах вариации — это разность между максимальным и минимальным значениями признака данного ряда.
Этот показатель имеет много недостатков, основными из них являются:
— этот показатель дает грубую оценку степени вариации значений признака;
— он является абсолютным показателем, и потому его применение в сравнительном анализе весьма ограничено;
— его величина слишком зависит от крайних значений ранжированного ряда.
Считается, что чем выше значение размаха вариации, тем выше степень риска по данному проекту, т.е. наилучшим (под наилучшим подразумевается проект с наименьшей степенью риска) окажется тот проект, у которого значение размаха вариации окажется минимальным.
Дисперсия является средним квадратом отклонений значений признака от его средней величины и рассчитывается по следующей формуле:
,где
— ki – значение доходности по данному активу;
— — среднее, ожидаемое значение доходности, рассчитываемое по формуле: ;
— — вероятность, соответствующая данному значению доходности;
— n – число возможных отклонений от ожидаемого значения.
Дисперсия измеряется в тех же единицах, что и результат — в процентах, если в качестве результата рассматривается доходность, и в денежных единицах, если в качестве результата рассматриваются денежные потоки, но возведенных в квадрат.
Среднее квадратическое отклонение показывает среднее отклонение значений варьирующего признака относительно центра распределения, в данном случае – средней арифметической. Этот показатель рассчитывается по формуле:
, где
— ki – значение доходности по данному активу;
— — среднее, ожидаемое значение доходности, рассчитываемое по формуле: ;
— — вероятность, соответствующая данному значению доходности;
n – число возможных отклонений от ожидаемого значения.
Среднее квадратическое (стандартное) отклонение более удобно, чем дисперсия, так как измеряется в тех же единицах, что и результат, что облегчает сравнение и анализ риска различных активов, в отличие от дисперсии.
Для оценки риска через стандартное отклонение необходимо:
— рассчитать абсолютное отклонение возможных значений доходности от ожидаемого значения;
— возвести в квадрат полученное отклонение;
— домножить квадрат отклонений на соответствующее значение вероятности.
Сумма произведений составит значение дисперсии, после извлечения квадратного корня получим среднее квадратическое отклонение.
Коэффициент вариации – относительная величина, которая рассчитывается по формуле:
, где
— — среднее, ожидаемое значение доходности;
— σ – среднее квадратическое отклонение.
Если сравниваются активы, имеющие различную доходность, то по значению среднего квадратического отклонения нельзя сделать вывод, какой из них является более рискованным.
Для сравнения активов с различной доходностью по степени риска необходимо уравнять разброс с учетом доходности, т.е. рассчитать риск на единицу доходности.
Таким нормированным показателем степени риска являетсякоэффициент вариации, как отношение среднего квадратического отклонения к ожидаемому значению доходности.
Чем выше коэффициент вариации, тем выше риск владения активом. Такое утверждение верно при равной ликвидности рассматриваемых активов.
Такие показатели, как дисперсия и среднее квадратическое отклонение, обладают одним общим недостатком: это абсолютные показатели, значения которых существенно зависят от абсолютных значений исходного признака ряда. Поэтому большее применение имеет коэффициент вариации.
В отношении оценки риска финансовых активов, как отмечалось выше, риск может оцениваться вариабельностью либо дохода либо доходности.
Поскольку доход в абсолютной оценке может существенно варьировать при сравнительном анализе различных финансовых активов, то принято в качестве базисного показателя, характеризующего результативность операции с финансовым активом, использовать не доход, а доходность. Доходность не зависит от размера инвестиции и потому сопоставима в пространственно-временном разрезе.
Также, основными показателями оценки риска на рынке капитала являются дисперсия и среднее квадратическое отклонение. Распространенность и пригодность в сравнительном анализе этих статистик в данном случае объясняется тем обстоятельством, что базисным показателем при расчетах является доходность, т.е. относительный показатель, сопоставимый как в динамике, так и по различным видам активов. Поэтому независимо от анализируемых активов соответствующие им показатели доходности и дисперсии однопорядковы, и нет острой необходимости применять в оценке коэффициент вариации.
При оценке риска используют модификации формул дисперсии и среднего квадратического отклонения, в которых весами значений ожидаемой или требуемой доходности являются вероятности их появления.
Необходимо отметить еще одну очень важную особенность анализа риска и доходности.
Как и любая вероятностная категория, риск может быть оценен по-разному. Однако, речь должна идти не только и не столько о различии алгоритмов и критериев оценки, приведенных выше, сколько о том, рассматривается ли данный финансовый актив изолированно или как составная часть набора активов.
При рассмотрении актива изолированно никаких особых проблем теоретического характера в принципе не возникает, а его рисковость может быть измерена с помощью одного из рассмотренных выше показателей.
Также следует отметить, что наиболее часто варианты доходности по проекту рассматриваются по оптимистическому, нормальному и пессимистическому прогнозам.
Рассмотрим все вышеуказанные показатели на конкретном гипотетическом примере.
В таблицах представлены данные по двум проектам:
| Прогноз | Доходность | Вероятность |
| Оптимистический | 100% | 20% |
| Нормальный | 70% | 50% |
| Пессимистический | 20% | 30% |
| Прогноз | Доходность | Вероятность |
| Оптимистический | 70% | 30% |
| Нормальный | 50% | 40% |
| Пессимистический | 40% | 30% |
Теперь, исходя из имеющихся данных, произведем оценку риска с используя названные методы.
Рассчитаем размах вариации по двум проектам:
По данному показателю наиболее предпочтительным является проект Б, имеющий меньшее значение размаха вариации. Но надо учесть, что данный коэффициент не учитывает вероятность наступления той или иной ситуации, благодаря которой доходность будет изменяться и большую или меньшую сторону.
Рассчитаем значение ожидаемой доходности:
для проекта А: 100*0,2+70*0,5+20*0,3=20+35+6=61%
для проекта Б: 70*0,3+50*0,4+40*0,3=21+20+12=53%.
Рассчитаем значения дисперсии:
| Вероятность | |||
| 0,2 | 100-61=39 | 304,2 | |
| 0,5 | 70-61=9 | 40,5 | |
| 0,3 | 20-61=-41 | 504,3 |
Таким образом, σ 2 =304,2+40,5+504,3=849.
| Вероятность | |||
| 0,3 | 70-53=17 | 86,7 | |
| 0,4 | 50-53=-3 | 3,6 | |
| 0,3 | 40-53=-13 | 50,7 |
Таким образом, σ 2 =86,7+3,6+50,7=141.
В итоге получается, что средний уровень доходности по проекту А выше (61% в отличие от 53% по проекту Б), но в то же время дисперсия, показывающая уровень риска, указывает на то, что проект А является более рисковым, чем проект Б. Таким образом, если бы инвестор ориентировался бы только на уровень доходности, не учитывая фактор риска во время анализа проекта, он выбрал бы проект А, т.к. он наиболее доходный. Но если принимать во внимание значение уровня риска, то инвестор выбрал бы скорее всего проект Б, т.к. степень риска по нему значительно ниже при несущественном уменьшении доходности (всего на 8%, 61%-53%=8%).
Рассчитаем значение среднего квадратического отклонения:
Полученные значения также указывают на то, что уровень риска по проекту Б ниже, чем по проекту А.
И, в заключение, рассчитаем коэффициент вариации:
.
Коэффициент вариации также показывает, что осуществление проекта А является более рискованным, чем осуществление проекта Б.
Следует также отметить, что существуют разные типы инвесторов. Имеются ввиду инвесторы, склонные к риску, и инвесторы, не склонные к риску.
Так, инвесторы, склонные к риску и ориентированные ни максимизацию прибыли при осуществлении своего проекта, скорее всего выберут проект А. Проект же Б покажется более привлекательным второй категории инвесторов, т.е. тем, которые не склонны к риску.
Таким образом, конечный выбор того или иного проекта зависит не только от данных и показателей, полученных в ходе анализа риска и доходности сравниваемых проектов, но и от личности инвестора,т.е. лица, принимающего решения.
Контрольные вопросы, задания и тесты:
1. Какова математическая возможность оценки финансового риска?
2. Что такое математическое ожидание?
3. В чем заключается субъективный подход к оценке финансового риска?
4. Назовите статистические методы оценки финансового риска и дайте их характеристику.
Задание 1. Инвестиционные проекты имеют следующие характеристики:
| Прогноз | Проект А | Проект Б | Проект В | |||
| % | доходность | вероятность | доходность | вероятность | доходность | вероятность |
| оптимистический | ||||||
| нормальный | ||||||
| пессимистический |
Оцените финансовый риск реализации каждого из проектов.
Тест 1. Выберите правильный ответ:
Если сравниваются активы, имеющие различную доходность, то сделать вывод, какой из них является наиболее рискованным по значению стандартного отклонения:
3. требуется дополнительная информация.
4. правильный ответ отсутствует.
Тест 2. Выберите правильный ответ:
Коэффициент вариации – это:
4. правильный ответ отсутствует.
МОДУЛЬ 7. ВЫВОДЫ.
Изучив данный модуль Вы должны понимать сущность финансовых рисков и особенности их реализации на предприятии.
= дать характеристику финансовых рисков;
= раскрыть сущность финансовых рисков с точки зрения принятия на предприятии типа финансового решения;
= дать характеристику, показать компенсационные возможности по финансовым рискам собственников, кредиторов и менеджеров предприятия;
= провести математическую оценку финансового риска.
1. Балабанов И.Т. «Риск-менеджмент», М., «Финансы и статистика», 1996 г.
3. Ковалев В.В. «Финансовый анализ», М., «Финансы и статистика», 2000 г.
4. Ковалев В.В., Ковалев Вит.В. «Финансы предприятий», М., «Проспект», 2002 г.
[1] Финансово-промышленные группы в России: необходимость, сущность, перспективы. — Иркутск, 1999. [2] Теплова Т.В. «Финансовый менеджмент: управление капиталом и инвестициями»Дата добавления: 2015-03-31 ; Просмотров: 1048 ; Нарушение авторских прав? ;
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
источник
