Линейное программирование как метод сравнительного анализа

Среди эмпирических методов исследования определенных событий чаще всего используется метод сравнительного анализа. Благодаря ему выявляются общие и отличные черты (характеристики) какого-либо явления, исследуемого процесса на разных этапах развития (временных, событийных и т. д.).

Сравнительный метод – это один из главенствующих логических приемов познания предметов, явлений, событий внешнего мира, которое начинается с того, что аналитики их отделяют от всех предметов и (или) устанавливают их сходство с родственными предметами и явлениями.

Через сравнение определяются общие и отличные методологические подходы научных школ, которые изучают некие процессы, сравнивают определенные критерии и категории. Причем сравниваются только те явления (характеристики), которые имеют сходные признаки и объективную общность в рамках выбранного научного исследования. В итоге можно выяснить общее, что повторялось в явлениях и стало ступенькой на пути выявления ряда закономерностей изучаемых событий.

Для исследования динамики изменения неких процессов, поиска различий и общностей часто используют сравнительный анализ. Примеры практического использования можно найти в социологии, юриспруденции, политическом и экономическом анализе, науке и культуре.

Общеизвестно, что определять динамику эффективности предприятия удобно не с помощью абстрактных величин, а сравнивая либо с другими схожими фирмами, либо основываясь на статистике компании в равновесный промежуток времени. Например, как изменилась производительность труда (доходы, убытки) в текущем году относительно аналогичного промежутка времени прошлых лет, как за это время сработали предприятия-конкуренты.

Метод сравнительного анализа незаменим в социологии, исследовании общественного мнения, статистическом анализе. Только опираясь на данные предыдущих исследований, можно точно выявить динамику изменения настроений в обществе, оперативно выявлять нарастающие проблемы и вовремя на их реагировать. Сравнительный анализ эффективен и показателен на всех уровнях: от отдельной семьи до всего общества, от бригады до коллектива большого предприятия, от муниципального уровня до государственного.

Виды анализа зависят от методики и количества сравниваемых показателей. При отслеживании определенного явления можно опираться на данные самого явления, сравнивать его с аналогичным либо с совокупностью явлений. Например, при отслеживании динамики хозяйственной деятельности компании можно опираться на ее собственную статистику за различные временные промежутки, сравнивать с конкурирующей фирмой либо оценивать в контексте всей отрасли (совокупности фирм).

• Количественный – анализ с точки зрения количественного представления характеристик.
• Качественный – анализ качественных характеристик, свойств.
• Ретроспективный – анализ изменений во времени, их влияние на текущие события.
• Прикладной – анализируется практическая деятельность исследуемой структуры.
• Исследовательский – применяется в аналитических науках.
• Описательный – анализ начинается с исследований структуры явления, затем идет к его функциям и цели.
• Общий – базируется на общей теории систем.
• Структурный – анализируется общая структура явления.
• Микросистемный – исследуется конкретная система.
• Макросистемный – анализируется роль конкретной системы в совокупности родственных систем.
• Витальный – анализируется развитие системы, определяются ее основные этапы.
• Генетический – используется в анализе генетических систем, механизмов наследования.
• Другие виды.

Сравнительный анализ систем правоведения различных стран позволяет развивающимся государствам перенимать эффективно зарекомендовавшие себя методы управления, совершенствовать законодательство, структуру административной системы.

Изучение теоретического наследия свидетельствует о том, что развитие теории права в одной стране вне контекста всемирной истории и достижений правовой мысли других стран невозможно и приводит к узкому ограниченному подходу в определении проблем права. Именно это, собственно, и определяет закономерность транснациональной природы правовой науки, не исключая при этом социально-политической функции правоведения конкретного государства. Например, даже советская юридическая наука являлась не изолированной системой, а частью диалектически целостной мировой юриспруденции.

Правовой метод сравнительного анализа – это, прежде всего, сопоставление компаративистики, то есть анализ сходных черт. Ряд уважаемых исследователей отмечают два основополагающих условия правильного применения сравнительного метода:

• Не следует ограничиваться сравнением народов одной расы или религии.
• Сравнивать можно только законодательства или правовые системы, находящиеся на одном уровне общественного развития.

Почему? Сравнительная история права не должна ограничиться простым сопоставлением исследуемых юридических систем лишь потому, что они сосуществуют одновременно во времени или территориально близко. Ведь в праве нет места для экспериментов – по каждому решению, направленному на создание или реализацию права, стоят судьбы и интересы граждан, экономики, государства. Право должно быть максимально совершенным и системным. Именно поэтому, вместо эксперимента, используют сравнительно-правовые исследования, которые укажут важные варианты решений, предостерегут от принятия устаревших или неэффективных в актуальных условиях решений.

Задекларированное вхождение страны в мировое сообщество в условиях перехода экономик ведущих стран мира на инновационное развитие заставляет отечественных товаропроизводителей модернизировать производство. Промедление грозит системным отрывом от развитых стран и превращением в сырьевой придаток, донора дешевой рабочей силы. Понимая это, передовые отечественные предприятия пытаются найти свое место на мировом рынке, опираясь на новые разработки.

Однако поиск идей инновационных разработок в основном ведется чисто интуитивным путем, при этом шансы на успех являются незначительными и больше зависят от субъективных факторов. В то же время существует метод сравнительного анализа. Он позволяет:

• Вести целенаправленный поиск идей новых товаров, технологий их изготовления, методов управления.
• Осуществлять выбор наиболее приемлемых идей инноваций, повышая тем самым шансы инвесторов на успех.
• Закладывать основы перехода на инновационное развитие.

Для эффективного хозяйствования сравнительный метод жизненно необходим. Как по-другому отслеживать, лучше стала работать фирма или хуже? Каково ее место на рынке? Как развиваются конкуренты? Только при сравнении с предыдущими временными периодами собственной деятельности и по возможности конкурирующих структур можно строить стратегические планы развития.

При исследовании больших объемов данных здорово помогает таблица сравнительного анализа. Она позволяет наглядно структурировать показатели. Пример простейшей сравнительной таблицы (коэффициенты взяты условно):

источник

Если целевая функция и все ограничения в задаче оптимизации являются линейными функциями, то такая задача носит название линейного программирования. В общем случае она имеет вид:

Если в общей модели присутствуют ограничения 3-х видов, то задачи, в которых есть только ограничения первого вида, не считая ограничений на знаки переменных, называются задачами распределительного типа.

Они широко распространены, поэтому будут подробно рассматриваться в рамках данного курсового проекта.

Понятно, что ограничения определяют область допустимых значений переменных, поэтому любое x из этой области являются допустимым решением, а x* — оптимальное решение, если:

Те ограничения, которые принимают вид равенства, называются активными ограничениями; соответствующий этому ограничению ресурс называется дефицитным.

Стандартная форма записи задачи линейного программирования имеет вид:

Система уравнений является базисной, то есть ранг матрицы равняется L-числу строк. Понятно, что L

Запишем базисную систему в виде:

Поскольку Rang (A_Б) = L, то можно сказать, что матрица существует.

является решением матричного уравнения при любых .

Если , где — N-мерный ноль, то полученное решение называется допустимым. Если при этом , т.е. , то решение называется базисным. Если, к тому же, , то решение называется допустимым базисным.

Если множество не пусто, то область допустимых значений выпукла, и базисные решения существуют.

Также можно показать, что допустимое базисное решение является крайней точкой .

Если замкнута, то число крайних точек ограничено.

Целевая функция достигает своего максимума в крайней точке.

Если же max достигается в нескольких крайних точках, то значение функции в этих точках одинаково. Такое же значение функция принимает во всех точках выпуклой и линейной комбинации этих крайних точек.

То, что целевая функция достигает max в крайней точке, а число таковых ограничено, в принципе, позволяет решить задачу оптимизации простым перебором значений функции в крайних точках.

Однако, число крайних точек растет как N!. Поэтому разработан симплекс-метод, заключающийся в том, что, начиная с базисного решения, осуществляется переход к другим базисам при условии роста значений целевой функции. Симплекс-метод при известном допустимом базисном решении. Для задач распределительного типа, в которых присутствуют ограничения типа несложно убедиться в том, что после записи задачи в стандартной форме легко можно найти допустимые базисные решения, которые можно использовать в качестве начального базиса.

Если в задаче N переменных и L ограничений (), то целевая функция имеет вид:

Разделим Г на 2 части: Г (Г_БГ_S). Тогда целевая функция будет выглядеть как:

В начальной допустимой базисной точке, как известно, Y_S=0. Следовательно,

Идея симплекс-метода заключается в том, что при переходе к новому допустимому базисному решению второе слагаемое должно быть положительным. Среди положительных выбирается наибольшее. В скалярном виде:

Метод выбора столбца, вводимого в базис и выбора строки переменной, выводимой из базиса, сведем в так называемую симплекс-таблицу.

Рассмотрим следующую задачу:

Параметр k в этом случае — подбираемый коэффициент, величина которого оказалась: k=7.

Рассмотрим геометрический способ решения задачи линейного программирования. Запишем для данного случая:

Тогда на рисунке можно увидеть, что область допустимых значений, ограниченная указанными прямыми, принимает вид пятиугольника:

Оптимальное решение соответствует прямой, параллельной f_нач. и проходящей через самую дальнюю от f_нач. точку допустимого множества. Из графика видно, что оптимальная точка x* (1.8, 1.14375) находится на пересечении g1 (x1) и g2 (x2). Значение функции в этой точке: f (x*) =15.375.

Для решения данной задачи с помощью симплекс-таблиц перепишем исходную систему в следующем виде:

Тогда симплекс-таблица на 0-й итерации примет вид:

источник

Линейное программирование представляет собой методы решения определенного класса задач по нахождению крайних значений (шах или min). Они основаны на решении системы линейных уравнений, когда зависимость строго функциональна. В модели линейного программирования выделяются три составные части: целевая (максимизируемая или минимизируемая) функция, система ограничений и условие неотрицательности переменных. Математический аппарат линейного программирования используется при решении задач экономических, технических, военных и др.

В экономических задачах оптимального планирования решение целевой функции сводится к нахождению максимума, например, прибыли, объема производства, производительности труда или минимума текущих затрат, капиталовложений, времени выполнения работ и т.п.

В тоже время надо отметить, что не каждая задача оптимального планирования может быть сформулирована и разрешена в рамках линейного программирования. Для этого необходимо соблюсти четыре основных условия.

• 1. В задаче должен быть четко сформулирован и количественно определен критерий оптимальности, что не так легко сделать на практике. О работе предприятия чаще всего судят по ряду показателей: объему производства, ассортименту и качеству выпускаемой продукции, рентабельности производства и др. Выбор одного критерия может оказаться далеко не лучшим с точки зрения другого и наоборот.
• 2. Важной составной частью задачи линейного программирования являются ограничения, связанные с наличными ресурсами, потребностями или другими факторами. В реальной экономике не всегда можно учесть взаимодействие слишком большого количества факторов, поэтому составляется упрощенная модель, которая бы более близко отражала действительный характер.
• 3. Линейное программирование предполагает выбор вариантов и оно применимо только тогда, когда конкретные условия экономической задачи обусловливают эту свободу выбора.
• 4. Модель должна содержать только линейные уравнения или неравенства, т.е. все переменные задачи должны быть в первой степени. Реальные экономические зависимости не всегда носят линейный характер.

Учитывая соответствующие условия и приближая экономическую ситуацию для решения задач линейного программирования, необходимо также учитывать, что наложение на переменные величины слишком жестких ограничений может привести к противоречивости всей системы исходных условий задачи.

По характеру решаемых задач методы линейного программирования можно разбить на две группы.

• 1. Универсальные методы. С их помощью могут решаться любые задачи линейного программирования. Самым распространенным из них является симплексный метод, предложенный Дж. Данцигом, метод раз- решаюших множителей, разработанный академиком Л. В. Канторовичем в 1939 г., примерно за 10 лет до его появления за рубежом.
• 2. Специальные методы. Эти методы проще универсальных, но применимы не для всех задач. К ним относятся распределительный метод для решения транспортной задачи, метод разрешающих слагаемых А. Л. Лурье, метод дифференциальных рент А. Л. Брудно, венгерский метод.

К особой группе методов линейного программирования относятся приближенные методы, отличающие от остальных тем, что не гарантируют строго оптимального решения задачи, но они просты и хорошо приспособлены к ручным вычислениям. К ним относятся индексный метод, метод аппроксимации Фогеля и др.

Симплексный метод. Чтобы лучше понять идею симплексного метода, рассмотрим решение задачи оптимизации использования ресурсов с целью достижения максимальной прибыли.

Имеется вспомогательное производство, которое использует остающиеся от основного производства материалы. На данном производстве налажен выпуск дверей различного ассортимента: с использованием стекла (ассортимент ЛВС) и без него (ассортимент ДВ). Сбыт данной продукции обеспечен, т.е. продукция может производиться в любых соотношениях, но есть ограничение по количеству рабочих мест в цехе и ресурсам основных материалов. Задача состоит в том, чтобы запланировать цеху ежемесячный выпуск продукции, обеспечивающий наибольшую возможную сумму прибыли.

Нормы затрат на единицу продукции

Прибыль с единицы продукции, тыс. руб

Имеющийся объем ресурсов (в месяц)

В задаче не ставится условия обязательного использования всего объема ресурсов. Необходимо, чтобы расход рабочего времени был не больше заданных пределов.

Рассмотрим программу 1, которая предполагает выпуск только дверей ассортимента ДВ, нс используя при этом стекло для их производства.

Если выпускать только ДВ, используя при этом все имеющиеся ресурсы, то их хватит для выпуска:

• — по рабочему времени: 520/9,2 = 56 (шт.);
• — древесине: 24/0,3 = 80 (шт.).

Следовательно, всех ресурсов достаточно для выпуска только 56 дверей.

Прибыль при данном выпуске составит 168 000 руб. (56 • 3000).

Программа 2 предполагает выпуск только дверей ассортимента ЛВС. В данном случае ресурсов хватит для выпуска:

• — но рабочему времени: 520/4 = 130 (шт.);
• — древесине: 24/0,6 = 40 (шт.);
• — стеклу: 40/2 = 20 (шт.).

Оптимально возможен выпуск только 20 дверей ЛВС, что ограничивается наличием стекла. При этом уйдет 12 м [1] древесины, из оставшейся части возможен еще выпуск 40 шт. дверей ассортимента ДВ. На производство 20 шт. ДВС и 40 шт. ДВ будет потрачено 448 чел.-ч.

Прибыль составит 160 тыс. руб. (20 -2 + 40-3). Значит первая программа предпочтительней. Существуют и другие варианты.

Ограничения данной задачи таковы:

На графике проведем прямую L_u соответствующую первому неравенству: Второму неравенству соответствует прямая Ь₂:

Третьему неравенству на графике соответствует прямая, параллельная оси абсцисс L₃:

Поскольку план выпуска должен строиться исходя из всех пяти ограничений задачи, то областью допустимых решений в данном случае будет закрашенный многоугольник.

Максимальное значение целевой функции, найденное в предыдущих расчетах, будет соответствовать точкам прямой:

Многоугольник ограничивает область допустимых решений задачи. Из массы решений нужно выбрать такое, где значение прибыли максимально. В нашем случае эго будет точка пересечения прямых L и 1₂. Далее решается система линейных уравнений:

Решая систему, получаем: отсюда прибыль равна:

Если прямая, отвечающая целевой функции (в графическом методе) проходит через вершину многоугольника, то задача имеет единственный оптимальный вариант. Если совпадает со стороной многоугольника, то задача имеет множество решений.

Оптимальное решение должно проходить либо через вершину, либо через сторону многоугольника. Поэтому одна из вершин отвечает оптимальному решению, но неизвестно вначале какая.

Графический метод прост и нагляден, но применение его ограничено.

При трех переменных пришлось бы строить многогранник в многомерной системе координат. При четырех и более переменных графическое изображение невозможно. Но можно представить многомерное пространство абстрактно. Если условие задачи непротиворечиво, то область допустимых значений (ОДЗ) образует выпуклый многоугольник в и-мерном пространстве.

При этом оптимальное решение, если оно существует, обязательно достигается в некоторой вершине многогранника (возможно и более чем в одной).

Таким образом, чтобы найти решение задачи линейного программирования достаточно перебрать варианты, соответствующие вершинам многогранника. Они называются опорными планами. Однако в сложных задачах их может оказаться чрезмерно много и определение опорных планов потребует огромного объема вычислений.

Симплексный метод позволяет осуществить упорядоченный перебор вершин многогранника.

Последовательность расчетов по симплексному методу рассмотрим на примере.

Предприятие располагает тремя группами оборудования (I, II, III), па котором изготавливается четыре вида продукции (А, Б, В, Г). Все изделия имеют неограниченный сбыт и, следовательно, предприятие может планировать ассортиментную программу в пределах данной номенклатуры.

Имеются следующие ограничения:

• — наличие основного оборудования;
• — нормы времени на обработку каждого вида изделий на оборудовании каждой группы;
• — величина прибыли, полученная предприятием за единицу конкретного вида изделий.

Требуется получить максимальную прибыль.

Время на единицу изделия, мин

Месячный фонд времени, мин

Прибыль с единицы продукции, руб.

Максимальная прибыль:

Для решения задачи симплексным методом все неравенства превращаем в равенства. Для этого вводим в задачу три дополнительные неотрицательные переменные величины: х₅, х₆, х₇ и прибавляем их к левой части неравенства:

По своему экономическому смыслу дополнительные переменные есть ни что иное, как неиспользованное время работы конкретного оборудования. Для решения задач симплекс методом составляются специальные симплекс таблицы.

В самой верхней строке записаны коэффициенты целевой функции. Дополнительным переменным соответствуют нулевые коэффициенты. Неиспользованное оборудование не приносит прибыль. Те же нулевые показатели — в столбце С против каждой дополнительной переменной.

В заполнении строки Zj — Cj имеются свои особенности. Рассматривается Zj для каждого столбца. Она получается как сумма произведений величин столбца С на соответствующие коэффициенты столбца j. Поскольку в первоначальном варианте в столбце С находятся 0, то величина Zj для всех столбцов равна 0, а величина Zj — Cj = -Cj. Поэтому в начальном варианте здесь поставлены коэффициенты целевой функции с обратным знаком. Все основные переменные приравнены к 0 и не входят в базис нашей задачи. Дополнительные переменные равны предельным значениям в соответствии с исходными уравнениями. Это означает, что ничего не производится, ресурсы не используются и значение целевой функции равно 0 (прибыль отсутствует).

Решение задачи заключается в последовательном введении в план основных переменных, пока не будет получено оптимальное решение. При этом на каждом этапе расчета можно ввести лишь одну переменную. При этом другая переменная выводится из базы, так как при трех ограничениях в базисе не может быть больше трех переменных.

Поскольку задача решается на max прибыли, начинать надо с наиболее прибыльного изделия. В нашем случае это изд. Г. В базис вводится х₄. Определим, каким может быть предусмотрен выпуск изд. Г. Это зависит от объема ресурсов и нормативов затрат. На оборудовании группы I можно обработать 3000 изд. (24 000/8), группа II в изготовлении Г не участвует, а группа III может быть использована на обработку 30 000 изд. Принимаем наименьшее из значений (3000 изд.), в таблице в колонку «базис» х₄ ставится на место х₅ (оборудование группы I равняется нулю, так как использовано полностью). Число 8 на пересечении х_А и х₅ называется направляющим элементом или генеральным, ключевым, разрешающим.

Строка х₄ в новой таблице получается путем деления строки выводящей переменной х₅ предыдущей таблицы на направляющий элемент. В столбце С проставляется 0,8 — величина прибыли с единицы изд. Г. После этого пересчитывается столбец «план». На оборудовании группы II изд. Г не обрабатывается и в новом варианте фонд его времени остается без изменений (12 000 мин).

Фонд времени оборудования группы III уменьшится на 3000 мин (1 мин х х 3000 шт.), следовательно остаются неиспользованными 27 000 мин. Следующее число столбца «план» — 2400 руб. (0,8 • 3000) — прибыль при данном варианте. После столбца «план» пересчитываются все остальные столбцы симплексной таблицы, кроме строки вводимой переменной. При этом, следует иметь в виду, что в столбцах всех переменных, входящих в базис, на пересечении одноименных строк и столбцов всегда находится единица, а остальные элементы столбца равны нулю.

Поэтому сразу можно заполнить столбцы х₄, х₆ и х₇. Пересчет целесообразно производить по «правилу треугольника». Для того, чтобы рассчитать в новом варианте какой-либо коэффициент, нужно в симплексной таблице найти три числа: число, стоящее на месте этого коэффициента в предыдущем варианте;

• — число, стоящее в той же строке предыдущего варианта, но в столбце вводимой переменной;
• — число, находящееся в новом варианте в одном столбце с искомым коэффициентом, но в строке вновь введенной переменной (элементы этой строки ранее уже были рассчитаны).

Указанные три числа в таблице образуют прямоугольный треугольник. Для определения искомого коэффициента из числа, находящегося в вершине прямого угла необходимо вычесть произведение двух других углов.

для коэффициента по строке

для коэффициента строки х₇:

Показатель для строки Zj — Cj можно рассчитать двумя способами:

а) по формуле

б) по правилу «треугольника»:

Аналогично производим расчеты и для других столбцов нового варианта симплексной таблицы.

Теперь необходимо выяснить, является ли второй вариант оптимальным или он может быть улучшен. Для этого просматривается строка Zj — Cj. Если она содержит отрицательные числа, то вариант может быть улучшен.

На 0,3 руб. в расчете на каждую вводимую единицу изделий увеличится прибыль при введении в базис числах! (изд. А) и на 0,1 руб. при введении числах₃ (изд. В). Эти цифры могут показаться противоречащими исходным данным: согласно которым изд. А приносит 0,4 руб. прибыли, В — 0,5 руб. Но дело в том, что на данном этапе задачи введение в план этих изделий вытеснит известное количество ранее введенных изд. Г, чтобы для их производства высвободить оборудование группы I.

На следующем этане целесообразнее ввести х (изд. А), гак как ему соответствует наибольшее по абсолютной величине отрицательное число. Аналогично предыдущему варианту установим сколько едении изд. А может быть включено в план с учетом того, что он уже содержит выпуск изд. Г. Для этого числа из столбца «план» делим на соответствующие (только положительные) коэффициенты из столбца вводимой переменной х и из полученных частных выбираем наименьшее:

Отсюда следует, что в новый вариант расчета может быть введено не более 4000 изд. А, гак лимитирующим фактором является оборудование группы II. Следовательно, переменная х заменит в базисе переменную х_в.

На пересечении столбца х_х и строки х₆ находим и подчеркиваем направляющий элемент — 3. Далее рассчитываем строку введенной переменной путем деления элементов строки х₆ предыдущего варианта на направляющий элемент. Затем рассчитываем столбец «план»:

Прибыль при новом варианте составит:

По описанному правилу заполняем следующие столбцы. Просматривая строку Zj — Cj видим, что в ней содержатся только нули и положительные элементы, что означает, что вариант 3 является оптимальным решением и не может быть улучшен. В него входят лишь два вида изделий из четырех. Переменная х₃ соответствует в последней строке 0. Это означает, что введение в план на последующем шаге х₃ не увеличит прибыль, но и не уменьшит ее и полученный результат также будет оптимальным. Разделив числа столбца «план» на коэффициенты столбца х₃ и выбрав из полученных минимальное, определяем, что данная переменная должна вводиться в базис на место переменной^. В результате последующих преобразований получаем новый оптимальный план, в котором предусматривается выпуск 2182 изд. А (х₎ и 5455 изд. В (.г₃). Найдем еще несколько оптимальных вариантов решения нашей задачи. Вариант /: 50% из первой программы и 50% из второй программы:

Вариант II: 80% из первой программы и 20% из второй программы:

Эти варианты также обеспечивают прибыль в размере 3600 руб.

Наличие нескольких практически равных эффективных планов позволяет определить ряд промежуточных вариантов, что в экономических задачах дает дополнительные возможности для анализа и качественного отбора наиболее приемлемых из них.

При решении задач симплекс методом могут встретиться случаи «вырождения». При т ограничениях невырожденный план всегда содержит т положительных переменных, а остальные п — т переменных задачи в базис не входят и равняются нулю. Однако возможно равенство нулю и одной или нескольких переменных из входящих в базис, т.е. наличие одного или несколько нулей в столбце «план» симплексной таблицы. Такой план и называется вырожденным. При вырожденном плане наличие отрицательных чисел в строке Zj — Cj не означает, что следующий вариант обеспечит увеличение значения целевой функции. Оно может остаться неизмененным, причем на протяжении не только одного, но и нескольких последовательных шагов. Так происходит зацикливание, которое препятствует дальнейшим расчетам и может быть преодолено лишь с помощью специальных приемов.

В настоящее время при решении задач оптимизации широко применяются персональные компьютеры. При этом используется система электронных таблиц «Microsoft Excel».

Для решения задач оптимизации в MS Excel используют надстройку Поиск решения, которая вызывается из пункта главного меню «Сервис».

Если в версии Excel, установленной на вашем компьютере, отсутствует данный подпункт меню «Сервис», необходимо вызвать пункт меню «Надстройки» и в предложенном списке дополнительных модулей выбрать «Поиск решения».

Рассмотрим на примере использование данной надстройки, решив с ее помощью задачу производственного планирования.

Предприятие выпускает продукты А, В, С, D из трех типов ресурсов. Математическая модель имеет следующий вид: шах/(Х) = 7,5я*₁+3х₂ + 6дг₃ + 12.г₄ (целевая функция — суммарная стоимость выпуска).

Ограничения по запасам ресурсов и неотрицательности переменных таковы:

Составим шаблон в редакторе Excel.

Теперь занесем в данную задачу числовую информацию.

В выделенные пустые ячейки (значения целевой функции и левых частей неравенств) необходимо занести формулы, отображающие связи и отношения между числами на рабочем столе.

Ячейки С₄ — F_a называются в Excel изменяемыми (в нашей модели это неизвестные переменные). Поиск решения при их изменении будет находить оптимальное значение целевой функции. Значения, которые первоначально вводят в эти ячейки, обычно нули (незаполненные клетки трактуются по умолчанию как содержащие нулевые значения).

Теперь необходимо ввести формулы. В нашей математической модели целевая функция представляет собой произведение вектора коэффициентов на вектор неизвестных. Действительно, выражение можно рассматривать

как произведение вектора (7, 5, 3, б, 12) на вектор (.г,, х₂, я-*, х_А).

В Excel существует функция СУММПРОИЗВ, которая позволяет найти скалярное произведение векторов. Данную функцию необходимо вызвать в ячейку #5, а в качестве перемножаемых векторов задать адреса ячеек, содержащих коэффициенты уравнений (в данном случае, это С5 : F5), и ячеек, в которые в результате решения будут помещены значения х_и х₂, х₃, х₄ (ячейки СА : FA).

Каждая левая часть ограничения тоже представляет собой произведение двух векторов: соответствующей строки матрицы затрат и вектора неизвестных. Выражение 2х_х + х₂ + 0Дг₃ + 4х_л (для первого ограничения 2х, + х₂ + 0,5х₃ + 4 х₄

источник

При решении конкретной задачи оптимизации исследователь прежде всего должен выбрать математический метод, который приводил бы к конечным результатам с наименьшими затратами на вычисления или же давал возможность получить наибольший объем информации об искомом решении. Выбор того или иного метода в значительной степени определяется постановкой опти­мальной задачи, а также используемой математической моделью объекта оптимизации.

В настоящее время для решения оптимальных задач применяют в основном следующие методы:

1. Методы исследования функций классического анализа.

Методы, основанные на использовании неопределенных множителей Лагранжа.

2. Методы исследования функций численного анализа.

2. 1. Линейное программирование.

2.3. Нелинейное программирование.

2.4. Динамическое программирование.

В последнее время разработан и успешно применяется для реше­ния определенного класса задач также метод геометрического программи­рования.

Как правило, нельзя рекомендовать какой-либо один метод, ко­торый можно использовать для решения всех без исключения за­дач, возникающих на практике. Одни методы в этом отношении являются более общими, другие — менее общими. Наконец, целую группу методов (методы исследования функций классического анализа, метод множителей Лагранжа, методы нелинейного программирования) на определенных этапах решения оптимальной задачи можно применять в сочетании с другими методами, например динамическим программированием или принципом максимума. Отметим также, что некоторые методы специально разработаны или наилучшим образом подходят для решения оптимальных задач с математическими моделями определенного вида. Так, математический аппарат линейного программирования специально создан для решения задач с линейными критериями оптимальности и линейными ограничениями на переменные и позволяет решать большинство задач, сформулированных в такой постановке. Геометрическое программирование предназначено для решения оптимальных задач, в которых критерий оптимальности и ограничения представляются специального вида функциями — позиномов. Динамическое программирование хорошо приспособлено для решения задач оптимизации многостадийных процессов, особенно тех, в которых состояние каждой стадии характеризуется относительно небольшим числом переменных состояния. Однако при наличии значительного числа этих переменных, т. е. при высокой размерности каждой стадии, применение метода динамической программирования затруднительно вследствие ограниченных быстродействия и объема памяти вычислительных машин

Методы исследования функций классического анализа

Методы исследования функций классического анализа представляют собой наиболее известные методы решения несложных оптимальных задач. Обычной областью использования данных методов являются задачи с известным аналитическим выражением критерия оптимальности, что позволяет найти не очень сложное, также аналитическое выражение для производных. Полученные приравниванием нулю производных уравнения, определяющие экстремальные решения оптимальной задачи крайне редко удается решить аналитическим путем, поэтому, как правило, применяют вычислительные машины. Дополнительные трудности при решении оптимальной задачи методами исследования функций классического анализа возникают вследствие того, что система уравнений, получаемая в результате их применения, обеспечивает лишь необходимые условия оптимальности. Поэтому все решения данной системы (а их может быть и несколько) должны быть проверены на достаточность. В результате такой проверки сначала отбрасывают решения, которые не определяют экстремальные значения критерия оптимальности, а затем среди остающихся экстремальных решений выбирают решение, удовлетворяющее условиям оптимальной задачи, т. е. наибольшему или наименьшему значению критерия оптимальности в зависимости от постановки задачи. Методы исследования при наличии ограничений на область изменения независимых переменных можно использовать только для отыскания экстремальных значений внутри указанной области. В особенности это относится к задачам с большим числом независимых переменных (практически больше двух), в которых анализ значений критерия оптимальности на границе допустимой области изменения переменных становится весьма сложным. Метод множителей Лагранжа применяют для решения задач такого же класса сложности, как и при использовании обычных методов исследования функций, но при наличии ограничений типа равенств на независимые переменные. К требованию возможности получения аналитических выражений для производных от критерия оптимальности при этом добавляется аналогичное требование относительно аналитического вида уравнений ограничений. В основном при использовании метода множителей Лагранжа приходится решать те же задачи, что и без ограничений. Некоторое усложнение в данном случае возникает лишь от введения дополнительных неопределенных множителей, вследствие чего порядок системы уравнений, решаемой для нахождения экстремумов критерия оптимальности, соответственно повышается на число ограничений. В остальном процедура поиска решений и проверки их на оптимальность отвечает процедуре решения задач без ограничений. Множители Лагранжа можно применять для решения задач оптимизации объектов с распределенными параметрами и задач динамической оптимизации. При этом вместо решения системы конечных уравнений для отыскания оптимума необходимо интегрировать систему дифференциальных ураавнений. Следует отметить, что множители Лагранжа используют также в качестве вспомогательного средства и при решении специальными методами задач других классов с ограничениями типа равенств, например, в вариационном исчислении и динамическом программировании. Особенно эффективно применение множителей Лагранжа в методе динамического программирования, где с их помощью иногда удается снизить размерность решаемой задачи. Методы вариационного исчисления обычно ис­пользуют для решения задач, в которых критерии оптимальности представляются в виде функционалов и решениями которых служат неизвестные функции. Такие задачи возникают обычно при статической оптимизации процессов с распределенными парамет­рами или в задачах динамической оптимизации. Вариационные методы позволяют в этом случае свести решение оптимальной задачи к интегрированию системы дифференциальных уравнений Эйлера, каждое из которых является нелинейным диф­ференциальным уравнением второго порядка с граничными усло­виями, заданными на обоих концах интервала интегрирования. Число уравнений указанной системы при этом равно числу неиз­вестных функций, определяемых при решении оптимальной задачи. Каждую функцию находят в результате интегрирования получае­мой системы. Уравнения Эйлера выводятся как необходимые условия экс­тремума функционала. Поэтому полученные интегрированием си­стемы дифференциальных уравнений функции должны быть про­верены на экстремум функционала. При наличии ограничений типа равенств, имеющих вид функ­ционалов, применяют множители Лагранжа, что дает возможность перейти от условной задачи к безусловной. Наиболее значитель­ные трудности при использовании вариационных методов возни­кают в случае решения задач с ограничениями типа неравенств. Заслуживают внимания прямые методы решения задач опти­мизации функционалов, обычно позволяю­щие свести исходную вариационную задачу к задаче нелиней­ного программирования, решить которую иногда проще, чем крае­вую задачу для уравнений

Методы исследования функций численного анализа.

Линейное программирование представляет собой математический аппарат, разработанный для решения оптимальных задач с линейными выражениями для критерия оптимальности и линейными ограничениями на область изменения переменных. Такие задачи обычно встречаются при решении во­просов оптимального планирования производства с ограниченным количеством ресурсов, при определении оптимального плана пе­ревозок (транспортные задачи) и т. д. Для решения большого круга задач линейного программирова­ния имеется практически универсальный алгоритм — симплексный метод, позволяющий за конечное число итераций находить опти­мальное решение подавляющего большинства задач. Тип исполь­зуемых ограничений (равенства или неравенства) не сказывается на возможности применения указанного алгоритма. Дополнитель­ной проверки на оптимальность для получаемых решений не тре­буется. Как правило, практические задачи линейного программиро­вания отличаются весьма значительным числом независимых пере­менных. Поэтому для их решения обычно используют вычислитель­ные машины, необходимая мощность которых определяется раз­мерностью решаемой задачи.

Принцип максимума применяют для решения задач оптимизации процессов, описываемых системами дифферен­циальных уравнений. Достоинством математического аппарата принципа максимума является то, что решение может определяться в виде разрывных функций; это свойственно многим задачам оптимизации, например задачам оптимального управления объек­тами, описываемыми линейными дифференциальными уравне­ниями Нахождение оптимального решения при использовании принципа максимума сводится к задаче интегрирования системы диф­ференциальных уравнений процесса и сопряженной системы для вспомогательных функций при граничных условиях, заданных на обоих концах интервала интегрирования, т. е. к решению краевой задачи. На область изменения переменных могут быть наложены ограничения. Систему дифференциальных уравнений интегрируют применяя обычные программы на цифровых вычислительных машинах. Принцип максимума для процессов, описываемых дифферен­циальными уравнениями, при некоторых предположениях является и достаточным условием оптимальности. Поэтому дополнительной проверки на оптимум получаемых решений обычно не требуется. Для дискретных процессов принцип максимума в той же фор­мулировке, что и для непрерывных, вообще говоря, несправедлив. Однако условия оптимальности, получаемые при его применении для многостадийных процессов, позволяют найти достаточно удобные алгоритмы оптимизации

Методы нелинейного программирования приме­няют для решения оптимальных задач с нелинейными функциями цели. На независимые переменные могут быть наложены ограни­чения также в виде нелинейных соотношений, имеющих вид ра­венств или неравенств. По существу методы нелинейного програм­мирования используют, если ни один из перечисленных выше ме­тодов не позволяет сколько-нибудь продвинуться в решении оптимальной задачи. Поэтому указанные методы иногда называют также прямыми методами решения оптимальных задач. Для получения численных результатов важное место отводится нелинейному программированию и в решении оптимальных задач такими методами, как динамическое программирование, принцип, максимума и т. п. на определенных этапах их применения. Названием «методы нелинейного программирования» объеди­няется большая группа численных методов, многие из которых при­способлены для решения оптимальных задач соответствующего класса. Выбор того или иного метода обусловлен сложностью вы­числения критерия оптимальности и сложностью ограничивающих условий, необходимой точностью решения, мощностью имеющейся вычислительной машины и т. д. Ряд методов нелинейного програм­мирования практически постоянно используется в сочетании с дру­гими методами оптимизации, как, например, метод сканирования в динамическом программировании. Кро­ме того, эти методы служат основой построения систем автомати­ческой оптимизации — оптимизаторов, непосредственно при­меняющихся для управления производственными процессами.

Динамическое программирование служит эффек­тивным методом решения задач оптимизации дискретных многоста­дийных процессов, для которых критерий оптимальности задается как аддитивная функция критериев оптимальности отдельных ста­дий. Без особых затруднений указанный метод можно распростра­нить и на случай, когда критерий оптимальности задан в другой форме, однако при этом обычно увеличивается размерность отдель­ных стадий. По существу метод динамического программирования представ­ляет собой алгоритм определения оптимальной стратегии управле­ния на всех стадиях процесса. При этом закон управления на ка­ждой стадии находят путем решения частных задач оптимизации последовательно для всех стадий процесса с помощью методов ис­следования функций классического анализа или методов нелиней­ного программирования. Результаты решения обычно не могут быть выражены в аналитической форме, а получаются в виде таб­лиц. Ограничения на переменные задачи не оказывают влияния на общий алгоритм решения, а учитываются при решении частных за­дач оптимизации на каждой стадии процесса. При наличии ограни­чений типа равенств иногда даже удается снизить размерность этих частных задач за счет использования множителей Лагранжа.

Применение метода динамического программирования для оп­тимизации процессов с распределенными параметрами или в зада­чах динамической оптимизации приводит к решению дифферен­циальных уравнений в частных производных. Вместо решения таких уравнений зачастую значительно проще представить непре­рывный процесс как дискретный с достаточно большим числом стадий. Подобный прием оправдан особенно в тех случаях, когда имеются ограничения на переменные задачи и прямое решение дифференциальных уравнений осложняется необходимостью учета указанных ограничений. При решении задач методом динамического программирования, как правило, используют цифровые вычислительные машины обла­дающие достаточным объемом памяти для хранения промежуточ­ных результатов решения, которые обычно получаются в таблич­ной форме.

Геометрическое программирование — есть метод решения одного специального класса задач нелинейного программирования, в которых критерий оптимальности и ограничены задаются в виде позиномов — выражений, представляющих собой сумму произведений степенных функций от независимых перемен­ных. С подобными задачами иногда приходится сталкиваться в проектировании. Кроме того, некоторые задачи нелинейного про­граммирования иногда можно свести к указанному представлению, используя аппроксимационное представление для целевых функций и ограничений.

Решение оптимальной задачи, полученное с использованием математической модели процесса, всегда дает лишь идеализированное представление об оптимальном режиме реального процесса, так как никакая модель не может полностью заменить оптимизируемый объект. Кроме того, при применении такого режима неизбежны отклонения от найденного закона оптимального управления. Поэтому, прежде чем перейти к вопросам практической реализации оптимального режима, интересно хотя бы приближенно оценить чувствительность найденного оптимального решения к изменению параметров, модели в частности, к изменению управляющих действий. Под чувствительностью оптимума ниже будет пониматься относительное изменение критерия оптимальности при отклонении управляющих воздействий от оптимальных значений.Вообще говоря, в приведенное определение чувствительности оптимума следует включить не только зависимость критерия от управляющих воздействий, но также и от всех остальных параметров математической модели, для которых в процессе моделирования необходимо задавать численные значения. В этом случае постановка задачи исследования чувствительности оптимума найденного на математической модели процесса, окажется наиболее полной. Однако принципиально анализ чувствительности оптимума несмотря на то, по какому параметру ее исследуют, проводят аналогичным методами. Поэтому в дальнейшем ограничимся рассмотрением чувствительности только по отношению к управляющим воздействиям. Предположим, что известно оптимальное управление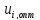(i= 1, . . . ,r), максимизирующее значение критерия оптимальностиR, который при этом принимается только как функция управляющих воздействий:

R=R(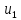,…,) (1,33)

При отклонении управляющих воздействий от оптимальных знаний 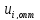на величиныизменение критерия оптимальности определяется выражением:

?R=R(,…,+?)-R(,…,) (1,34)

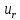
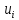
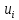
Для малых значений ?оценка изменения критерия оптимальности может быть получена разложением правой части выражения (I,34) в ряде по степеням?с точностью до членов второго порядка малости:

?R=+ (1,35)

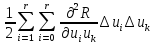
Полагая, что оптимум находится внутри допустимой области изменения значений управляющих воздействий и что функция R по крайней мере дважды дифференцируема в этой области, для опти­мального управления будем иметь:

=0 i = 1,…,r (1,36)

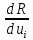
С учетом равенства (1,36) выражение для оценки изменения критерия оптимальности можно записать в виде:

(1,37)

Допустим, что максимальное отклонение управляющих воздей­ствий от оптимального значения не превышает величины 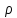. В дан­ном случае может быть принято неравенств

I,k=1,…,r(1, 38)

Комбинируя выражения (1,37) и (1,38), получим следующую оценку для изменения критерия оптимальности:

,

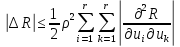
где производные суммируют по модулю для того, чтобы учесть воз­можное различие их знаков. Для оценки размеров окрестности _м, в которой допустимо из­менение значений управляющих воздействий при изменении крите­рия оптимальности не более чем на из выражения (1,39) получим формулу

, (1,40)

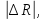
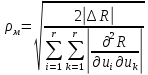
которая для одного управляющего воздействия имеет простой вид:

(1,41)

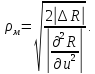
Специфической особенностью методов решения оптимальных задач (за исключением методов нелинейного программирования) является то, что до некоторого этапа оптимальную задачу решают аналитически, т. е. находят определенные аналитические выраже­ния, например, системы конечных или дифференциальных уравне­ний, откуда уже отыскивают оптимальное решение. В отличие от указанных методов при использовании методов нелинейного про­граммирования, которые, как уже отмечалось выше, могут быть названы прямыми, применяют информацию, получаемую при вы­числении критерия оптимальности, изменение которого служит оценкой эффективности того или иного действия. Важной характеристикой любой оптимальной задачи является ее размерность п, равная числу переменных, задание значений ко­торых необходимо для однозначного определения состояния опти­мизируемого объекта. Как правило, решение задач высокой раз­мерности связано с необходимостью выполнения большого объема вычислений. Ряд методов (например, динамическое программиро­вание и дискретный принцип максимума) специально предназначен для решения задач оптимизации процессов высокой размерно­сти, которые могут быть представлены как многостадийные про­цессы с относительно невысокой размерностью каждой стадии.

В табл. 1 дана характеристика областей применения различ­ных методов оптимизации, при этом за основу положена сравни­тельная оценка эффективности использования каждого метода для решения различных типов оптимальных задач. Классификация за­дач проведена по следующим признакам:

1) Вид математического описания процесса;

2) Тип ограничений на переменные процесса;

Предполагается, что решение оптимальной задачи для процессов, описываемых системами конечных уравне­ний, определяется как конечный набор значений управляющих воз­действий (статическая оптимизация процессов с сосредоточенными параметрами), а для процессов, описываемых системами обыкно­венных дифференциальных уравнений, управляющие воздействия характеризуются функциями времени (динамическая оптимизация процессов с сосредоточенными параметрами) или пространствен­ных переменных (статическая оптимизация процессов с распрелеленными параметрами Классификация задач по группам с числом независимых пере­менных, большим и меньшим трех или равным трем как характе­ристика размерности задач с большим и малым числом перемен­ных, разумеется, весьма условна и в данном случае выбрана скорее, из соображений наглядности графического изображения пространства изменения переменных задачи — фазового простран­ства (при числе переменных большем трех графическое изображе­ние фазового пространства обычными приемами отсутствует) Тем не менее, такая классификация до некоторой степени все же отражает действительные трудности, возникающие при решении задач с размерностью выше трех.Пространства изменения переменных задачи – фазового пространства (при числе переменных большем трех графическое изображение фазового пространства обычными приемами отсутствует). Тем не менее, такая классификация до некоторой степени все же отражает действительные трудности, возникающие при решении задач с размерностью выше трех.

Таблица «Области применения методов оптимизации»

1. Эффективное применение метода.

4. Используется как вспомогатель­ный метод.

5. Многостадийные процессы (размерность указывается для отдельной стадии).

6. Задачи с линейными критериями оптималь­ности и линейными ограничениями.

7. Используются множители Лагранжа.

8. Задачи с критериями и ограничениями в форме позиномов.

источник

Бюджетное профессиональное образовательное учреждение

Омской области «Сибирский профессиональный колледж»

МАТЕМАТИЧЕСКИЕ МЕТОДЫ. Линейное программирование.

Для студентов очной формы обучения специальности

Программирование в компьютерных системах»

ОБЩАЯ ПОСТАНОВКА ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ.. 4

Практическая работа № 1. «Построение математической модели задачи линейного программирования» 9

Практическая работа №2. «Графическое решение задачи линейного программирования». 12

Практическая работа №3. «Симплексный метод решения задачи линейного программирования» 18

Практическая работа № 4. « Симплексные таблицы». 22

Практическая работа № 5. « Расчет задач линейного программирования с использованием MS Excel» 26

Практическая работа № 6.1. « Транспортная задача. Метод Северо-западного угла». 31

Практическая работа №6.2. «Транспортная задача. Метод наименьших затрат». 35

Практическая работа № 7. «Транспортная задача. Открытая модель». 37

Практическая работа № 8.1. «Транспортная задача. Проверка оптимальности решения. Метод потенциалов». 40

Практическая работа № 8.2. « Транспортная задача с ограничениями». 45

Практическая работа № 8.3. «Решение транспортной задачи с помощью MS Excel». 48

Практическая работа № 9. «Задача о назначениях». 51

Практическая работа № 10. «Решение задачи о назначениях с помощью MS Excel». 55

Индивидуальная контрольная работа.. 57

БИБЛИОГРАФИЧЕСКИЙ СПИСОК.. 63

ПОЯСНИТЕЛЬНАЯ ЗАПИСКА

Настоящее учебное пособие разработано для студентов очной формы обучения специальности 230115 «Программирование в компьютерных системах» при изучении дисциплины «Математические методы».

В учебном пособии кратко изложен теоретический материал, адаптированный для практических целей и пояснения к решению задачи линейного программирования математическими методами, которые необходимо применить при выполнении практических работ и индивидуальной контрольной работы в соответствии с индивидуальным вариантом контрольного задания студента.

ОБЩАЯ ПОСТАНОВКА ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ

Линейное программирование. Сущность линейного программирования

Линейное программирование относится к числу наиболее широко распространенных методов исследования операций, используемых при решении производственных и коммерческих задач.

Исследование операций– это наука, занимающаяся разработкой и практическим применением методов наиболее эффективного (оптимального) управления организационными системами.

Целью исследования операций является количественное обоснование принимаемых решений для выявления лучшего (оптимального) способа действий при решении той или иной задачи организационного управления.

Основной задачей исследования операций является предварительное количественное обоснование оптимальных решений.

При решении конкретной задачи управления применение методов исследования операций предполагает:

1. Построение экономико-математических моделей для задач принятия решения в сложных ситуациях или в условиях неопределенности;

2. Изучение взаимосвязей, определяющих впоследствии принятие решений, и установление критериев эффективности, позволяющих оценивать преимущество того или иного варианта действия.

Основные этапы исследования операций:

2. Построение экономико-математической модели;

3. Определение метода решения задачи;

5. Проверка и корректировка математической модели;

6. Реализация найденного решения на практике.

Примерами задач исследования операций, отражающих его специфику, могут служить следующие задачи.

Задача 1. Для обеспечения высокого качества выпускаемых изделий на заводе организуется система выборочного контроля. Требуется выбрать такие формы его организации — например, назначить размеры контрольных партий, указать последовательность контрольных операций, определить правила отбраковки, — чтобы обеспечить необходимое качество при минимальных расходах.

Задача 2.Для реализации определенной партии сезонных товаров создается сеть временных торговых точек. Требуется выбрать параметры сети — число точек, их размещение, количество персонала — так, чтобы обеспечить максимальную экономическую эффективность распродажи.

Задача 3. К заданному сроку необходимо провести массовое медицинское обследование группы населения с целью выявления определенных заболеваний. На обследование выделены материальные средства, оборудование, персонал. Требуется разработать такой план обследования — установить число медпунктов, их размещение, вид и количество анализов, чтобы выявить как можно больший процент из числа заболевших.

Необходимо отметить также задачи об использовании ресурсов (планирования производства), о смесях, об использовании мощностей (загрузке оборудования), о раскрое материалов, транспортную задачу и др., в которых требуется найти решение, когда некоторый критерий эффективности (например, прибыль, выручка, затраты ресурсов и т.п.) принимает максимальное или минимальное значение.

Приведенные задачи относятся к разным областям практики, но в них есть общие черты: в каждом случае речь идет о каком-то управляемом мероприятии (операции), преследующем определенную цель. В задаче 1 — это организация выборочного контроля с целью обеспечить качество выпускаемой продукции; в задаче 2 — организация временных торговых точек с целью проведения сезонной распродажи; в задаче 3 — массовое медицинское обследование с целью определения процента заболевших. В каждой задаче заданы некоторые условия проведения этого мероприятия, в рамках которых следует принять решение — такое, чтобы мероприятие принесло определенную выгоду. Условиями проведения операции в каждой задаче оказываются средства, которыми мы располагаем, время, оборудование, технологии, а решение в задаче 1 заключается в выборе формы контроля — размера контрольных партий, правил отбраковки; в задаче 2 — в выборе числа точек размещения, количества персонала; в задаче 3 — в выборе числа медпунктов, вида и количества анализов.

Рассмотрим краткое содержание каждого этапа исследования операций.

Постановка задачи – это чрезвычайно ответственный этап операционного исследования.

Первоначально задачу формулируют с точки зрения заказчика. Такая постановка задачи обычно не бывает окончательной. Во время анализа исследуемой системы задача постепенно уточняется.

2 этап. Построение экономико-математической модели.

Получив достаточно строгую и логически непротиворечивую, содержательную постановку задачи, нужно построить ее математическую модель. Этот процесс называется формализацией задачи.

При построении модели операция, как правило, упрощается, схематизируется и схема операции описывается с помощью того или иного математического аппарата. Модель операции — это достаточно точное описание операции с помощью математического аппарата (различного рода функций, уравнений, систем уравнений и неравенств и т.п.). Составление модели операции требует понимания сущности описываемого явления и знания математического аппарата.

Математическая модель должна отражать важнейшие черты явления, все существенные факторы, от которых в основном зависит успех операции. Вместе с тем, модель должна быть по возможности простой, не «засоренной» массой мелких второстепенных факторов: их учет усложняет математический анализ и делает труднообозримыми результаты исследования.

Эффективность операции — степень ее приспособленности к выполнению задачи — количественно выражается в виде критерия эффективности — целевой функции.

Например, в задаче об использовании ресурсов критерий эффективности — прибыль от реализации произведенной продукции, которую нужно максимизировать, в транспортной задаче — суммарные затраты на перевозку грузов от поставщиков к потребителям, которые нужно минимизировать. Выбор критерия эффективности определяет практическую ценность исследования. (Неправильно выбранный критерий может принести вред, ибо операции, организованные под углом зрения такого критерия эффективности, приводят порой к неоправданным затратам.)

Все факторы, входящие в описание операции, можно разделить на две группы:

1. Постоянные факторы (условия проведения операции), на которые мы влиять не можем. Обозначим их через α₁,α₂,……;

2. Зависимые факторы (элементы решения) x1,x2,…. которые в известных пределах мы можем выбирать по своему усмотрению.

Например, в задаче об использовании ресурсов к постоянным факторам следует отнести запасы ресурсов каждого вида, производственную матрицу, элементы которой определяют расход сырья каждого вида на единицу выпускаемой продукции каждого вида. Элементы решения — план выпуска продукции каждого вида.

Критерий эффективности, выражаемый некоторой функцией, называемой целевой, зависит от факторов обеих групп, поэтому целевую функцию Z можно записать в виде

Следует отметить, прежде всего, большой класс оптимизационных моделей. Такие задачи возникают при попытке оптимизировать планирование и управление сложными системами, в первую очередь экономическими системами. Оптимизационную задачу можно сформулировать в общем виде: найти переменные x₁, ,x₂,…. x_n, удовлетворяющие системе неравенств (уравнений):

(1)

и обращающие в максимум(или минимум) целевую функцию, т.е.

(2)

(Условия неотрицательности переменных, если они есть, входят в ограничения (1))

Как известно, упорядоченная совокупность значений n переменных x₁, x₂,….. x_n представляется точкой n-мерного пространства. В дальнейшем эту точку будем обозначать Х= (x₁, x₂,….. x_n), а само оптимальное решение Х*= (x₁*, x₂*,….. x_n*).

Таким образом, математическая модель задачи линейного программирования (ЗЛП) составляется путем экономического анализа по следующей схеме:

2. Формируют целевую функцию;

4. Налагают условия неотрицательности переменных (или указывают интервалы изменения переменных).

3 этап. Определение метода решения задач.

Для нахождения оптимального решения Х* в зависимости от структуры математической модели и существующих ограничений применяются следующие методы математического программирования:

1. Линейноепрограммирование применяют в том случае, когда функции ¦и φ являются линейными функциями относительно переменных;

2. Нелинейное программирование, если ¦ и φ – нелинейные функции;

3. Динамическоепрограммирование применяется в том случае, когда ¦ и φ имеет специфическую структуру и их поведение на каждом этапе зависит от всех предыдущих состояний;

4. Стохастическоепрограммирование применяют в том случае, когда переменные x и y являются случайными величинами;

5. Дискретноепрограммирование применяется в том случае, если на переменные x и y наложено условие дискретности (они могут принимать значение только 0 и 1);

6. Эвристическоепрограммирование применяют для решения задач, у которых точное оптимальное решение невозможно найти алгоритмическим путем. Выбор решения осуществляют практики-профессионалы с помощью специальных методик, называемых эвристиками.

В зависимости от сложности и объема исходной информации, решение задачи может выполняться либо с помощью ручного счета с использованием калькулятора, либо с привлечением специально разработанных программ.

5 этап. Проверка и корректировка математической модели.

В сложных системах математическая модель лишь частично отражает реальный процесс, поэтому необходима проверка соответствия или адекватности математической модели и реального процесса. Корректировка может потребовать дополнительных исследований объекта, уточнения построения математической модели и изменения переменных. Таким образом, четыре предыдущих этапа, могут повторяться до тех пор, пока не будет достигнуто удовлетворительное соответствие выходных характеристик математической модели и реального процесса.

6 этап. Реализация решения на практике.

Полученное математическое решение облекают в документальную форму, снабжают многими подробными инструкциями и рекомендациями по решению и передают заказчику в виде технического проекта.

Замечание. Следует обратить внимание на постановку проблемы: само принятие решений выходит за рамки исследования операций и относится к компетенции ответственного лица или группы лиц, которые могут учитывать и другие соображения, отличные от математически обоснованных.

Задачи линейного программирования являются самыми простыми среди задач математического программирования. Они являются широко используемыми методами решения экономических и производственных задач. Для задач линейного программирования характерно то, что:

– показатель эффективности (целевая функция) зависит линейно от элементов решения x₁, x₂. ,x_n;

– ограничения, наложенные на элементы решения, имеют вид линейных равенств или неравенств относительно x₁, x₂. ,x_n.

Такие задачи довольно часто встречаются на практике, например, при решении проблем, связанных с распределением ресурсов, планирования производства, организацией работы транспорта и т. д. Это естественно, т. к. во многих задачах практики «расходы» и «доходы» линейно зависят от количества закупаемых средств.

В линейном программировании используются две основные аксиомы:

1. Аддитивности, т.е. полное количество ресурсов, затрачиваемых на производство единицы продукции равно сумме всех ресурсов;

2. Пропорциональности, т.е. все показатели, используемые в уравнениях математической модели, могут быть увеличены или уменьшены в любое число раз. При этом сохраняется их взаимная пропорциональность.

Любую задачу линейного программирования можно свести к стандартной форме, так называемой «основой задачей линейного программирования», которая формулируется так:

Дана система m линейных уравнений и неравенств с n переменными

(3)

и линейная функция .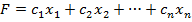

Необходимо найти такое решение системы , где

при котором линейная функция Fпринимает оптимальное (то есть максимальное или минимальное) значение.

Система (3) называется системой ограничений, а функция F – линейной функцией, линейной формой, целевой функцией или функцией цели.

Всякий определенный выбор зависящих от нас параметров называется решением.Оптимальнымназывается решение, которое по тем или иным признакам предпочтительнее перед другими решениями.

Операция – система действий, объединенная единым замыслом и направленная к достижению поставленной цели.

По содержательной постановке можно выделить следующие типичные классы задач:

1. Задачи управления запасами.

2. Задачи распределения ресурсов.

3. Задачи ремонта и замены оборудования.

4. Задачи массового обслуживания.

6. Задачи сетевого планирования и управления.

7. Задачи выбора маршрута и другие.

Методы исследования операций, как и любые математические методы, всегда в той или иной мере упрощают, огрубляют задачу, отражая порой нелинейные процессы линейными моделями, стохастические системы — детерминированными, динамические процессы — статическими моделями и т.д. Жизнь богаче любой схемы.

Практические работы

Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: При сдаче лабораторной работы, студент делает вид, что все знает; преподаватель делает вид, что верит ему. 9454 — | 7325 — или читать все.

193.124.117.139 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.

Отключите adBlock!
и обновите страницу (F5)
очень нужно

источник