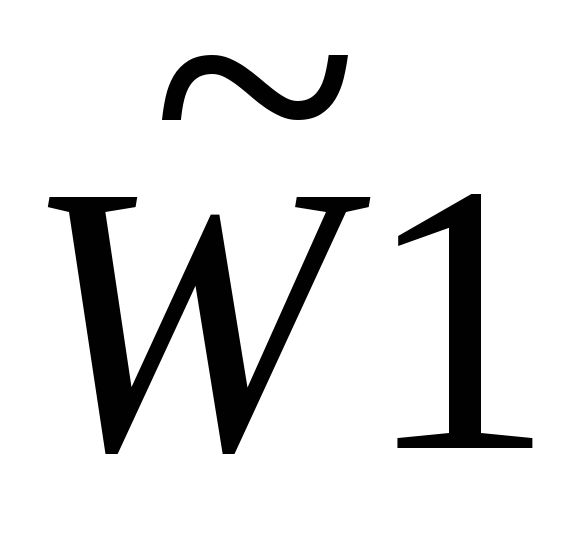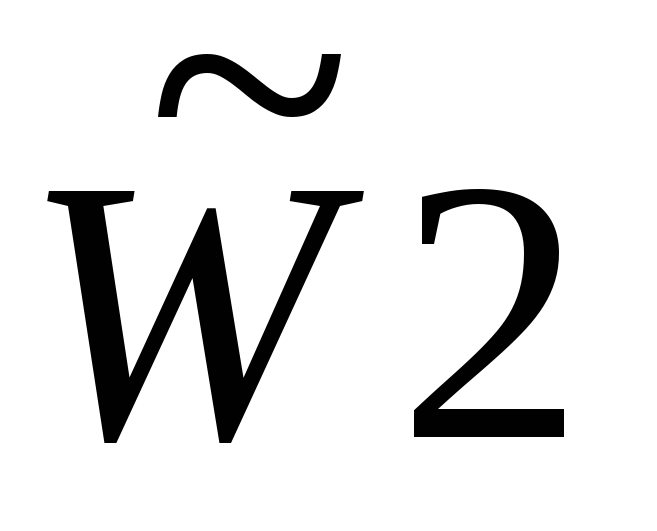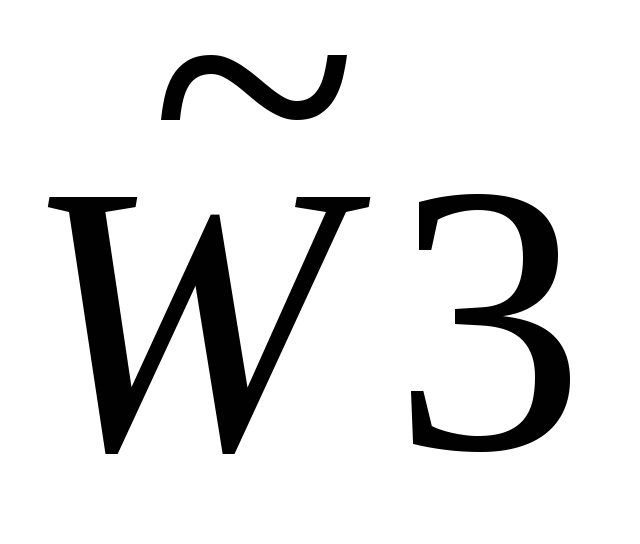1. Очертить проблему и определить, что мы хотим
2. Построить иерархию ( цель, критерии, альтернативы)
3. Построить множество матриц парных сравнений для каждого из нижних уровней по одной матрице для каждого элемента примыкающего сверху уровня
4. Проверить индекс согласованности каждой матрицы
5. Использовать иерархический синтез для взвешивания собственных векторов
Основные определения и понятия
Иерархия есть определенный тип системы, основанный на предположении, что элементы системы могут группироваться в несвязанные множества. Элементы каждой группы находятся под влиянием элементов некоторой вполне определенной группы и, в свою очередь, оказывают влияние на элементы другой группы. Мы считаем, что элементы в каждой группе иерархии (называемой уровнем, кластером, стратой) независимы.
Основной задачей в иерархии является оценка высших уровней исходя из взаимодействия различных уровней иерархии, а не из непосредственной зависимости от элементов на этих уровнях.
Точные методы построения систем в виде иерархий постепенно появляются в естественных и общественных науках, и особенно в задачах общей теории систем, связанных с планированием и построением социальных систем. Концептуально, наиболее простая иерархия — линейная, восходящая от одного уровня элементов к соседнему уровню. Например, в процессе производства имеется уровень рабочих, доминируемый уровнем мастеров, который в свою очередь доминируется уровнем управляющих и т. д., до вице-президентов и президента. В нелинейной иерархии верхний уровень может быть как в доминирующем положении по отношению к нижнему уровню, так и в доминируемом (например, в случае потока информации).
Естественные системы, составленные иерархически, т. е. посредством модульного построения и затем сборки модулей, строятся намного эффективнее, чем системы, собранные в целом.
Иерархии устойчивы и гибки; они устойчивы в том смысле, что малые изменения вызывают малый эффект, а гибкие в том смысле, что добавления к хорошо структурированной иерархии не разрушают ее характеристик.
Преимуществом метода анализа иерархий над большинством существующих методов оценивания альтернатив является чёткое выражение суждений экспертов и ЛПР, а также ясное представление структуры проблемы: составных элементов проблемы и взаимосвязей между ними.
Иерархия строится следующим образом: сначала определяется цель принятия решения (фокус проблемы). Это высший уровень иерархии. Например, выбор наилучшего места работы, ВУЗа для учёбы и т.д. За фокусом следует уровень наиболее важных критериев (оплата труда, время, необходимое для проезда на работу, и т.д.). Каждый критерий может делиться на субкритерии. За субкритериями следует уровень альтернатив, число которых может быть достаточно большим. Декомпозиция проблемы в иерархию зависит от хода мысли ЛПР, его концепции решения проблемы, интуиции и опыта.
Рассмотрим упрощённую модель принятия решения о выборе места работы. Есть три места работы: А1, А2 и А3
При выборе работы учитываются четыре критерия: зарплата, удалённость от дома, перспективы карьерного роста и риск потери работы.
Полученная иерархия соответствует 3-уровневой полной иерархии с фокусом принятие решения. Иерархия называется полной, если между элементами соседних уровней имеются все возможные связи.
Рассмотрим другую проблему – подбор кандидата на вакантное место: трёх кандидатов оценивают два эксперта, каждый по своим двум критериям, а затем докладывают свои выводы руководству для принятия окончательного решения. В этом случае иерархия будет выглядеть следующим образом.
Полученная иерархия соответствует 4-х уровневой неполной иерархии с фокусом ПР. Но её можно свести к набору из двух полных трёхуровневых иерархий и одной двухуровневой: для этого нужно разрезать связи между фокусом и элементами С1 и С2.
Вывод: анализ неполных иерархий можно свести к анализу набора соответствующих полных иерархий.
Наиболее полные иерархии возникают при анализе проблем стратегического планирования. Стратегическое планирование – процесс формирования вероятностного будущего.
Уровни, возникающие при этом планировании следующие:
1. Устанавливается фокус проблемы
2. Устанавливаются экономические, политические и социальные причины, которые могут влиять на исход (иногда этот уровень опускают, переходя сразу к третьему)
3. Люди и организации (акторы), которые решают, какие действия, влияющие на экономическую, политическую и социальную ситуацию, предпринимать. К этому же уровню относятся и те, на кого влияют принимаемые решения.
4. Устанавливает цели каждого актора.
5. Средства достижения целей, которыми пользуются акторы (необязательный уровень)
6. Исходы, за которые борется каждый актор, как за результат реализации своих целей.
7. Обобщённый сценарий, который представляет собой результат реализации всех сценариев предыдущего уровня с учётом их веса. Обобщённый сценарий называется также логическим исходом.
Очень важным с точки зрения анализа иерархий является измерение весов элементов иерархии на одном уровне, чтобы можно было выделить , наиболее важные критерии , акторов и т.д. и в конце концов определить альтернативу, имеющую, в соответствии с проведёнными сравнениями наибольший вес. При этом необходимо также учитывать согласованность таких измерений.
Измерять веса можно двумя способами – сравнивая с эталоном и сравнивая попарно, чтобы распределить по весу (привести пример с взвешиванием предметов). Для ранжирования лучше второй способ.
В процессе любых измерений возможны погрешности, что, в конечном счёте, может привести к несогласованности выводов. Под согласованностью понимают следующее: если сравниваются по весу три предмета и предмет 1 оказался в четыре раза тяжелее второго, а третий в два раза тяжелее второго, то при сравнении первого и третьего важно получить не просто тяжелее, а тяжелее в восемь раз. На примере качественного сравнения показателей: что и во сколько раз лучше, может оказаться очень важным выбор шкалы и знание оценивающим предмета оценки. Как правило, чем лучше человек знаком с ситуацией, тем последовательнее в своих оценках. Обратное утверждение не всегда верно.
Следовательно, для получения хороших результатов требуется использовать подходящую численную шкалу сравнений и определять степень несогласованности суждений.
Шкалирование. Как уже упоминалось в начале курса, в связи с особенностями человеческого мышления, лучше использовать для сравнения не более 7±2 объекта. Если таких объектов больше, то необходимо попробовать сгруппировать их. Затем сравнивать группы, а затем объекты внутри группы, если это необходимо.
Наиболее распространённой на сегодняшний день в методе анализа иерархий является следующая шкала:
· Если объект А и В одинаково важны, то их отношение записывается в виде 1
· Если А незначительно важнее В, то в качестве отношения А/В используют 3 (слабое предпочтение)
· Если А значительно важнее В – 5 (предпочтительнее)
· Если А явно важнее В (сильное предпочтение) – 7
· Если А по своей значимости абсолютно предпочтительнее В -9.
Такая шкала появилась в результате большой работы многих специалистов из различных областей знаний и была проверена на многих практических задачах, где давала очень хорошие результаты.
Числа 2, 4, 6 и 8 используются для облегчения компромисса между оценками. Можно попросить провести сравнение каких-либо объектов по этой шкале и попытаться проверить согласованность оценок.
Понятно, что эти оценки различны для разных людей.
8. Математический аппарат метода анализа иерархий.
Одним из способов практического сравнения объектов, действий или обстоятельств для их количественной оценки является построение матрицы (таблицы) попарных сравнений. Пусть даны объекты А, В, С и т.д. Рассмотрим матрицу попарных сравнений этих объектов
| А | В | С | … | |
| А | а11 | а12 | а13 | … |
| В | а21 | а22 | а23 | … |
| С | а31 | а32 | а33 | … |
| … | … | … | … | … |
В этой таблице а12 –отношение важности объекта А по сравнению с В, а13— отношение важности объекта А по сравнению с С и т.д.
Вспомним несколько определений из курса математики.
Матрица А называется положительной, если:
Матрица А называется обратносимметричной, если:
Матрица А является согласованной, если:
Собственным вектором матрицы A называется такой ненулевой вектор , что для некоторого :
Собственным значением матрицы A называется такое число , для которого существует собственный вектор , то есть уравнение имеет ненулевое решение .
Теорема. Положительная обратносимметричная матрица согласована тогда и только тогда, когда ,где -максимальное собственное значение матрицы, а n-размерность матрицы.
Проанализируем свойства идеальной матрицы парных сравнений (то есть все соотношения оценены идеально).
1. Для любого i справедливо аii=1(диагональный элемент, расположенный на пересечении i-ой строки и i-го столбца), так как это отношение элемента по важности к самому себе.
2. Для любых i и k справедливо равенство аki* аik=1. Действительно, если аki – отношение веса k-го элемента (wk) к весу i-го элемента (wi), а аik –обратное отношение, то получаем аki* аik= (wk / wi)*( wi/ wk)=1. Это соответствует определению обратносимметричной матрицы. То есть для нашей матрицы попарных сравнений, если объекты оценены верно, то а21=1/ а12 и т.д.
3. Для любых i, k и l справедливо равенство аik* аkl=ail. Это как раз отражает, то, что мы говорили ранее о согласованности измерений.
4. Столбец с весами элементов является собственным вектором матрицы попарных сравнений, с собственным значением l равным количеству сравниваемых элементов (n). Если обозначить матрицу А, столбец с весами w, то будет справедливо А*w =n*w.
Если матрица попарных сравнений строится не на точных измерениях, а на субъективных суждениях, то она, естественно, может отклоняться от идеальной. В этом случае у матрицы будет несколько собственных значений. Вспомним несколько полезных для нас свойств матриц: А*w =l*w, где l=
Объединяя эти результаты, находим, что если диагональ матрицы А состоит из единиц и А – согласованная матрица, то при малых изменениях в значениях аik наибольшее собственное значение lmax остаётся близким к n (при этом всегда lmax³n), а остальные собственные значения – близкими к нулю.
Поэтому можно сформулировать следующую задачу: если А – матрица значений парных сравнений, то для нахождения вектора весов (или приоритетов) нужно найти вектор w (неравный нулю), который удовлетворяет матричному уравнению А*w =lmax*w
Для определения собственного значения lmax необходимо решить характеристическое (алгебраическое n-го порядка) уравнение
½А — lmax *Е½=0, где Е – единичная матрица и с учётом соотношения lmax³n. Далее с найденным значением lmax следует определить решение w матричного уравнения
А*w =lmax*w, то есть собственный вектор матрицы А.
Так как желательно иметь нормализованное решение, то слегка изменим w, заменив вектор w на вектор w=w/å wi. Это преобразование обеспечивает единственность вектора и для компонент преобразованного вектора åwi=1. Условие нормировки весов удобно использовать для контроля правильности расчётов весов wi.
Для проведения парных сравнений n объектов или действий требуется суждений о парных сравнениях.
Можно оценить отклонение от согласованности матрицы сравнений разностью , разделенной на (n-1). Насколько плоха согласованность для определенной задачи, можно оценить путем сравнения полученного нами значения величины с её значением из случайно выбранных суждений и соответствующих обратных величин матрицы того же размера.
Выражение называется индексом согласованности (ИС).
Индекс согласованности сгенерированной случайным образом по шкале от 1 до 9 обратносимметричной матрицы с соответствующими обратными величинами элементов, назовем случайным индексом (СИ).
В Национальной лаборатории Окриджа сгенерировали средние СИ для матриц порядка от 1 до 15 на базе 100 случайных выборок. Как и ожидалось, СИ увеличивались с увеличением порядка матрицы. Вычисления были повторены в школе Уортона для величины случайной выборки 500 в матрицах порядка до 11х11, а далее использовались предыдущие результаты для n=12, 13, 14, 15. Ниже представлены порядок матрицы и средние СИ, определенные так, как описано выше:
| 2. | 3. | 4. | 5. | 6. | 7. | 8. | 9. | 10. | 11. | 12. | 13. | 14. | 15. |
| 0,00 | 0,58 | 0,90 | 1,12 | 1,24 | 1,32 | 1,41 | 1,45 | 1,49 | 1,51 | 1,48 | 1,56 | 1,57 | 1,59 |
Отношение ИС к среднему СИ для матрицы того же порядка называется отношением согласованности (ОС). Значение ОС, меньшее или равное 0,10, будем считать приемлемым. Для идеально согласованной матрицы ОС=0, так как ИС=0.
Из таблицы для СИ видно, что матрица парных сравнений с n=2 всегда идеально согласована. Действительно, матрица А в этом случае имеет вид А = .
Найдём её собственные значения, решая соответствующее характеристическое уравнение (1-lmax) 2 =1. Получаем l1=0; l2=2. То есть lmax=2, следовательно, любая матрица парных сравнений 2-го порядка идеально согласована.
Если ОС>0,1, то имеется рассогласование элементов матрицы парных сравнений. И это характеризует уровень доверия к полученным результатам. Чем больше это отличие, тем меньше доверие. То есть желательно вернуться к этапу экспертных парных сравнений и постараться устранить или уменьшить рассогласование за счёт более тщательной оценки результатов парных сравнений.
Рассогласованность матрицы парных сравнений может быть вызвана, по крайней мере, двумя факторами:
· личными качествами эксперта
· степенью неопределенности объекта оценки
Таким образом, эта модификация метода парных сравнений содержит внутренние инструменты позволяющие определить качество обрабатываемых данных и степень доверия к ним. Эта особенность данной методики выгодно отличает его от большинства обычно применяемых при исследовании рынка методов.
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Увлечёшься девушкой-вырастут хвосты, займёшься учебой-вырастут рога 9913 — 

193.124.117.139 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
источник
По шагам расписан расчет коэффициентов значимости подходов к оценке при определении итоговой величины стоимости бизнеса.
Задача. Методом анализа иерархий обосновать коэффициенты значимости (удельные веса) доходного, затратного, сравнительного подходов к оценке стоимости бизнеса для определения итоговой величины стоимости.
Решение. Расчет коэффициентов значимости методом анализа иерархий основан на выделении следующих параметров в качестве критериев сравнения подходов к оценке:
- А. возможность отразить действительные намерения продавца;
- Б. тип, качество, обширность данных, на основе которых проводится анализ;
- В. способность параметров используемых методов учитывать конъюнктурные колебания;
- Г. способность учитывать специфические особенности объекта, влияющие на его стоимость (местонахождение, размер, потенциальная доходность).
Нумерация формул, термины и этапы применения метода анализа иерархий рассмотрены выше (для просмотра перейдите по указанной активной ссылке).
Первоначально построена следующая матрица сравнения и рассчитаны значения приоритетов критериев.
Таблица 5 — Матрица сравнения и рассчитаны значения приоритетов критериев
| А | Б | В | Г | Средние геометрические | Нормализованный вектор приоритетов (НВП) – Вес критерия (расчет по формуле (2)) | ||||
| А | 1 | ½ | 3 | 2 | (1 ×1/2 × 3 ×2) 1/4 = | 1,32 | 1,32 /4,27 = | 0,31=НВПА | |
| Б | 2 | 1 | 3 | 1 | (2 ×1 × 3 × 1) 1/4 = | 1,57 | 1,57/4,27 = | 0,37=НВПБ | |
| В | 1/3 | 1/3 | 1 | 2 | (1/3 ×1/3 × 1 × 2) 1/4 = | 0,69 | 0,69/4,27 = | 0,16=НВПВ | |
| Г | 1/2 | 1 | 1/2 | 1 | (1/2 ×1 × 1/2 × 1) 1/4 = | 0,71 | 0,71/4,27 = | 0,17=НВПГ | |
| ИТОГО | (по формуле (1)) 4,27 | 1,00 | |||||||
| λmax(по форм.(3)) | (1+2+1/3+½)×0,31 +(1/2+1+1/3+1)× 0,37+(3+3+1+1/2)×0,16+(2+1+2+1)×0,17 = 4,41 | ||||||||
| ИС(по форм.(4)) | (4,41 — 4)/ (4 – 1) = 0,14 | ||||||||
| ОС(по форм.(5)) | 0,14/ 0,90 = 0,15 | ||||||||
Сравниваются значимости результатов, полученных затратным (З), сравнительным (С) и доходным (Д) подходами к оценке, по каждому критерию согласования:
Таблица 6 — А. возможность отразить действительные намерения продавца:
| З | С | Д | Средние геометрические | Нормализованный вектор приоритетов (НВП) – Значимость подхода (расчет по формуле (2)) | |||||
| З | 1 | 1/2 | 1/3 | (1× 1/2× 1/3) 1/3 = | 0,55 | 0,55/3,37 = 0,16 | |||
| С | 2 | 1 | 1/2 | (2 × 1 × 1/2) 1/2 = | 1,00 | 1,00/3,37 = 0,30 | |||
| Д | 3 | 2 | 1 | (3 × 2 × 1) 1/3 = | 1,82 | 1,82/3,37 = 0,54 | |||
| Сумма | (по формуле (1)) 3,37 | 1,00 | |||||||
| λmaxА(по форм.(3)) | (1+2+3)×0,16+(1/2+1+2)×0,3+(1/3+1/2+1)×0,54=2,998 | ||||||||
| ИСА(по форм.(4)) | (3-3)/ (3-1)=0 | ||||||||
| ОСА(по форм.(5)) | 0/ 0,58 = 0,01 | ||||||||
Таблица 7 — Б. тип, качество, обширность данных, на основе которых проводится анализ:
| З | С | Д | Средние геометрические | Нормализованный вектор приоритетов (НВП) – Значимость подхода (расчет по формуле (2)) | ||||
| З | 1 | 3 | 5 | (1×3×5) 1/3 = | 2,47 | 0,46/3,41 = 0,64 | ||
| С | 1/3 | 1 | 3 | (1/3 × 1 × 3) 1/3 = | 1,00 | 1,59/3,41 = 0,26 | ||
| Д | 1/5 | 1/3 | 1 | (1/5 × 1/3 × 1) 1/3 = | 0,41 | 1,36/3,41 = 0,10 | ||
| Сумма | (по формуле (1)) | 3,87 | 1,00 | |||||
| λmaxБ(по форм.(3)) | (1+3+5)×0,64+(0,33+1+3)×0,26+(0,2+0,33+1)×0,1=3,04 | |||||||
| ИСБ(по форм.(4)) | (3,04-3)/ (3-1)=0,02 | |||||||
| ОСБ(по форм.(5)) | 0/ 0,58 = 0,03 | |||||||
Таблица 8 — В. способность параметров используемых подходов учитывать конъюнктурные колебания:
| З | С | Д | Средние геометрические | Нормализованный вектор приоритетов (НВП) – Значимость подхода (расчет по формуле (2)) | |||||
| З | 1 | 1/2 | 1/2 | (1× 1/2 × 1/2) 1/3 = | 0,63 | 0,63/3,22 = 0,20 | |||
| С | 2 | 1 | 1/2 | (2 × 1 × 1/2) 1/3 = | 1,00 | 1/3,22 = 0,31 | |||
| Д | 2 | 2 | 1 | (2 × 2 × 1) 1/3 = | 1,59 | 1,59/3,22 = 0,49 | |||
| Сумма | (по формуле (1)) | 3,22 | 1,00 | ||||||
| λmaxВ(по форм.(3)) | 3,05 | ||||||||
| ИСВ(по форм.(4)) | 0,03 | ||||||||
| ОСВ(по форм.(5)) | 0,05 | ||||||||
Таблица 9 — Г. способность учитывать специфические особенности объекта, влияющие на его стоимость (местонахождение, размер, потенциальная доходность):
| З | С | Д | Средние геометрические | Нормализованный вектор приоритетов (НВП) – Значимость подхода (расчет по формуле (2)) | |||||
| З | 1 | 2 | 3 | (1× 2 × 3) 1/3 = | 1,82 | 1,82/3,32 = 0,55 | |||
| С | ½ | 1 | ½ | (1/2 × 1 × 1/2) 1/3 = | 0,63 | 0,63/3,32 = 0,19 | |||
| Д | 1/3 | 2 | 1 | (1/3 × 2 × 1) 1/3 = | 0,87 | 0,87/3,32 = 0,26 | |||
| Сумма | (по формуле (1)) | 3,32 | 1,00 | ||||||
| λmaxГ(по форм.(3)) | 3,14 | ||||||||
| ИСГ(по форм.(4)) | 0,07 | ||||||||
| ОСГ(по форм.(5)) | 0,12 | ||||||||
Таблица 10 — Расчет итоговых значений коэффициентов значимости каждого подхода к оценке
| А | Б | В | Г | Итоговая оценка коэффициентов значимости и общий приоритет для каждого подхода (по формуле (6)) | ||||
| 0,31 (НВПА из табл.5) | 0,37(НВПБ из табл.5) | 0,16 (НВПВ из табл.5) | 0,17 (НВПГ из табл.5) | расчет | значение | |||
| З | 0,16 | 0,64 | 0,20 | 0,55 | 0,31×0,16+0,37×0,64+0,16×0,20+0,17×0,55 = | 0,40 | ||
| С | 0,30 | 0,26 | 0,31 | 0,19 | 0,31×0,30+0,37×0,26+0,16×0,31+0,17×0,19 = | 0,27 | ||
| Д | 0,54 | 0,10 | 0,49 | 0,26 | 0,31×0,54+0,37×0,10+0,16×0,49+0,17×0,26 = | 0,33 | ||
| ИС | (ИСА из табл.6) | 0,02(ИСБ из табл.7) | 0,03(ИСВ из табл.8) | 0,07(ИСГ из табл.9) | сумма | 1,00 | ||
| ОИС (по формуле (7)) | 0,31×0 + 0,37×0,02 + 0,16×0,03 + 0,17×0,07 = 0,024 | |||||||
| ООС (по формуле (8)) | 0,024/ 0,58 = 0,04 | |||||||
Ответ: коэффициент значимости (удельный вес) стоимости по затратному подходу равен 0,40, по сравнительному — 0,27, по доходному — 0,33.
По представленному решению остались вопросы? Тогда купите описанное на этой странице решение задачи в файле Excel ! Для приобретения данного файла за 50 руб. напишите прямо сейчас по адресу . Перейдите по следующей ссылке и узнайте, как купить электронные материалы на данном сайте.
источник
· иерархическое представление проблемы
· метод сравнения объектов относительно стандартов
· многокритериальный выбор в иерархиях с различным числом и составом альтернатив под критериями
· общая характеристика подхода метода анализа иерархий
Метод анализа иерархий (Analytic Hierarchy Process — AHP), или подход аналитической иерархии предполагает декомпозицию проблемы на простые составляющие части и обработку суждений ЛПР. В результате определяется относительная значимость исследуемых альтернатив для всех критериев, находящихся в иерархии. Относительная значимость выражается численно в виде векторов приоритетов. Полученные таким образом значения векторов являются оценками в шкале отношений и соответствуют так называемым жестким оценкам.
Постановка задачи, решаемой с помощью метода AHP, заключается обычно в следующем.
Дано: общая цель решения задачи; критерии оценки альтернатив; альтернативы. Требуется: выбрать наилучшую альтернативу.
Подход AHP состоит из совокупности этапов:
1. Структуризация задачи виде иерархической структуры с несколькими уровнями: цели – критерии – альтернативы.
2. Попарное сравнение элементов каждого уровня лицом, принимающим решения. Результаты сравнения имеют числовой характер.
3. Вычисление коэффициентов важности для элементов каждого уровня. Проверка согласованности суждений ЛПР.
4. Подсчет количественной оценки качества альтернатив. Выбор лучшей альтернативы.
Построение иерархии начинается с очерчивания проблемы исследования. Далее строится иерархия, включающая цель на верхнем уровне, промежуточные уровни (например, критерии) и альтернативы, формирующие самый нижний иерархический уровень (рисунок 3).
Рис. 3. Иерархическое представление проблемы
Верхний индекс у элементов указывает уровень иерархии, а нижний – их порядковый номер.
Рассмотрим процесс построения иерархической структуры на примере.
Пример: В современном мире для эффективного руководства необходимо иметь максимум информации, причем оперативной и постоянно обновляемой, также необходимо быстро принимать решения и с оптимальной скоростью притворять их в жизнь, доводить до подчиненных. В связи с этим современный бизнес просто немыслим без передовых средств связи, в частности, мобильного телефона. Телефон стал неотъемлемым атрибутом делового человека.
Для эффективного использования сотовой связи необходимо правильно выбрать оператора связи. При выборе оператора нужно учесть ряд критериев:
· доступность в любое время, в любом месте;
· спектр предоставляемых дополнительных услуг;
Учитывая все это, структура решаемой проблемы: выбор оператора связи из имеющихся на рынке, — может быть представлена в виде иерархической структуры, представленной на рисунке 4.
 |
Рис. 4. Иерархическая схема проблемы выбора оператора сотовой связи
Во многих случаях на уровне альтернатив должны быть указаны цифры. Необходимо сопоставить эти зачастую совершенно разнородные величины так, чтобы выявить предпочтения ЛПР. После построения иерархии устанавливается метод сравнения ее элементов. Существует несколько методов сравнения элементов, выбор которых обусловлен характером связей альтернатив с уровнем критериев, количеством альтернатив, временем поступления альтернатив и прочими соображениями ЛПР.
Для установления относительной важности элементов иерархии используется шкала отношений. Данная шкала позволяет ЛПР ставить в соответствие степеням предпочтения одного сравниваемого объекта перед другим некоторые числа (таблица 2).
Таблица 2. Шкала отношений
Два действия вносят одинаковый вклад в достижение цели
Некоторое преобладание значимости одного действия над другим
Существуют соображения в пользу предпочтения одного из действий, однако эти соображения недостаточно убедительны
Существенная или сильная значимость
Имеются надежные данные или логические суждения для того, чтобы показать предпочтительность одного из действий
Очевидная или очень сильная значимость
Убедительное свидетельство в пользу одного действия перед другим
Свидетельства в пользу предпочтения одного действия перед другим в высшей степени убедительны
Промежуточные значения между двумя соседними суждениями
Ситуация, когда необходимо компромиссное решение
Обратные величины приведенных выше величин
Если действию i при сравнением с действием j приписывается одно из определенных выше чисел, то действию j при сравнении с действием i приписывается обратное значение
Если согласованность была постулирована при получении N числовых значений для образования матрицы
При использовании указанной шкалы ЛПР, сравнивая два объекта в смысле достижения цели, расположенной на вышележащем уровне иерархии, должен поставить число в интервале от 1 до 9 или обратное значение.
Для этого в иерархии выделяют элементы двух типов: элементы – родители и элементы – потомки. Элементы – потомки воздействуют на соответствующие элементы вышестоящего уровня иерархии, являющиеся по отношению к первым элементами – родителями. Матрицы парных сравнений строятся для всех элементов – потомков, относящихся к определенному родителю. Парные сравнения производятся в терминах доминирования одного элемента над другим в соответствии со шкалой отношений.
Если элемент Е1 доминирует над элементом Е2, то клетка матрицы, соответствующая строке Е1 и столбцу Е2, заполняется целым числом, а клетка, соответствующая строке Е2 и столбцу Е1, заполняется обратным к нему числом.
При проведении парных сравнений следует отвечать на вопросы: какой из двух сравниваемых элементов важнее или имеет большее воздействие, какой более вероятен и какой предпочтительнее.
При сравнении критериев обычно спрашивают, какой из критериев более важен; при сравнении альтернатив по отношению к критерию – какая из альтернатив более предпочтительна или более вероятна.
Рассмотрим процесс построения матрицы парных сравнений не примере.
Пример. Провести анализ провайдеров на предмет их желательности с точки зрения определенного человека. Этот человек, руководствуется пятью независимыми (будем считать что это так) характеристиками: тарифы, скорость сети, доступность сети, удобство оплаты, дополнительные услуги. В качестве альтернатив человек рассматривает следующие компании: Comstar, Зебра Телеком, РОЛ и МТУ.
Иерархическая схема может быть представлена следующим образом (рисунок 5):
 |
Рис. 5. Иерархическая схема проблемы выбора провайдера
После построения иерархии строятся матрицы парных сравнений. При сравнении элементов, принадлежащих одному уровню иерархии, ЛПР выражает свое мнение, используя одно из приведенных в таблице 2 определений. В матрицу сравнений заносится соответствующее число.
Начнем построение матриц парных сравнений с матрицы «Удовлетворение провайдером», которая покажет относительную важность характеристик при выборе компании.
При построении матрицы человек задавался вопросом, какая характеристика для него наиболее важна при выборе провайдера.
При сравнении любого критерия с самим собой не возникает вопросов о доминирующем воздействии одного из критериев, т. е. соответствующая позиция в матрице заполняется единицей, что соответствует одинаковой степени значимости критериев (см. таблицу 2 – шкала отношений).
Рассмотрим первую строку матрицы. В позиции один два, при сравнении важности тарифов и скорости, ЛПР поставил значение равное 
Цифра пять в позиции один три говорит о том, что для ЛПР тарифы важней доступности сети, в то время 
Иерархию в какой-либо рассматриваемой проблеме можно выявить посредством анкетирования, синтезировать результат и продолжить дело с помощью анкеты для выявления суждений.
Рассмотрим, как могут быть получены матрицы суждения для одной матрицы. Тот же метод может быть применен для иерархии. В качестве примера возьмем иерархическую структуру, представленную на рисунке 6.
 |
Рис. 6 Иерархическая схема задачи выбора нового сотрудника
Обозначим значения шкалы, располагая их в ряд от одного крайнего значения к равенству и затем вновь повышая до второго крайнего значения (таблица 3). В левом столбце перечисли все альтернативы, которые нужно сравнивать по степени превосходства с другими альтернативами из правого столбца. Эксперты должны отметить суждения, которые выражают превосходство элемента из левого столбца над соответствующим элементом из правого столбца, расположенном в той же строке. Если такое превосходство в действительности имеет место, то одна из позиций левее равенства будет отмечена. В противном случае будет отмечено равенство или некоторая позиция справа.
Таблица 3. Сравнение альтернатив относительно критерия «образование»
Такая таблица составляется и заполняется для каждого критерия (четыре анкеты для сравнения альтернатив по каждому из критериев) и для сравнения критериев относительно цели (одна анкета в которой ЛПР решает какие критерии для него наиболее значимые).
После заполнения экспертами анкет, по ним составляются матрицы парных сравнений. Например анкета имеет вид, представленный в таблице 4:
Таблица 4. Сравнение альтернатив относительно критерия «образование», составленное первым экспертом по резюме кандидатов
Матрица парных сравнений для анкеты из таблицы 4 имеет вид:
Для агрегирования мнений экспертов принимается среднегеометрическое, вычисляемое по следующей формуле:
Логичность критерия становится очевидной, если два равноценных эксперта указывают при сравнении объектов соответственно оценки 

В достаточно ответственных задачах при оправданных задачах на экспертизу осреднение суждений экспертов проводится с учетом их квалификации. Для определения весовых коэффициентов экспертов используют иерархическую структуру критериев, представленную на рисунке 7.
 |
Рис. 7 Иерархия для ранжирования экспертов
Расчет агрегированной оценки в случае привлечения 
Пример. Предположим, что в случае с выбором нового кандидата на работу, первый эксперт, которым мог быть начальник отдела управления кадрами, по результатам резюме заполнил анкету, которая приведена в таблице 4. Во время проведения собеседования с каждым из претендентов, второй эксперт, например один из директоров, заключил, что по уровню образования кандидатам соответствует анкета, заполненная следующим образом (таблица 5):
Таблица 5. Сравнение альтернатив относительно критерия «образование», составленное вторым экспертом по результатам собеседования с кандидатами
Матрица парных сравнений для анкеты в таблице 5, имеет вид:
Для объединения оценок суждений двух экспертов строится матрица с средним геометрическим оценок. В данной задаче такой подход не совсем правомерен. Однако, будем считать что суждения двух экспертов обладают одинаковой степенью значимости. Результирующая матрица имеет вид:
При построении матриц парных сравнений важным вопросом является согласованность, или однородность матрицы. Согласованность – это следование логике при высказывании суждений экспертом. Для более наглядной иллюстрации понятия «согласованности» приведем пример.
Пример. Предположим, что имеется три фрукта: яблоко, апельсин и ананас. Некто, предположим ребенок, говорит следующее: «Ананас в три раза вкуснее апельсина, а апельсин в два раза вкуснее яблока». Следующим высказыванием ребенка на вопрос о его любви к яблокам и ананасам, он говорит, что ананас в пять раз лучше яблока. В таких высказываниях ребенка несогласованности практически нет, несмотря на то, что исходя из его первого предложения ананас в шесть раз предпочтительнее яблока. Однако, нарушения логики могло быть гораздо более серьезным и даже привести к нетранзитивности. Так, второе высказывание могло звучать: «Мне яблоки нравятся больше чем ананасы».
В практических задачах количественная и транзитивная (порядковая) однородность нарушается, поскольку человеческие ощущения нельзя выразить точной формулой. Для улучшения однородности в числовых суждениях, какая бы величина 




Определение. Квадратную матрицу 

При построении матриц парных сравнений не следует искусственно выстраивать матрицу исходя из условий согласованности. Такой подход может исказить предпочтения ЛПР. Однако во многих задачах, однородность матриц должна быть высокой. Для оценки однородности используют то свойство, что при нарушении однородности ранг матрицы отличен от единицы и она имеет несколько собственных значений. При небольших отклонениях суждения от однородности одно из собственных значений будет существенно большие остальных и приблизительно равно порядку матрицы. Это свойство вытекает из следующих двух теорем.
Теорема 1. В положительной обратносимметрической квадратной матрице 
Теорема 2. Положительная обратносимметрическая квадратная матрица А согласованна тогда и только тогда, когда 
Таким образом, для оценки однородности суждений эксперта можно использовать отклонение величины максимального собственного значения 

Согласованность суждения оценивается индексом однородности (индексом согласованности) или отношением однородности (отношением согласованности) в соответствии со следующими формулами:

Таблица 6. Среднее значение индекса однородности в зависимости от порядка матрицы
источник
Изложение алгоритма МАИ приведем, следуя [1] и [5], для наглядности совместив формальное описание с примером.
Метод анализа иерархий является систематической процедурой для иерархического представления компонентов, определяющих суть любой проблемы. Метод состоит в декомпозиции проблемы на все более простые составляющие части и дальнейшей обработке последовательности суждений лица, принимающего решение (ЛПР), по парным сравнениям. В результате может быть выражена относительная степень взаимодействия элементов. Эти суждения затем выражаются численно. Метод анализа иерархии включает процедуры синтеза множественных суждений, выявления приоритетности критериев и нахождения альтернативных решений. Полученные таким образом значения являются оценками в шкале отношений и соответствуют некоторым численным оценкам.
Решение проблемы – это процедура поэтапного установления приоритетов. На первом этапе выявляются наиболее важные компоненты проблемы, на втором – наилучший способ проверки наблюдений, испытания и оценка альтернатив; на следующем этапе вырабатывается решение и оценивается его качество. Процесс может быть проведен также над последовательностью иерархий: в этом случае результаты, полученные в одной из них, используются в качестве входных данных при изучении следующей. Метод многокритериального отбора систематизирует процесс решения такой многоступенчатой задачи.
1. Принцип идентичности и декомпозиции. Предусматривает структурирование проблем в виде иерархии или сети.
2. Принцип сравнительный суждений (парных сравнений). Предполагает, что элементы задачи (альтернативы и критерии) сравниваются попарно с позиции их воздействия на общую характеристику.
3. Принцип синтеза приоритетов. Предполагает формирование набора локальных приоритетов, которые выражают относительное влияние множества элементов на элемент примыкающего сверху уровня.
Целью задачи является строительство аэропорта [3]. Необходимо выбрать лучшую площадку для строительства аэропорта с точки зрения выделенных критериев. Комиссия по выбору постройки аэропорта предварительно отобрала из нескольких возможных три альтернативных варианта площадок – А1, А2, А3. Было выявлено три основных критерия, влияющих на принятие решения о выборе площадки для строительства: 1 – стоимость строительства, 2 – время в пути от аэропорта до центра города, 3 – количество жителей, подвергающихся шумовым воздействиям. При решении задачи используется МАИ для поддержки процесса принятия решений.
Этап 1. Построение иерархической структуры задачи многомерного выбора.
В общем случае простейшей трехуровневой иерархии структура имеет вид Рис.1.
Рис. 1. Обобщенна иерархическая структура проблемы
Структуру решаемой задачи можно представить в виде иерархической структуры, показанной на Рис. 2.
Рис. 2. Иерархическая структура проблемы
Этап 2. Выполнение попарных экспертных сравнений элементов каждого уровня иерархий.
Рассмотрим элементы С1, С2, …, Сn некоторого зафиксированного уровня иерархи. Мы хотим определить веса ѡ1, ѡ2, …,ѡn влияния этих элементов на некоторый элемент вышестоящего уровня. Основным инструментом оценки влияния является матрица чисел по шкале отношений 1, …, 9 (табл. 1), представляющих суждения о парных сравнениях. Для представления приоритетов в МАИ выбран собственный вектор, принадлежащий наибольшему собственному значению указанной матрицы А. Обозначим через 
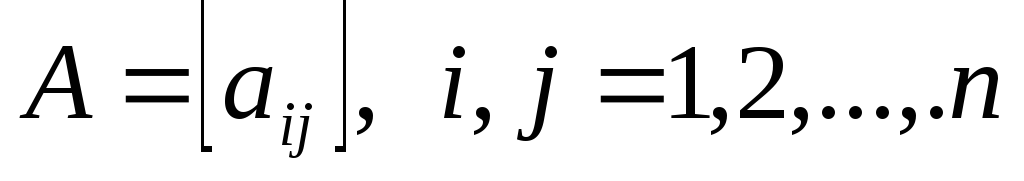
Матрица А с содержательной точки зрения будет согласованной по оценкам при введении условия
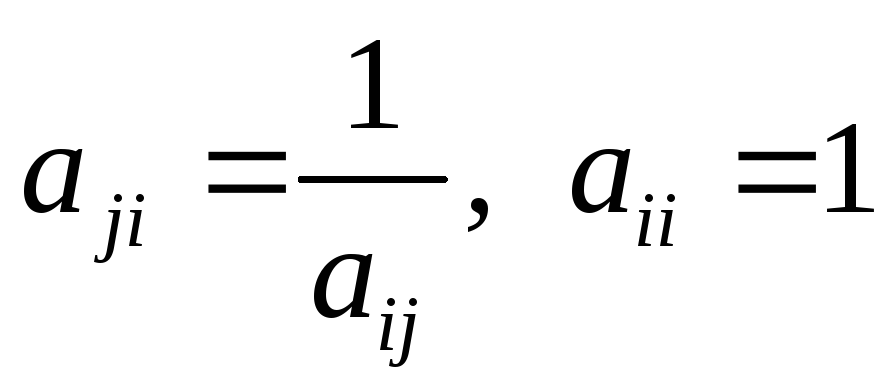
С математической точки зрения это условие наделяет матрицу А свойством обратносимметричной матрицы. На главой диагонали матрицы А стоят 1.
Если оценки попарных сравнений известны точно, т.е. оценки основаны на экспериментальных измерениях, то
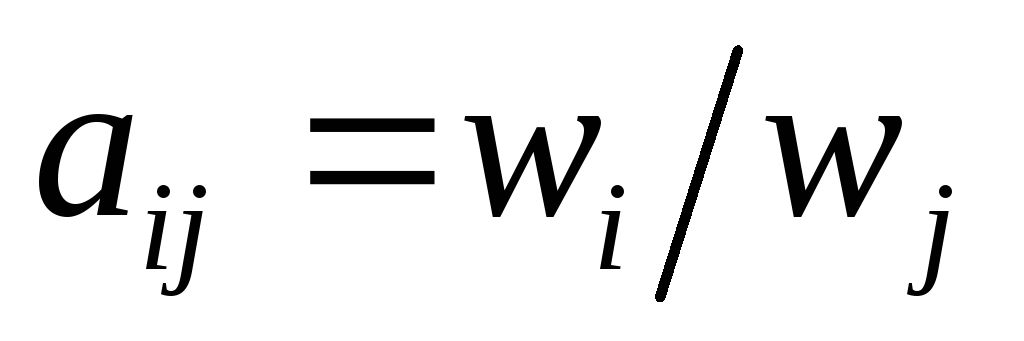
т.е. веса влияния элементов известны.
Например, если взвешиваются два предмета: С1=305,2 и С2=244,2, тогда отношение 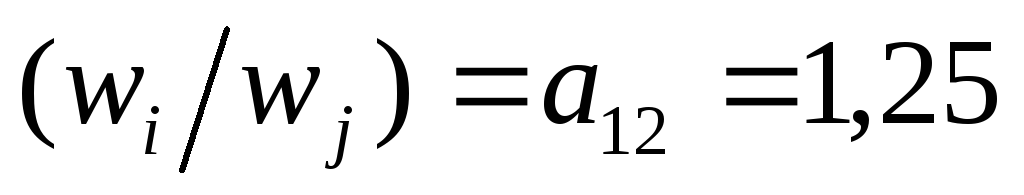
Для случая экспериментального измерения весов ѡ1, ѡ2, …,ѡi,…, ѡn сравниваемых элементов на уровне иерархии согласованность считается полной, естественно, с точностью до погрешности измерительных приборов или расчетных методик. При экспертной оценке отношений (7) согласованность суждений и соответственно матрицы А будет не полной. Значит нужно разработать некоторую числовую меру отклонения согласованности матрицы А от идеальной (см. ниже формулу отношения согласованности (9)).
Теперь рассмотрим подробнее содержательный смысл требования согласованности в МАИ.
В МАИ под согласованностью суждений подразумевается не просто традиционное требование транзитивности предпочтений [3]: если например, для индивидуума яблоки предпочтительнее апельсинов, а апельсины предпочтительнее бананов, то яблоки должны быть предпочтительнее бананов.
Схематически это можно записать так:
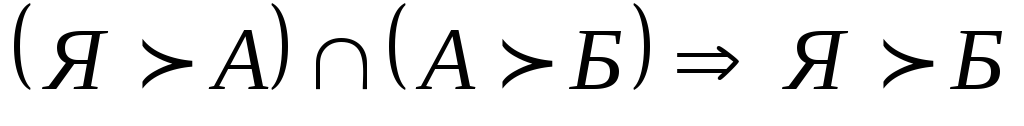

В МАИ транзитивность наделяется количественными отношениями. Например, если яблоки в 2 раза предпочтительнее апельсин ( по цене), а апельсины предпочтительнее бананов в 3 раза, то яблоки должны быть в 6 раз предпочтительнее бананов. Именно это автор МАИ Саати называет числовой (кардинальной) согласованностью предпочтений. Несогласованность означает отсутствие пропорциональности, которое может нарушить транзитивность.
МАИ не только показывает наличие несогласованности отдельных сравнений, но и дает численную оценку того, как сильно нарушена согласованность для всей рассматриваемой задачи.
Замечание. В простейшей версии МАИ считается, что элементы в каждой группе иерархии (называемой уровнем, кластером, стратой) независимы между собой, но все они влияют на каждый элемент другого (вышестоящего) уровня. Таким образом, общая задача многокритериального выбора сводится к задаче оценки влияния уровней иерархи (снизу-вверх либо сверху-вниз).
Теперь обратимся к расчетам для нашего примера.
Зафиксируем нижний (третий) уровень иерархи Рис. 2, содержащий элементы А1, А2, А3 альтернативных площадок для строительства аэропорта. Зафиксируем также один элемент К1 – стоимость строительства на уровне 2 иерархии.
Примечание: в МАИ можно формировать матрицу парных сравнений на основе любой шкалы отношений, применяемой для измеряемых свойств сравниваемых объектов. В этом случае экспертная оценка заменяется отношением двух соответствующих измерений. Новая шкала (собственный вектор), которая выводится из матрицы парных сравнений, содержащий оценки реальных измерений, будет эквивалентна той, которую можно получить путем нормирования соответствующих измерений.
Шкала относительной важности
Матрица экспертных оценок влияния элементов А1, А2, А3 на элемент К1 второго уровня иерархии показана в таблице 2 (выделено темным цветом). В таблице 2 приведены также расчетные величины для определения максимального собственного значения 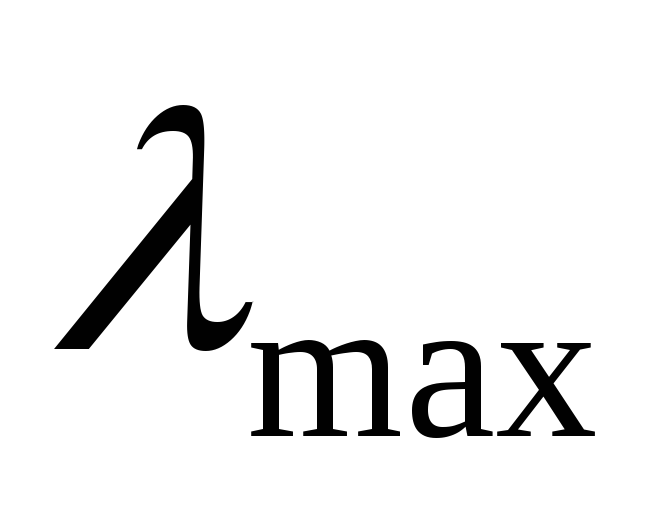
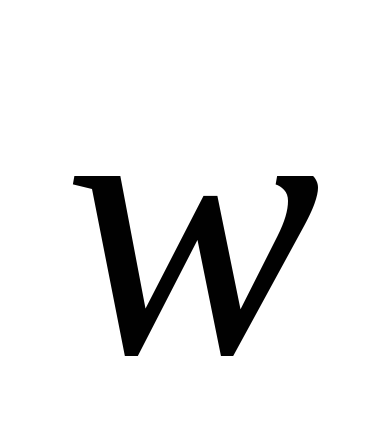
Аналогично получены матрицы парных сравнений элементов А1, А2, А3 относительно критерия К2 (таблица 3) и критерия К3 (таблица 4).
Матрица АС.1 парных сравнений альтернатив по первому критерию
Стоимость производства К1
Компоненты собственного вектора W1
Нормализованные компоненты собственного вектора приоритетов
Матрица АС.2 парных сравнений альтернатив по второму критерию
Стоимость производства К2
Компоненты собственного вектора W2
Нормализованные компоненты собственного вектора приоритетов
Матрица АС.3 парных сравнений альтернатив по третьему критерию
Стоимость производства К3
Компоненты собственного вектора W3
Нормализованные компоненты собственного вектора приоритетов
Аналогично строиться матрица парных сравнений для второго уровня иерархий, элементами которого являются критерии К1, К2, К3. Эта матрица показана в таблице 5 (выделено темным цветом).
Матрица АС.4 парных сравнений критериев
Компоненты собственного вектора W4
Компоненты нормализованного собственного вектора приоритетов элементов второго уровня (критериев)
Этап 3. Определение вектора приоритетов.
В качестве вектора приоритетов для каждого уровня иерархии принят нормализованный главный собственный вектор матрицы попарных сравнений. Для расчета этих векторов используется приближенный метод 4 из [1] оценки через средние геометрические.
Собственный вектор обеспечивает упорядочение приоритетов. Чем больше i-я компонента СВ, тем больше влияние i-го элемента в комплексе всех элементов анализируемого уровня иерархии на выделенный элемент С вышестоящего уровня.
Для нижнего уровня альтернатив (площадок для строительства А1, А2, А3) алгоритм расчета собственного вектора, относящийся к матрице парных сравнений из таблицы 2, показан в таблице 6. В таблице 2 показан также результат расчета – нормализованный собственный вектор 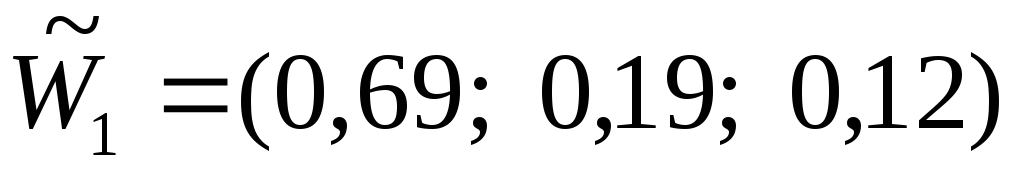
Аналогично рассчитывается нормализованные собственные векторы для матриц парных сравнений Ас.2 и Ас.3 из таблиц 3 и 4.
Получены оценки: 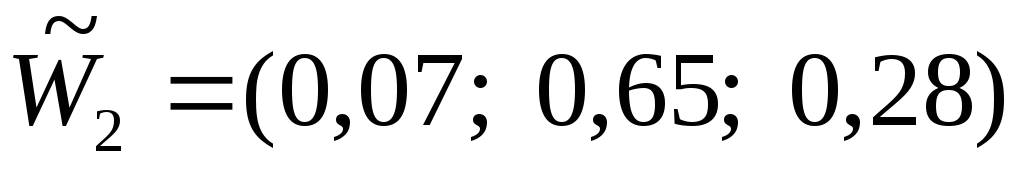
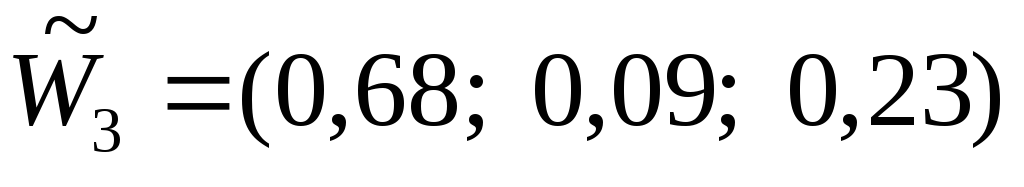
Для второго уровня иерархии, включающего критерии К1, К2 и К3, оценка нормализованного собственного вектора, характеризующие его приоритеты этого уровня по влиянию на единственный элемент верхнего (первого) уровня, т.е. цель выбора, производится по описанному выше алгоритму. Для матрицы парных сравнений Ас.4 из таблицы 5, получены данные расчета: 
Таким образом, все векторы приоритетов для второго и третьего уровней иерархии получены.
Этап 4. Определение максимальных собственных значений и степени согласованности матриц парных сравнений.
Прежде чем перейти к синтезу оптимальной альтернативы с учетом всех элементов второго и третьего уровней иерархии, нужно убедиться в достаточном уровне согласованности всех матриц суждений Ас.1, Ас.2, Ас.2, Ас.4. Для этого нужно вычислить максимальные собственные значения 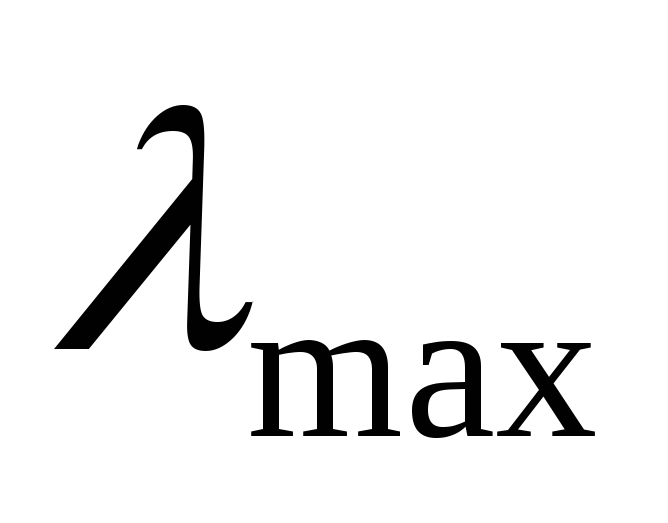

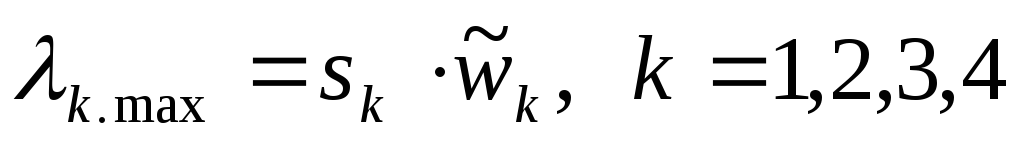

где k – номер матрицы парных сравнений (суждений); 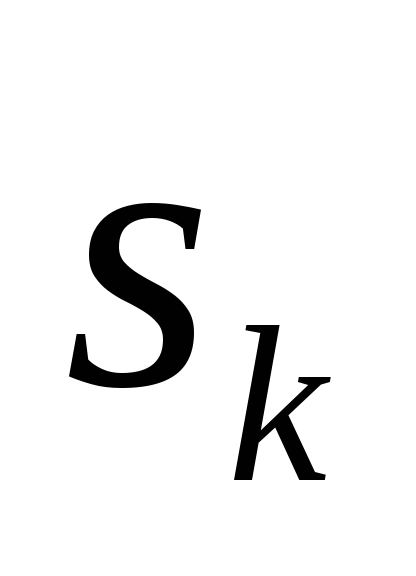
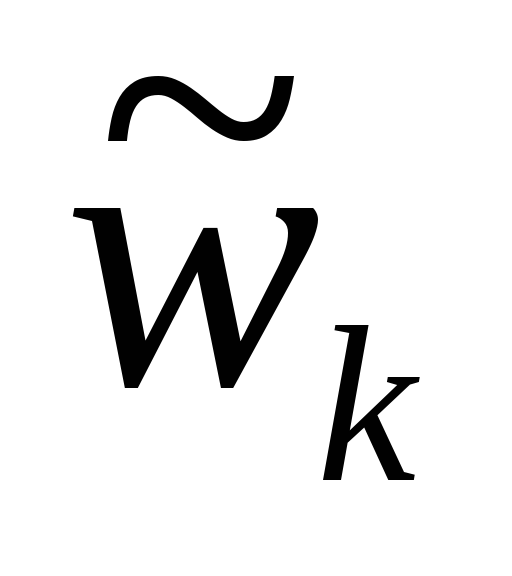
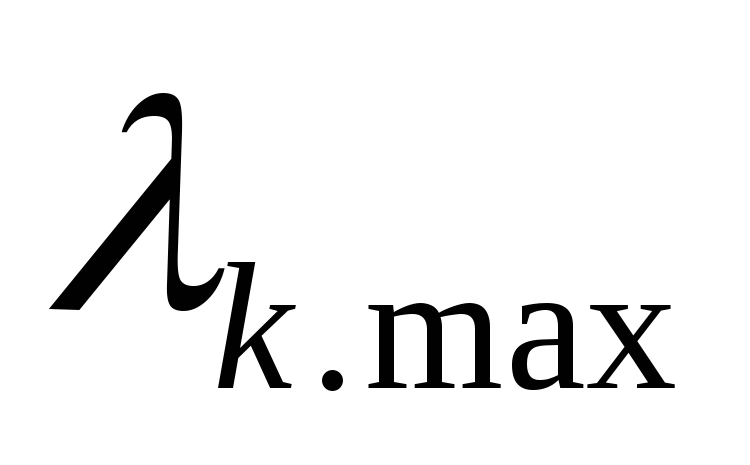
Матрица парных сравнений альтернатив по первому критерию К1
источник