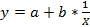Сравнение плана и факта достаточно частая задача в бизнес-среде.
Рассмотрим различные виды план-факт анализа в Excel и способы их создания.
Наиболее популярными видами сравнения являются таблицы и диаграммы.
Таблицы удобно использовать, если сравнение между планом и фактом происходит по различным показателям, например, данные по продажам различных товаров компании, P&L, CF и т.д.
Диаграммы удобнее для визуализации план-факта конкретного показателя, например, месячная динамика продаж конкретного товара.
Стандартная план-факт таблица состоит из нескольких блоков: в левой части — название показателя, в центре — данные с планом и фактом, в правой — отклонение (в абсолютных величинах, в процентах).
Для лучшей визуализации дополнительно можно окрашивать ячейку или шрифт текста с отклонением, например, в красный и зеленый цвета.
Предположим, что для план-факт графика у нас имеются помесячные данные по продажам (фактические и планируемые), а также отклонение между фактом и планом:
Разберем 2 различных варианта построения план-факт диаграмм.
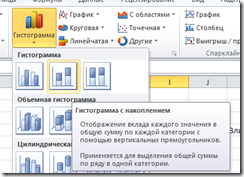
Выделяем диапазон ячеек A1:M4 и добавляем стандартный график с маркерами (на панели вкладок выбираем Вставка -> График -> График с маркерами):
На графике отобразились 3 ряда — Факт, План и Отклонение, при этом ряд с отклонением получился существенно ниже первых двух за счет эффекта масштаба.
Поэтому сделаем ряд «Отклонение» гистограммой (нажимаем правой кнопкой мыши на ряд, выбираем Изменить тип диаграммы -> Гистограмма -> Гистограмма с группировкой) и перенесем его на вспомогательную ось (снова выбираем ряд, нажимаем правую кнопку и выбираем Формат ряда данных -> Параметры ряда -> По вспомогательной оси)
Теперь приведем в порядок внешний вид план-факт диаграммы — скроем вспомогательную ось, установим минимальные и максимальные значение для основной и вспомогательной оси:
Добавляя подпись данных к рядам получаем окончательный вид план-факт графика:
Еще одним вариантом план-факт анализа является диаграмма с использованием свойств полосы повышения-понижения.
Повторяем действия из первого примера, выделяем диапазон ячеек A1:M3 (без отклонения) и строим график с маркерами:
Во вкладке Конструктор (Excel 2013 и старше) или Макет (Excel 2007-2010) добавляем Полосы повышения-понижения:
Между линией факта и плана появились прямоугольные полосы (полосы повышения-понижения), которые показывают изменение между линиями.
При этом в зависимости от знака отклонения они окрашиваются в разные цвета (в данном примере, если факт больше плана, то в черный и наоборот, если факт меньше плана, то в белый).
Изменим цвет полосы повышения на зеленый, а полосы понижения на красный, а также сделаем их полупрозрачными, чтобы полосы не наезжали на линии графика (нажимаем правой кнопкой мыши на полосу и выбираем Формат полос повышения/понижения):
Подробно ознакомиться с шаблонами диаграмм из разобранных примеров — скачать пример.
источник
Многие показатели работы компании являются многофакторными, поскольку зависят сразу от нескольких параметров, связь между которыми не всегда очевидна. В таких случаях применяют факторный анализ. Это статистический метод анализа параметра на основе обнаружения количественных связей между разными параметрами. Методику и расчетные примеры можно найти в статье.
| параметр | прошлый период | исследуемый период | изменение прибыли | |
| в абсолютных значениях | в относительных значениях, % | |||
| объем продаж | 10000 | 10500 | 500 | 5,0 |
| себестоимость единицы | 500 | 450 | -50 | -10 |
| чистая прибыль | 1700 | 2000 | 300 | 17,6 |
| коммерческие издержки | 1400 | 1600 | 200 | 15,4 |
| управленческие издержки | 700 | 800 | 700 | 14,3 |
| индекс изменения цен | 2,00 | 2,20 | 0,20 | 10 |
Из этих данных можно сделать несколько выводов:
- Объем продаж за отчетный период увеличился на 5%.
- В том числе этому способствовало снижение себестоимости на 10%.
- С другой стороны, выросли и издержки – на 15,4% коммерческие и на 14,3% управленческие.
- Поэтому фактор снижения себестоимости на 10% не привел к аналогичному изменению дохода, который увеличился только на 5%.
В этом случае за основу берут 3 показателя – это доход, себестоимость единицы и чистая прибыль.
| параметр | объем продаж | абсолютная разница | относительная разница | |
| прошлый период | исследуемый период | |||
| доход | 70000 | 80000 | 10000 | 14,3% |
| себестоимость единицы | 65000 | 67000 | 2000 | 3,1% |
| чистая прибыль | 12000 | 13000 | 1000 | 8,3% |
Из этого примера факторного анализа можно сделать несколько выводов:
- Себестоимость единицы продукции увеличилась на 3,1%, что явилось негативным фактором.
- Однако доход все равно увеличился на 14,3%.
- Также увеличилась и чистая прибыль на 8,3%.
Поэтому подобный рост себестоимости оказался приемлемым. Следовательно, действуют другие факторы, которые позволяют расти прибыли компании. Уточнить их степень влияния можно с помощью аналогичных расчетов.
источник
Постановка задачи.
Каждое экономическое, общественное и физическое явление находится во взаимодействии с другими явлениями. При изучении связей рассматриваемых явлений выделяют независимые признаки 

Зависимости между признаками подразделяются на две категории – функциональные и корреляционные.
При функциональных связях каждому значению фактора соответствует вполне определенное значение результативного признака:
Примером функциональной связи служит закон Ома:
При корреляционной связи результативный признак 

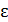
В экономических явлениях широко присутствуют корреляционные связи.
Так, на прибыльность банка влияют процентные ставки (факторный признак) и другие признаки – объемы операций, заработная плата сотрудников, затраты на оборудование и т.д. Влияние прочих факторов 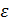

Методологию изучения статистической взаимосвязи рассмотрим на конкретном примере.
По семи областям проведено статистическое исследование по двум признакам: расходы на покупку продовольственных товаров в общих расходах и среднедневная заработная плата одного работающего. Каждый признак представлен выборкой из семи значений с целью уменьшения количества расчетов. Исследование выполнено случайным образом и его результаты отображены в таблице 1.1.
| № п/п | Среднедневная заработная плата одного работающего, тыс. руб., X | Расходы на покупку продовольственных товаров в общих расходах, %, Y |
| 45,1 | 68,8 | |
| 59,0 | 61,2 | |
| 57,2 | 59,9 | |
| 61,8 | 56,7 | |
| 58,8 | 55,0 | |
| 47,2 | 54,3 | |
| 55,2 | 49,3 |
Требуетсяпровести регрессионный и корреляционный анализ по двум выборкам для нахождения уравнения регрессии между двумя признаками. Уравнение регрессии позволит в дальнейшем формировать прогноз на будущее.
Выбор вида математической функции можно осуществить тремя методами: графическим, аналитическим и экспериментальным.
Построение графика зависимости результирующего признака от факторного .
Суть этапа заключается в построении зависимости результирующего признака 





Рисунок 1.1 – Корреляционное поле зависимости 
I – Линейная модель.
Цель этапа – установить уравнение связи двух переменных Y и X. Выберем простейшее линейное уравнение.
Линейное уравнение имеет вид y = a + bx. Для расчета коэффициентов а и b составим систему нормальных уравнений, полученных по методу наименьших квадратов-МНК:
По исходным данным задачи рассчитаем: 
| Таблица 1.2 | ||||||||
| Линейная модель | ||||||||
| №п/п |  |  | 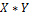 |  |  |  |  |  |
| 45,10 | 68,80 | 3102,88 | 2034,01 | 4733,44 | 61,10 | 7,71 | 11,20 | |
| 59,00 | 61,20 | 3610,80 | 3481,00 | 3745,44 | 56,23 | 4,97 | 8,12 | |
| 57,20 | 59,90 | 3426,28 | 3271,84 | 3588,01 | 56,86 | 3,04 | 5,08 | |
| 61,80 | 56,70 | 3504,06 | 3819,24 | 3214,89 | 55,25 | 1,45 | 2,56 | |
| 58,80 | 55,00 | 3234,00 | 3457,44 | 3025,00 | 56,30 | -1,30 | 2,36 | |
| 47,20 | 54,30 | 2562,96 | 2227,84 | 2948,49 | 60,36 | -6,06 | 11,16 | |
| 55,20 | 49,30 | 2721,36 | 3047,04 | 2430,49 | 57,56 | -8,26 | 16,75 | |
| Сумма | 384,30 | 405,20 | 22162,34 | 21338,41 | 23685,76 | 403,66 | 1,55 | 57,23 |
| Среднее значение | 54,90 | 57,89 | 3166,05 | 3048,34 | 3383,68 | — | — | 8,18 |
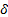 | 5,86 | 5,74 | — | — | — | — | — | — |
 | 34,33 | 32,92 | — | — | — | — | — | — |
Коэффициенты 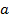

где, 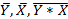

Уравнение линейной регрессии примет окончательный вид:
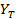
Теоретические значения 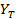

Экономический смысл коэффициента 
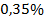
Найдем среднюю ошибку аппроксимации 
Для нашей задачи 
Допустимый предел 
Таким образом, средняя ошибка аппроксимации 
Цель этапа – рассчитать линейный коэффициент корреляции и установить силу связи между 

Линейный коэффициент корреляции найдем по формуле
где, 

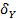

Значение 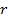
Определим коэффициент детерминации, который получим путем возведения коэффициента корреляции в квадрат.
Коэффициент детерминации также указывает на влияние фактора 

Вариация результата 


Оценка значимости уравнения регрессии.
Оценка значимости уравнения регрессии проводится с помощью F-критерия Фишера. Выдвигается гипотеза 


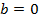
Процесс оценки нулевой гипотезы 
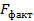

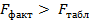



Уравнение регрессии значимо.
Если 



Для линейной модели 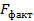
где 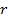
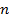

1. Определяем К1, которое равно количеству факторов 

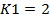
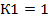
2. Определяем 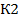
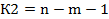
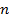

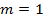
3. На пересечении столбца 



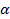

Следовательно, уравнение регрессии незначимо, ненадежно. Требуется подбор другого уравнения, например, одного из нелинейных.
II – Нелинейная модель
Предположим теперь, что результирующий фактор 



Выберем гиперболическую модель для уменьшения количества расчетов.
Уравнение равносторонней гиперболы
Для определение параметров 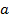

Чтобы определить параметры уравнения гиперболы, необходимо привести ее к линейному виду. Для этого сделаем замену переменной 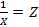
По исходным данным рассчитаем 
| таблица 1.3 | ||||||||||
| Нелинейная модель | ||||||||||
| №п/п |  |  |  |  | 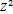 |  |  | 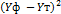 | 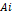 |  |
| 45,10 | 68,80 | 0,02 | 1,53 | 0,000492 | 4733,44 | 61,82 | 48,71 | 10,14 | 119,12 | |
| 59,00 | 61,20 | 0,02 | 1,04 | 0,000287 | 3745,44 | 56,31 | 23,90 | 7,99 | 10,98 | |
| 57,20 | 59,90 | 0,02 | 1,05 | 0,000306 | 3588,01 | 56,87 | 9,16 | 5,05 | 4,06 | |
| 61,80 | 56,70 | 0,02 | 0,92 | 0,000262 | 3214,89 | 55,50 | 1,44 | 2,11 | 1,41 | |
| 58,80 | 55,00 | 0,02 | 0,94 | 0,000289 | 3025,00 | 56,37 | 1,88 | 2,49 | 8,33 | |
| 47,20 | 54,30 | 0,02 | 1,15 | 0,000449 | 2948,49 | 60,78 | 41,99 | 11,93 | 12,86 | |
| 55,20 | 49,30 | 0,02 | 0,89 | 0,000328 | 2430,49 | 57,54 | 67,93 | 16,72 | 73,71 | |
| Сумма | 384,30 | 405,20 | 0,13 | 7,51 | 0,002413 | 23685,76 | 405,20 | 195,01 | 56,45 | 230,47 |
| Сред знач | 54,90 | 57,89 | 0,02 | 1,07 | 0,000345 | 3383,68 | 27,86 | 8,06 | 32,92 | |
| δ | 5,86 | 5,74 | 0,002134 | |||||||
| δ^2 | 34,33 | 32,92 | 0,000005 |
Примечание. Значения Z рассчитываем до 4-го знака после запятой.
Коэффициенты 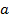

где,
Уравнение гиперболы примет вид:
Здесь 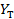

Качество гиперболической модели определяет средняя ошибка аппроксимации:
Качество построения модели оценивается как хорошее, если 
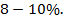
Сила связи между результативным признаком 

Связь между признаками 

Долю дисперсии, объясняемую регрессией, в общей дисперсии результативного признака 
Вариация результата 
Дата добавления: 2016-12-29 ; просмотров: 1101 | Нарушение авторских прав
источник
На днях приезжала моя теща и попросила помочь ей с построением достаточно замороченных диаграмм в Excel’е (для презентации). Опыт оказался интересным и которым я, собственно, хочу поделиться.
Итак, имеем два значения – одно плановое, второе проектное (или базовое и отчетное) и имеем значения отклонения факторов. Задача: построить в Excel красивую диаграмму отображения этих факторов.
Рис.0. Окончательный результат.
Создаем в Excel таблицу, в которой у нас находятся необходимые данные (см.рис.1).
После этого разносим их следующим образом (рис.2)
Теперь подпишем столбцы – столбец I – Значение, далее – Основа, далее Влияние фактора (рис.3).
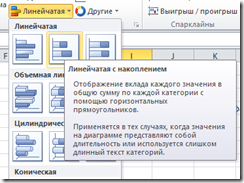
В качестве базовой диаграммы мы будем использовать либо гистограмму либо линейчатую с наполнением.
Рис.4. Используемые типы диаграмм
Теперь поясню на рис.5 что я имею в виду под основой – это такое значение некоторого ряда которое позволит построить нам диаграмму максимально точно.
В вычислении значений этого ряда поступаем следующим образом:
1. Значение первой основы (сразу после базового значения) принимаем равным либо базовому значению (если первый фактор имеет позитивное влияние) либо (базовое значение – величина влияния) – если фактор имеет негативное влияние.
2. Для последующих основ применяется та же схема. Если значение фактора положительное, то за основу берем результирующее значение, полученное на предыдущем факторе. Если же отрицательное, то берем (результирующее – абсолютное значение негативного фактора).
Что такое основа легко понять по рис.5.
Ту величину, которую я назвал “Влияние фактора” вычисляем как значение изменения фактора по модулю (абсолютное значение) с помощью функции ABS() – рис.6.
Рис.6. Вычисленные значения “Влияния фактора”
Далее по описанному выше алгоритму рассчитываем значения основы для каждого фактора.
Для первой основы используются следующая функция:
=ЕСЛИ(L6>0;I5;I5+L6) — т.е. если первый фактор больше нуля, то берем базовое значение, в противном случае берем базовое + значение изменения фактора (в нашем примере получается просто 100).
=ЕСЛИ(L7>0;M6;M6+L7) — т.е. если фактор больше нуля, то берем полученное на предыдущем факторе результирующее значение, в противном случае берем базовое + значение изменения фактора.
Ахтунг! Не забывайте про правила сложения – если я говорю “плюс значение”, это значит, что подразумевается не абсолютное значение, а позитивное или негативное. Т.е. для третьего фактора получим следующую логику:
Значение изменения фактора меньше нуля, следовательно берем сумму предыдущего результирующего значения и значения изменения фактора, т.е. основа будет равна 170+(-30)=170-30=140.
Результирующее значение вычисляется по формуле:
=ЕСЛИ(L6>0;J6+L6;J6) – т.е. если изменения фактора позитивное, то результирующим значением будет сумма предыдущего результирующего значения и величины изменения фактора, а в противном случае – просто значение основы. Далее переходим уже непосредственно к построению диаграммы. Выделяем ячейки от названия категорий до столбца “Влияние фактора” включительно.
И вставляем необходимый тип диаграммы (в данном случае – гистограмму).
Рис.8. Полученный результат
Дальше наводим красоту – переносим на новый лист диаграмму и заодно поправляем мою ошибку в выборе исходных данных (Отчетное значение принимаем 160, а не 150).
Удаляем вертикальную ось, удаляем основные вертикальные и горизонтальные линии осей и у нас получается нечто вроде рис.9.
Дальше в свойствах ряда изменяем боковой зазор до 10% и ряду “Основа” выставляем отсутствие заливки и линий – т.е. делаем его невидимым.
В свойствах горизонтальной оси также поставим “Нет линий” (рис.10).
Рис.10. Делаем ось невидимой
Далее добавляем рядам “Влияние фактора” и “Значение” подписи данных. Но получается маленькая нестыковка – даже в тех случаях, когда изменение фактора было отрицательным у нас выводятся положительные значения. Для этого дальше переходим обратно на лист 1 и выставляем соответственные форматы для позитивных и негативных значений.
Для негативных, соответственно: –0,0 – рис.11
Рис.11. Изменение формата чисел в столбце “Влияние фактора”.
Получившийся результат показан на рис.12
Рис.12. Подписи данных после изменения формата
Как видим, уже все изменения отображаются логически верно. Остался маленький штришок – находим точки ряда с негативным изменением и изменяем им цвет заливки на красный, а также меняем цвета подписей данных для этого ряда для большей наглядности (рис.13).
Рис.13. Окончательный результат.
Мы получили симпатичную диаграммку, которую не стыдно вставить в презентацию или в документ.
источник
Факторный анализ покажет, как повлияли на прибыль изменившиеся цена, себестоимость и объем продаж. С его помощью можно быстро выяснить количественную связь между закупкой нового оборудования и производительностью труда. И это только два примера. А в нашей статье их – семь. Да еще Excel-модель, готовая сама все рассчитать.
Методика факторного анализа кратко – это способ измерить влияние причин на результат или следствие.
Для иллюстрации возьмем самые простые зависимости:
- Цена товара, количество продаж и выручка. Где здесь следствие, а где причины? Очевидно, что цена и количество напрямую влияют на выручку. Значит, это факторы, а выручка – результирующий показатель;
- Себестоимость производства и затраты по элементам. Так как себестоимость складывается из материальных затрат, оплаты труда, отчислений с нее, амортизации и прочих составляющих, то это – причины. Сама же себестоимость – следствие;
- Производительность труда, обеспеченность рабочих основными средствами (фондовооруженность) и эффективность работы оборудования (фондоотдача). Этот пример – посложнее, ведь многое зависит от цели, стоящей перед аналитиком. Но один из наиболее расхожих вариантов такой: фондовооруженность и фондоотдача – факторы, а производительность труда – результат.
Овладеть методикой факторного анализа означает научиться, во-первых, формировать модели (формулы), а во-вторых, количественно измерять влияние факторов на исследуемый показатель.
Решение от «Финансового директора» позволит проанализировать расхождения факта с планом и выяснить, почему они возникли и какие факторы повлияли.
- Определитесь с тем, какой именно показатель нуждается в углубленном анализе. Он и будет тем самым следствием (результатом), для которого потребуется количественно измерить причины.
- Решите, какая факторная модель будет использоваться. Факторная модель – это формульная зависимость между причинами и результатом. Устанавливается она просто. Достаточно вспомнить порядок расчета результирующего показателя или поискать уже готовые варианты, если требуется подход посерьезнее. В приведенных в начале статьи примерах модели будут такими:
- Выручка = Цена × Количество;
- Себестоимость производства = Материальные затраты + Затраты на оплату труда + Социальные отчисления + Амортизация + Прочие затраты;
- Производительность труда = Фондовооруженность × Фондоотдача.
- Оценитевлияние факторов на результат. В этом помогут сразу несколько способов. Наиболее популярные из них – методы цепных подстановок и абсолютных разниц.
- Проанализируйте полученные цифры. В ходе анализа постарайтесь найти ответы на вопросы: какие факторы оказали отрицательное воздействие на результирующий показатель? влияние каких практически незаметно? что нужно сделать, чтобы ослабить отрицательную роль первых и усилить положительный эффект от вторых? Заметим, что ответ на последний вопрос лежит в плоскости управленческих решений, так как может потребовать пересмотра ценовой политики, подходов к мотивации сотрудников, инвестиционных решений предприятия и т.п.
Нужны готовые решения? Семь факторных моделей и расчет по ним уже ждут вас в нашей Excel-модели. Скачайте, чтобы углубленно проанализировать прибыль от продаж, себестоимость производства и производительность труда.
Для того, чтобы грамотно проводить факторный анализ на практике, нужно еще немного теоретических знаний. Например, о том, какие в нем есть два принципиально разнящихся подхода и какими по виду бывают факторные модели.
Первый момент – о подходах – поможет не ошибиться с подбором факторов в модель. Ведь, по сути, для каждого следствия есть множество причин. Допустим, на производительность труда метеозависимых людей влияют в том числе и геомагнитные бури. Но как формализовать это влияние, превратив его в строгую математическую формулу? Вообще можно, но сложно. А порой и не нужно.
Второй – о типах моделей – это основа для правильного выбора способов оценки влияния факторов. Например, тот же метод абсолютных разниц применим не для каждой факторной модели.
Все, что важно знать про методику факторного анализа, мы представили на схеме и описали ниже.

Есть несколько классификаций. В этой статье рассмотрим одну, но, пожалуй, самую важную для специалиста-практика.
С позиции жесткости или однозначно выраженной определенности связи между следствием и причинами факторный анализ бывает:
Детерминированный – это когда зависимость между результатом и факторами выражается строго заданной математической формулой, и она будет работать в любых условиях. Например, если поднять цену на товар в два раза и при этом добиться, чтобы количество продаж осталось прежним, то выручка вырастет также ровно в два раза.
Стохастический – в этом случае связь между результатом и факторами, несомненно, есть, но вот выразить ее без проведения дополнительных вычислений – невозможно.
Здесь снова обратимся к примеру зависимости между производительностью труда отдельных работников и геомагнитными возмущениями. Да, влияние определенно есть. Но какое оно? Как его измерить? Можно ли сказать, что если геомагнитная активность вырастет на 1 балл, то производительность труда снизится на 10%? Очевидно, что нет. Конечно, можно собрать сведения о самочувствии людей за некоторый промежуток времени и на этой основе построить корреляционно-регрессионную зависимость. Но формула, которую получат для жителей Владивостока, возможно, совсем не будет работать для москвичей и наоборот.
Как провести факторный анализ ключевых финансовых показателей
Смотрите, как узнать, почему выручка, себестоимость, EBITDA за полугодие отличаются от запланированных значений. Готовые Excel-модели для шести ключевых показателей и примеры расчетов – в этом решении.
Вот их краткая характеристика с примерами.
Связь между результатом и факторами: через алгебраическую сумму. Алгебраическая в данном случае означает, что факторы объединяются в формуле не только через сложение, но и через вычитание.
- Совокупные затраты предприятия = Переменные затраты + Постоянные затраты;
- Маржинальный доход на единицу товара = Цена продажи – Цена приобретения – Прочие переменные затраты на единицу;
- Прибыль (убыток) от продаж = Выручка-нетто – Себестоимость продаж – Коммерческие расходы – Управленческие расходы;
- Собственные оборотные средства = Собственный капитал – Внеоборотные активы.
Связь между результатом и факторами: через произведение.
- Объем производства продукции за год = Средняя численность работников × Среднегодовая выработка продукции одним работников;
- Среднегодовая выработка продукции одним работником = Среднее количество дней, отработанных одним работником за год × Средняя продолжительность рабочей смены × Среднечасовая выработка продукции одним работником;
- Рентабельность активов = Рентабельность продаж × Коэффициент оборачиваемости активов.
Связь между результатом и факторами: через деление.
- Рентабельность продаж = Чистая прибыль ÷ Выручка;
- Рентабельность продаж = Рентабельность собственного капитала ÷ Коэффициент оборачиваемости активов ÷ Мультипликатор собственного капитала;
- Финансовый леверидж = Заемный капитал ÷ Собственный капитал.
Связь между результатом и факторами: одновременно используются алгебраическая сумма, произведение и деление.
Некоторые обобщенные варианты формул:
- Y = (Х1 + Х2) ÷ Х3;
- Y = (Х1 – Х2) × Х3;
- Y = Х1 × Х2 + Х3 × Х4;
- Y = Х1 ÷ Х2 + Х3 ÷ Х4 и т.д.
- Точка безубыточности = Постоянные затраты ÷ (Цена за единицу товара – Переменные затраты на единицу товара);
- Маржа безопасности = (Плановый/фактический объем продаж – Объем продаж в точке безубыточности) ÷ Плановый/фактический объем продаж;
- Коэффициент обеспеченности запасов собственными источниками = (Собственный капитал – Внеоборотные активы) ÷ Запасы.
Таких способов – несколько, а именно:
- цепных подстановок;
- абсолютных разниц;
- относительных разниц;
- интегральный метод;
- логарифмический метод.
Чтобы успешно решать задачи факторного анализа, достаточно знать, как реализуются первые два подхода и в чем их ограничения. Поэтому сосредоточимся именно на них.
В чем суть: рассчитываются несколько условных значений результирующего признака и в строго определенном порядке сравниваются между собой, а также со значениями результата в базовом и отчетном периодах. Сразу оговорим терминологию:
- базовый период – это любой предыдущий, например, за прошлый год, квартал, месяц или на предыдущую отчетную дату;
- отчетный период – самый последний по времени из анализируемых. Базовый и отчетный периоды должны соответствовать друг другу по продолжительности. Допустим, все они – это только годы или только кварталы;
- условное значение результирующего признака – величина, которая в реальности никогда не достигалась. Отсюда и название – «условное». Оно необходимо только для расчетных целей.
- Рассчитайте первое условное значение результата. Для этого в формуле факторной модели, где все значения взяты из базового периода, величину первого фактора замените на отчетную.
- Найдите разницу между первым условным значением результата и его же величиной в базовом периоде. Она покажет влияние первого исследуемого фактора.
- Вычислите второе условное значение результата. Чтобы это сделать, в формулу факторной модели введите отчетную величину для второго исследуемого фактора. Помните, что так как первый фактор уже однажды изменил значение с базового на отчетное, то для него откат назад не делается. Во всех следующих расчетах он будет браться с отчетной величиной. Это применимо и ко всем остальным факторам, значения которых изменялись с базового на отчетное;
- Найдите разницу между вторым и первым условными значениями результата. Это будет влияние второго фактора на результирующий показатель;
- Повторите процесс для всех факторов в модели. На последнем шаге расчета разница определяется между отчетным значением результата и последним условным значением.
- Количество условных значений всегда на единицу меньше количества факторов. То есть если модель двухфакторная, то условное значение будет одно, а из числа приведенных выше этапов надо сделать только I, II и V;
- Самое главное – не перепутать что из чего вычитать. Общее правило такое: из последнего звена цепочки расчета вычитается предыдущее. Из первого условного – базовое, из второго условного – первое условное, из отчетного – последнее условное;
- Величина влияния зависит от места фактора в модели. Если переставить факторы местами и провести расчет заново, то получатся немного другие значения. Причина – воздействие неразложимого остатка или взаимного влияния факторов друг на друга. Методы цепных подстановок, абсолютных и относительных разниц не решают данную проблему. Поэтому если требуются высокая точность вычисления и меньшее искажение из-за неразложимого остатка, то применяйте более сложные интегральный и логарифмический способы;
- Суммарное влияние всех факторов равняется разнице между отчетными и базовыми значениями результата. Это так вообще для всех способов оценки влияния факторов;
- Метод цепных подстановок – единственный универсальный в факторном анализе, который подойдет для моделей любого типа.
Как реализовать на примере:
- Возьмем факторную модель [Точка безубыточности = Постоянные затраты ÷ (Цена за единицу товара – Переменные затраты на единицу товара)]. Для простоты запишем ее через условные обозначения, причем со значениями из базового периода. Получим: ТБ = ПостЗ ÷ (Цед. 0 – ПерЗед. 0);
- Первое условное значение для точки безубыточности рассчитаем по формуле: ТБусл. 1 = ПостЗ1 ÷ (Цед. 0 – ПерЗед. 0);
- Влияние первого фактора – постоянных затрат – вычислим так: ∆ТБ(ПостЗ) = ТБусл.1 – ТБ;
- Теперь рассчитаем второе условное значение для ТБ: ТБусл. 2 = ПостЗ1 ÷ (Цед. 1 – ПерЗед. 0). Обратите внимание, что величина постоянных затрат не меняется обратно на значение базового периода;
- Вычисляем влияние второго фактора – цены за единицу: ∆ТБ(Цед.) = ТБусл. 2 – ТБусл. 1;
- Если теперь в формуле взять переменные затраты со значением из отчетного периода, то на выходе получим не еще одно условное, а фактическое значение результата: ТБ1 = ПостЗ1 ÷ (Цед. 1 – ПерЗед. 1);
- На последнем шаге считаем влияние третьего фактора – переменных затрат на единицу товара: ∆ТБ(ПерЗед.) = ТБ1 – ТБусл. 2;
- Если расчеты сделаны верно, то должно выполняться равенство ∆ТБ = ∆ТБ(ПостЗ) + ∆ТБ(Цед.) + ∆ТБ(ПерЗед.).
В чем суть: для расчета влияния фактора нужно найти его абсолютное отклонение (разницу) между данными отчетного и базового периода.
- Вычислите влияние первого фактора. Для этого подставьте в формулу его абсолютное отклонение. Все остальные факторы в модели берите со значениями из базового периода.
- Рассчитайте воздействие второго фактора. С этой целью в формулу опять подставляется его абсолютное отклонение. Как быть с прочими показателями? Все, которые находятся левее анализируемого фактора, берутся с отчетными значениями. Все, которые правее, – с базовыми.
- Повторите процесс для всех факторов в модели, используя схему: анализируемый фактор берется со значком ∆, стоящие от него слева в формуле – со значком 1, а справа – с 0.
Что важно знать: простота реализации метода сочетается с ограниченностью применения. Он используется только для мультипликативных и смешанных моделей мультипликативно-аддитивного типа.
Как реализовать на примере:
- Воспользуемся факторной моделью [Среднегодовая выработка продукции одним работником = Среднее количество дней, отработанных одним работником за год × Средняя продолжительность рабочей смены × Среднечасовая выработка продукции одним работником]. Через условные обозначения она будет такой: ГВ = Д × П × ЧВ.
- Влияние количества дней рассчитаем как произведение их абсолютной разницы и двух других факторов в модели со значениями из базового периода: ∆ГВ(Д) = ∆Д × П × ЧВ0.
- Влияние продолжительности рабочей смены вычисляем по аналогичной схеме. При этом помним, что величину Д следует брать уже из отчетного периода: ∆ГВ(П) = Д1 × ∆П × ЧВ0.
- Теперь остается вычислить влияние часовой выработки. Факторы слева от нее будут с индексом 1: ∆ГВ(ЧВ) = Д1 × П1 × ∆ЧВ.
- Проверяем выполнение равенства: ∆ГВ = ∆ГВ(Д) + ∆ГВ(П) + ∆ГВ(ЧВ).
Давайте посмотрим, как на практике применяются три факторные модели для анализа прибыли от продаж, себестоимости производства и производительности труда. Все используемые формулы объединяет возможность выполнить расчет исключительно по данным финансовой отчетности и годового отчета. Воспользуемся информацией ПАО «Новолипецкий металлургический комбинат» (ПАО «НЛМК»).
За основу возьмем аддитивную факторную модель: Прибыль (убыток) от продаж = Выручка – Себестоимость продаж – Коммерческие расходы – Управленческие расходы.
Через условные обозначения запишем ее так: ПП = В – СП – КР – УР.
В таблице приведены исходные данные, а также сделан расчет влияния факторов.
Таблица 1 – Факторный анализ прибыли от продаж для ПАО «НЛМК»
1.1 выручка (строка 2210 отчета о финансовых результатах – ОФР)
1.2 себестоимость продаж (2120 ОФР)
1.3 коммерческие расходы (2210 ОФР)
1.4 управленческие расходы (2220 ОФР)
1.5 прибыль от продаж (2200 ОФР)
2 Расчет влияния факторов на прибыль от продаж, млн р.
2.1 первое условное значение прибыли от продаж ППусл. 1
(В1 – СП – КР – УР)
2.2 влияние выручки ∆ПП(В) (ППусл. 1 – ПП)
2.4 влияние себестоимости продаж ∆ПП(СП) (ППусл. 2 – ППусл. 1)
2.6 влияние коммерческих расходов ∆ПП(КР) (ППусл. 3 – ППусл. 2)
2.7 влияние управленческих расходов ∆ПП(УР) (ПП1 – ППусл. 3)
3 Общее влияние факторов (2.2 + 2.4 + 2.6 + 2.7)
Вывод: положительное влияние выручки более, чем в два раза перекрыло отрицательное воздействие расходов по обычным видам деятельности. С этой точки зрения деятельность ПАО «НЛМК» очень эффективна и характеризуется интенсивным подходом к развитию.
Расчет будем вести по формуле: Себестоимость производства единицы продукции = Материалоемкость + Зарплатоемкость + Амортизациеемкость + Накладоемкость.
Иначе: СПЕ = МЕ + ЗЕ + АЕ + НЕ.
Примечание. Эту факторную модель легко получить, если знать соотношения:
- Себестоимость производства единицы продукции = Совокупные затраты ÷ Объем произведенной продукции;
- Совокупные затраты = Материальные затраты + Затраты на оплату труда и социальные отчисления + Амортизация + Прочие накладные затраты;
- Материалоемкость = Материальные затраты ÷ Объем произведенной продукции;
- Зарплатоемкость = Затраты на оплату труда и социальные отчисления ÷ Объем произведенной продукции;
- Амортизациеемкость = Амортизация ÷ Объем произведенной продукции;
- Накладоемкость = Прочие накладные затраты ÷ Объем произведенной продукции.
Таблица 2 – Факторный анализ себестоимости производства единицы продукции для ПАО «НЛМК»
1.1 материальные затраты, млн р. (строка 5610 пояснений к бухгалтерскому балансу и отчету о финансовых результатах – пояснения к ББ и ОФР)
1.2 затраты на оплату труда и отчисления на социальные нужды, млн р. (5620 + 5630 пояснений к ББ и ОФР)
1.3 амортизация, млн р. (5640 пояснений к ББ и ОФР)
1.4 прочие затраты, млн р. (5650 пояснений к ББ и ОФР)
1.5 объем производства, млн т (годовой отчет)
2 Результирующий и факторные показатели модели, р./т:
источник