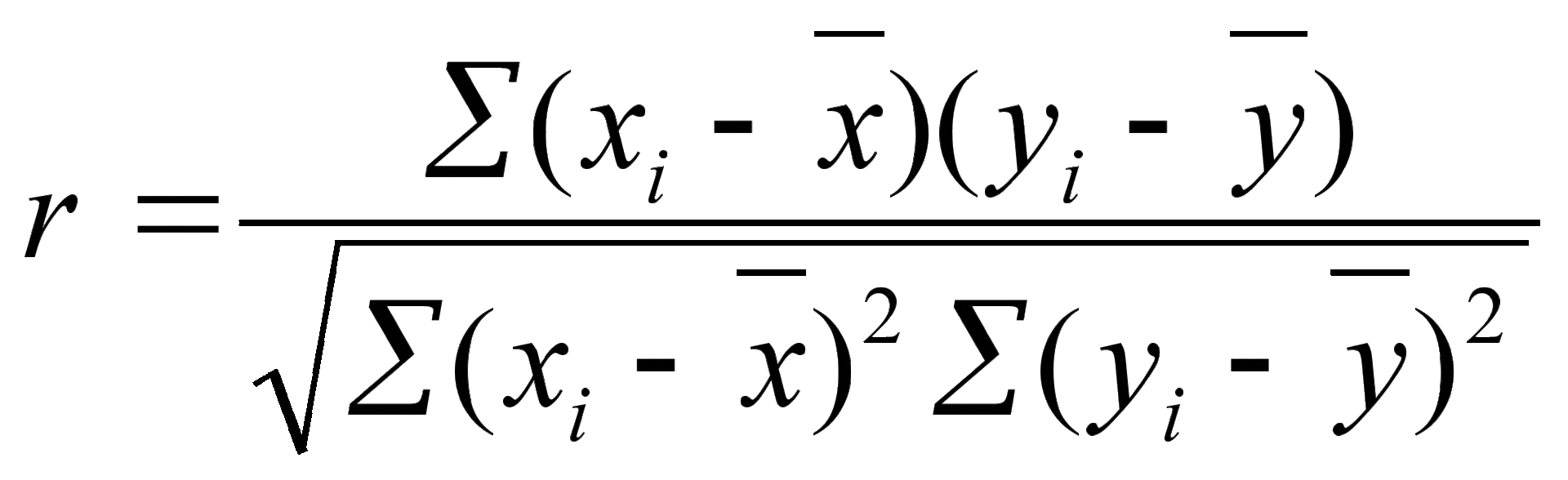Как начать анализ статистических данных

Достаточно часто возникают явления, которые можно проанализировать исключительно при помощи статистических методов. В этой связи для каждого субъекта, стремящегося глубоко изучить проблему, проникнуть в суть темы, важно иметь представление о них. В статье разберемся, что такое статистический анализ данных, каковы его особенности, а также какие методы применяют при его проведении.

Статистику рассматривают в качестве специфичной науки, системы госорганов, а также как набор цифр. Между тем далеко не все цифры можно считать статистикой. Разберемся в этом вопросе.

Для начала следует вспомнить, что слово «статистика» имеет латинские корни и происходит от понятия status. В буквальном переводе термин означает «определенное положение предметов, вещей». Следовательно, статистическими признаются только такие данные, с помощью которых фиксируются относительно устойчивые явления. Анализ, собственно, и выявляет эту устойчивость. Его используют, к примеру, при изучении социально-экономических, политических явлений.

Применение статистического анализа позволяет отображать количественные показатели в неразрывной связи с качественными. В результате исследователь может увидеть взаимодействие фактов, установить закономерности, выявить типичные признаки ситуаций, сценарии развития, обосновать прогноз.

Статистический анализ – это один из ключевых инструментов СМИ. Чаще всего его используют в деловых изданиях, таких как, например, «Ведомости», «Коммерсант», «Эксперт-профи» и пр. В них всегда публикуются «аналитические рассуждения» о валютном курсе, котировке акций, учетных ставках, инвестициях, рынке, экономике в целом.

Разумеется, чтобы результаты анализа были достоверными, постоянно проводится сбор данных.

Сбор данных может осуществляться по-разному. Главное, чтобы способы не нарушали закон и не ущемляли интересы других лиц. Если говорить о СМИ, то для них ключевыми источниками информации выступают государственные статистические органы. Эти структуры должны:

Собирать отчетные сведения в соответствии с утвержденными программами.
Группировать информацию по тем или иным критериям, наиболее значимым для исследуемого явления, формировать сводки.
Проводить собственный статистический анализ.

В задачи уполномоченных госорганов входит также предоставление полученных ими данных в отчетах, тематических подборках или пресс-релизах. В последнее время статистика публикуется на официальных сайтах госструктур.

Кроме указанных органов, информацию можно получить в Едином госреестре предприятий, учреждений, объединений и организаций. Цель его создания состоит в формировании единой информационной базы.

Для проведения анализа можно использовать информацию, полученную от межправительственных организаций. Существуют специальные базы данных экономической статистики стран.

Часто информация поступает от частных лиц, общественных организаций. Эти субъекты обычно ведут свою статистику. Так, к примеру, Союз охраны птиц в России регулярно устраивает так называемые соловьиные вечера. В конце мая через СМИ организация приглашает всех желающих поучаствовать в подсчете соловьев на территории Москвы. Полученные сведения обрабатываются группой экспертов. После этого сведения переносятся в специальную карту.

Многие журналисты обращаются за информацией к представителям других авторитетных СМИ, пользующихся у аудитории популярностью. Распространенным способом получения данных является опрос. При этом опрашиваемыми могут стать как рядовые граждане, так и эксперты в какой-либо области.

Перечень показателей, необходимых для проведения анализа, зависит от специфики исследуемого явления. К примеру, если изучается уровень благосостояния населения, приоритетными считаются данные о качестве жизни граждан, прожиточном минимуме на данной территории, размере МРОТ, пенсии, стипендии, потребительской корзины. При исследовании демографической ситуации важны показатели смертности и рождаемости, число мигрантов. Если изучается сфера промышленного производства, важные сведения для статистического анализа – это количество предприятий, их виды, объем продукции, уровень производительности труда и т. д.

Как правило, при описании тех или иных явлений используются средние арифметические величины. Для их получения числа складывают друг с другом, а полученный результат делят на их количество.

Средние величины используются в качестве обобщающих показателей. Однако они не позволяют описать конкретные моменты. К примеру, в ходе анализа установлено, что средняя зарплата по России составляет 30 тыс. р. Этот показатель не говорит о том, что все работающие граждане страны получают именно эту сумму. Более того, у кого-то зарплата может быть и выше, а у кого-то – ниже этой цифры.

Их находят в результате сравнительного анализа. В статистике, кроме средних, используются абсолютные величины. При их сопоставлении как раз и определяются относительные показатели.

Например, установлено, что в один госорган приходит 5 тысяч писем ежемесячно, а в другой – 1 000. Выходит, что первая структура получает в 5 раз больше обращений. При сравнении средних показателей относительная величина может быть выражена в процентах. К примеру, средний заработок фармацевта составляет 70 % от ср. з/п инженера.

Они представляют собой систематизацию признаков исследуемого события для выявления динамики его развития. К примеру, установлено, что в 1997 г. речной транспорт всех ведомств и управлений перевез 52,4 млн тонн груза, а в 2007 г. – 101,2 млн т. Чтобы понять изменения характера транспортировок за период с 1997 по 2007 г., можно сгруппировать итоговые показатели по видам объектов, а затем сравнить группы друг с другом. В итоге можно получить более полные сведения о развитии грузооборота.

Их достаточно широко применяют при исследовании динамики событий. Индекс в статистическом анализе – это средний показатель, отражающий изменение явления под воздействием другого события, абсолютные показатели которого признаны неизменными.

К примеру, в демографии в качестве специфического индекса может выступать величина естественной убыли (прироста) населения. Ее определяют при сравнении уровня рождаемости и смертности.

Они используются для отображения динамики развития события. Для этого применяют фигуры, точки, линии, имеющие условные значения. Графики, с помощью которых выражаются количественные соотношения, именуются диаграммами или динамическими кривыми. Благодаря им можно наглядно увидеть динамику развития какого-то явления.

График, показывающий увеличение количества лиц, страдающих остеохондрозом, представляет собой кривую, уходящую вверх. Соответственно, по ней можно наглядно увидеть тенденцию заболеваемости. Люди, даже не прочитав текстовый материал, могут сформулировать выводы о сложившейся динамике и спрогнозировать развитие ситуации в дальнейшем.

Они очень часто используются для отражения данных. С помощью статистических таблиц можно сопоставлять информацию по изменяющимся со временем показателям, различающимся в зависимости от страны и пр. Они представляют собой наглядную статистику, которой зачастую не нужны комментарии.

В основе статистического анализа лежат приемы и способы сбора, обработки и обобщения сведений. В зависимости от природы методы могут быть количественными и категориальными.

При помощи первых получают метрические данные, которые по своей структуре являются непрерывными. Их можно измерить при помощи интервальной шкалы. Она представляет собой систему чисел, равные промежутки между которыми отражают периодичность значений изучаемых показателей. Также используется шкала отношений. В ней, кроме расстояния, определяется также порядок значений.

Неметрические (категориальные) данные представляют собой качественные сведения, количество уникальных категорий и значений которых ограничено. Они могут быть представлены в виде номинальных или порядковых показателей. Первые используют для нумерации объектов. Для вторых предусматривается естественный порядок.

Они применяются в том случае, если для оценки всех элементов выборки используется единый измеритель или если последних несколько для каждого компонента, но переменные исследуются обособленно друг от друга.

Одномерные методы различаются в зависимости от типа данных: метрические или неметрические. Первые измеряют по относительной или интервальной шкале, вторые – по номинальной или порядковой. Кроме этого, деление методов осуществляется на классы в зависимости от количества исследуемых выборок. При этом необходимо учитывать, что это число определяют по тому, как осуществляется работа с информацией для конкретного анализа, а не по способу сбора данных.

Цель статистического анализа может состоять в изучении воздействия одного либо нескольких факторов на конкретный признак объекта. Однофакторный дисперсионный метод применяется тогда, когда у исследователя есть 3 и больше независимые выборки. При этом они должны быть получены из генеральной совокупности посредством изменения независимого фактора, для которого отсутствуют количественные измерения по каким-то причинам. Предполагается, что имеются различные и одинаковые выборочные дисперсии. В этой связи следует определить, оказал ли данный фактор значительное влияние на разброс или он стал следствием случайностей, возникших вследствие небольших объемов выборок.

Он представляет собой упорядоченное распределение единиц генеральной совокупности, как правило, по возрастающим (в редких случаях по убывающим) показателям признака и подсчет их числа с тем или другим значением признака.

Вариация является различием в показателе какого-либо признака у различных единиц конкретной совокупности, возникающим в один и тот же момент либо период. К примеру, сотрудники компании отличаются друг от друга по возрасту, росту, доходам, весу и пр. Возникает вариация вследствие того, что индивидуальные показатели признака формируются под комплексным влиянием разных факторов. В каждом конкретном случае они сочетаются по-разному.

Ранжированным. Он представлен в виде перечня отдельных единиц генеральной совокупности, расположенных в порядке убывания либо возрастания исследуемого признака.
Дискретным. Он представлен в форме таблицы, включающей в себя конкретные показатели изменяющегося признака х и количества единиц совокупности с заданной величиной f признака частот.
Интервальным. В этом случае показатель непрерывного признака задается с помощью интервалов. Они характеризуются частотой t.

Он проводится, если для оценки элементов выборки применяется 2 и более измерителя, и переменные изучаются одновременно. Такая форма статистического анализа отличается от одномерного способа в первую очередь тем, что при ее использовании внимание сосредотачивается на уровне взаимосвязи между явлениями, а не на средних показателях и распределениях (дисперсиях).

Среди основных методов многомерного статистического исследования выделяют:

Кросс-табуляцию. С ее использованием одновременно характеризуют значение двух и более переменных.
Дисперсионный статистический анализ. Этот метод ориентирован на поиск зависимостей среди экспериментальных данных посредством изучения существенности различий в средних показателях.
Ковариационный анализ. Он тесно связан с дисперсионным методом. При ковариационном исследовании зависимая переменная корректируется в соответствии с информацией, связанной с ней. Это обеспечивает возможность устранения изменчивости, вносимой извне, и, соответственно, повысить эффективность исследования.

Также существует дискриминантный анализ. Он применяется, если зависимая переменная является категориальной, а независимые (предикторы) – интервальными.

источник

Понятие «статистический анализ» традиционно ассоциируется с исключительно количественными, цифровыми показателями. Слово «статистика» имеет латинское происхождение и означает «состояние, положение вещей с точки зрения закона». Наполеон Бонапарт называл статистику «бюджетом вещей». В современном понимании, этот термин может быть использован в следующих значениях:

ü как специализированная отрасль знания по вопросам сбора и анализа данных. Термин «статистика» в этом значении стало применяться с середины XVIII века в Германии.

ü как массив определенных статистических данных (статистика рождаемости, статистика посещений сайта и т.п.).

ü как измеримая функция наблюдения в математической статистике: , где — выборка.

Принято считать, что статистика, как научное направление, появилось во второй половине XVIII – начале XIX веков. Конечно, методы и процедуры статистического учета применялись и развивались задолго до XVIII века. Действительно, еще в Древнем Китае проводились переписи населения, в Древнем Риме велся учет имущества граждан, да и в других царствах-государствах было что посчитать и записать. Ценность статистических методов, прежде всего в предоставлении фактов в наиболее сжатой форме. Статистика за сотни лет своей эволюции, отдельными элементами или комплексными методиками применялась и применяется и для административного, в том числе социально-политического управления, и для ведения деятельности отдельного предприятия.

Сейчас, в современном мире статистические методы применяются практически во всех сферах деятельности человека и являются методами сбора, классификации данных с последующим их анализом с целью выявления закономерностей.

Методы статистического анализа ориентированы на решения реальных задач, поэтому постоянно появляются и развиваются новые методы. Динамизм развития статистической науки и использование в самых различных областях деятельности человека, затрудняют классификацию статистических методов. Большинство исследователей с легкостью подразделяют эти методы по способу их применения и использования. В соответствии с этим подходом, статистика, как наука в современном мире, по степени охвата исследуемой области и глубины анализа подразделяется на следующие виды:

· теоретическая статистика (общая теория статистики) – разработка и исследование методов общего характера;

· прикладная статистика – разработка методов и моделей получения анализа статистических данных конкретных явлений и процессов в различных областях деятельности. Подразделяется на ряд подразделов, например, такие хорошо разработанные направления статистики, как математическую и экономическую статистику.

· статистический анализ конкретных данных. Например, медицинская статистика, правовая статистика, биометрика (измерение каких-либо параметров тела человека), технометрика (измерение технических параметров приборов и оборудования), наукометрика (статистические параметры состояния и развития различных направлений сферы образования и науки) и т.д.

Методы статистического анализа могут быть классифицированы по объему анализируемых данных и глубине их взаимосвязи и взаимозависимости. Данная классификация приведена на рисунке 8.2.1 «Классификация методов статистического анализа».

Статистические методы анализа

Одновариантные методы анализа Оценивается только одна характеристика, показатель или каждый показатель обособлено от всех других.

Многовариантные методы анализа Анализ проводится по двум и более показателям.

Методы анализа, использующие метрические показатели Используются данные, которые могут быть измерены по интервальной или относительной шкале

Методы анализа, использующие неметрические показатели Используются данные, которые могут быть измерены по номинальной или порядковой шкале

Методы анализа зависимых переменных Используются для определения одновременных взаимосвязей между двумя или больше явлениями. Этот такие методы анализа, как построение таблиц сопряженности признаков (кросс-табуляция), регрессионный анализ, совместный анализ и т.п.

Методы анализа взаимозависимых переменныхИспользуются для анализа данных всех возможных в том числе скрытых взаимосвязей – взаимозависимости (например, факторный анализ) и межобъектного сходства (например, методы кластерного анализа, многомерного шкалирования).

Рисунок 8.2.1 Классификация методов статистического анализа

Не нашли то, что искали? Воспользуйтесь поиском:

источник

Анализ данных и статистика — вещи одного порядка. Если статистика первооснова и источник информации, то анализ данных — это инструмент для ее исследования, и зачастую анализ данных без статистики невозможен.

Статистика — это изучение любых явлений в числовой форме. Статистика используется анализом данных в количественных исследованиях. Противоположность им — качественные, описывающие ситуацию без применения цифр, в текстовом выражении.

Количественный анализ статистических данных проводится по интервальной шкале и по рациональной:

интервальная шкала указывает, насколько тот или иной показатель больше или меньше другого и дает возможность подобрать похожие по свойствам соотношения показатели,
рациональная шкала показывает, во сколько раз тот или иной показатель больше или меньше другого, но в ней содержатся только положительные значения, что не всегда будет отражать реальное положение дел.

В анализе статистических данных можно выделить аналитический этап и описательный. Описательный этап — последний, он включает представление собранных данных в удобном графическом виде – в графиках, диаграммах, дашбордах. Аналитический этап — это анализ, заключающийся в использовании одного из следующих методов:

статистического наблюдения – систематического сбора данных по интересующим характеристикам;
сводки данных, в которой можно обработать информацию после наблюдения; она описывает отдельные факты как часть общей совокупности или создает группировки, делит информацию по группам на основании каких-либо признаков;
определении абсолютной и относительной статистической величины; абсолютная величина придает данным количественные характеристики в индивидуальном порядке, в независимости от других данных; относительные величины описывают одни объекты или признаки относительно других;
метода выборки – использовании при анализе не всех данных, а только их части, отобранной по определенным правилам (выборка может быть случайной, стратифицированной, кластерной и квотной);
корреляционного и регрессионного анализа — выявляет взаимосвязи данных и причины, по которым данные зависят друг от друга, определяет силу этой зависимости;
метода динамических рядов — отслеживает силу, интенсивность и частоту изменений объектов и явлений; позволяет оценить данные во времени и дает возможность прогнозирования явлений.

Статистические исследования могут проводить маркетологи-аналитики:

Для качественного анализа статистических данных необходимо либо обладать знаниями математической статистики, либо использовать отчетно-аналитическую программу, либо не заниматься этим. Европейские компании давно осознали пользу такого анализа, поэтому либо нанимают хороших аналитиков с математическим образованием, либо устанавливают профессиональное программное обеспечение для аналитиков-маркетологов. Ежедневный анализ в этих компаниях помогает им правильно организовывать закупку товаров, их хранение и логистику, корректировать количество персонала и их рабочие графики.

Решения для автоматизации анализа данных позволяют работать с ними аналитикам-маркетологам. Сегодня есть решения, доступные даже небольшим компаниям, такие как Tableau. Их преимущества по сравнению с анализом, проведенным исключительно человеком:

невысокая стоимость внедрения (от 2000 рублей в месяц – на февраль 2018 года),
современное графическое представление анализа,
возможность мгновенно переходить от одного, более полного отчета, к другому, более детальному.

Хотите узнать, как провести анализ и сделать отчеты быстро?

источник

«Человек, который напрямую влияет на решения бизнеса»

Данные собирают все — от магазинов и ресторанов до компаний-монополистов и приложений с миллионной аудиторией. Аналитик данных помогает сделать так, чтобы собранная информация приносила пользу бизнесу. Мы выяснили, какие задачи вместе с экспертами решает такой специалист и почему ему нужно разбираться в бизнес-процессах не хуже владельца компании.

Аналитик данных (или дата-аналитик) — это специалист, который собирает, обрабатывает, изучает и интерпретирует данные. Его работа помогает принимать решения в бизнесе, управлении и науке. Обычно такие специалисты работают в компаниях, которые практикуют data-driven подход — ориентируются на данные и их анализ при принятии решений. Курс «Аналитик данных» Яндекс.Практикума рассчитан именно на это направление.

«Любой продукт, у которого есть аудитория, собирает данные. Аналитика есть в телекоме, банках, играх, консалтинге. Если сильно обобщить, то можно сказать так: там, где есть возможность сохранять данные о продукте и поведении пользователя, рано или поздно должен появиться аналитик», — говорит Анна Чувилина, автор и менеджер программы «Аналитик данных».

Аналитик данных — важный участник бизнеса, потому что обеспечивает уверенность в принятии решений. Создавать новый продукт очень дорого, а ошибка при внедрении новой функции может стоить компании репутации и прибыли. Дата-аналитики проводят А/B-тесты и строят модели, чтобы проверить, как пользователи или клиенты реагируют на нововведения, и оценить перспективы того или иного проекта. Это дешевле и снижает риски бизнеса. Чтобы делать свою работу хорошо, аналитик должен видеть бизнес-процессы. Поэтому важно, чтобы он мог влиять на процесс принятия решения, основываясь на результатах своих исследований. Иначе работа такого специалиста теряет ценность.

Хороший аналитик данных — не просто математик с навыками программиста. Он понимает бизнес-процессы и хорошо знает продукт. Такой специалист разбирается, на чем зарабатывает конкретный бизнес. В результате его работы компания может получать больше прибыли и делать своих пользователей счастливее. Сильный аналитик данных прежде чем взяться за работу всегда спрашивает руководителя о том, какую задачу хочет решить бизнес.

Кроме программных инструментов аналитику данных важно развивать — метапрофессиональные умения, которые помогают делать работу лучше. Это способность налаживать общение с коллегами и партнерами, умение решать проблемы и выходить из конфликтных ситуаций с наименьшими потерями, сильный эмоциональный интеллект. Такие навыки больше связаны с личностью человека, чем с его профессиональным уровнем. Но их тоже можно формировать и развивать.

«Важно не путать дата-саентиста и дата-аналитика. Первый — это программист, знающий определенный набор языков и алгоритмов. Он решает поставленную техническую задачу. А дата-аналитик ставит эту задачу и переводит результат на язык бизнеса. Для этого нужно развивать гибкие навыки: работа с требованиями, визуализация данных, переговоры. То есть понимать самому и уметь объяснить, что дает бизнесу ваша аналитика. Изучить программы недостаточно — нужно критически подходить к задаче», — говорит Алексей Колоколов, эксперт по BI и визуализации данных.

Для каждого бизнеса задачи будут свои, а порядок действий общий. Аналитик данных работает так:

собирает данные (формирует запрос сам или получает задачу от менеджеров);
знакомится с параметрами набора (какие типы данных собраны, как их можно отсортировать);
проводит предварительную обработку (очищает от ошибок и повторов, упорядочивает);
интерпретирует (анализирует, собственно решает задачу);
делает вывод;
визуализирует (так, чтобы на основе вывода можно было принять решение, подтвердить или опровергнуть гипотезу).

Типичные задачи, с которыми приходят к дата-аналитику:

Получить выгрузку данных для определенных целей
Бухгалтерии нужен список сотрудников, у которых в семье пятеро детей, — специалист делает выгрузку из базы данных.
Ответить на вопрос бизнеса
Сделать расчет определенной метрики: сколько сотрудников уволилось до конца испытательного срока в этом году и сколько в предыдущем. Если компания вводит новую систему адаптации, то изменения такой метрики покажут результат.
Провести А/B-тестирование
Нужно выяснить, как пользователи реагируют на то, какого цвета кнопка, зеленого или красного. Аналитик тестирует два прототипа. Часть пользователей видят прототип с зеленой кнопкой, другие — с красной. Он смотрит, как реагировали пользователи, проверяет, было ли различие статистически значимо. В итоге — рекомендует решение, которое проверил в ходе теста: внедрить зеленую или красную кнопку.
Провести исследования
Конкретного вопроса от бизнеса нет, но нужен ресерч: взять внешние или внутренние данные, исследовать, найти аномалии или инсайты, провести пиар-исследование.
Просчитать, какой вариант выгоднее
Юнит-экономика: расчет РОИ, инвестиционного потенциала. Оценить окупаемость рекламной кампании или скорректировать бизнес-модель.
Выяснить, какой товар и в какое время больше покупают
Взять группу товаров и посмотреть, есть ли сезонные всплески интереса, сравнить с другими группами.

Статистика позволяет сделать общие выводы по конкретному вопросу. А аналитика данных — исследовать тему со всех сторон, сравнить решения, найти аномалии или инсайты, сопоставить события по множеству параметров. Это открывает новые возможности для бизнеса.

Дата-аналитик может исследовать внутренние данные компании или обратиться к внешним источникам. Анализ открытых данных позволяет отслеживать важные социальные и культурные тренды.

«Дата-аналитик может глубже исследовать проблему. Например, в наших данных по ДТП в России есть доля водителей, которые нарушили правила ОСАГО. Зная эту долю и то, как она менялась в разные годы, мы можем делать выводы о социально-экономической ситуации в регионе — видим тенденцию, когда водители перестают покупать полисы, потому что у них нет денег.

Из того же датасета мы вытаскивали информацию про скрывшихся водителей. Оказалось, что в Омской области 20% водителей покидают место ДТП. Получив эту информацию, мы можем задавать дополнительные вопросы: почему так происходит, что это за социальные и культурные процессы», — рассказывает Сергей Устинов, аналитик данных и проджект-менеджер.

Стереотипы в сфере аналитики данных не работают — неважно, гуманитарное или техническое образование получил дата-аналитик.

«У меня нет технического образования, я учился на факультете госуправления. А Python изучал на курсе биоинформатики для биологов. На мой взгляд, этот язык больше всего подходит для старта, база навыков работы с ним приобретается за два-три месяца. Затем стоит изучать профильные библиотеки для сбора и анализа данных. Чем больше ты знаешь библиотек, тем более качественная аналитика тебе доступна», — говорит Сергей Устинов.

Компании не рассчитывают, что начинающий аналитик данных будет уметь сразу всё. Они готовы обучать и направлять молодого специалиста. Главное — интерес к решению бизнес-задач. Правильно сформулированный перед исследованием вопрос важнее, чем большой опыт работы с программными инструментами.

«Программирование и математику можно выучить. А софтскиллы — нарабатываются опытом и практикой. Поэтому дата-аналитику полезны хакатоны и чемпионаты с решением практических задач. Он увереннее чувствует себя, прокачивая стиль мышления, ориентированный на решение конкретных бизнес-задач», — говорит Анна Чувилина.

Начинающих специалистов в сфере ИТ охотнее всего берут на позиции, связанные с анализом данных: доля вакансий для кандидатов с опытом работы меньше года здесь на четверть выше, чем в целом по рынку.

Работодатели ждут, что начинающий специалист:

знает хотя бы один язык программирования: Python или R;
умеет писать запросы к базам данных SQL;
может показать выводы и метрики в виде понятного дашборда (Tableau, Power BI, Amplitude);
хочет разбираться в бизнес-процессах, мыслит в терминах бизнес-задач.

Аналитику данных нужно понимать, что такое статистика и гипотеза. Серьезная математика не пригодится, главное ориентироваться в понятиях. В зависимости от запроса компании могут понадобиться навыки работы с Яндекс.Метрикой или Google Analytics. Опытные программисты с сильной математикой, которые не готовы думать в терминах задач бизнеса, закрывают себе путь в профессию аналитика данных.

«Джуниор вырастает в крутого специалиста, решая реальные кейсы. Потому что насмотренность определяет твой уровень: важно, сколько раз жизнь ставила тебя в ситуацию, когда нужно принимать решение. Развиваться в том, как владеешь инструментами, тоже важно. Но и решение реальных задач помогает аналитику данных расти», — говорит Анна Чувилина.

источник

Деятельность людей во множестве случаев предполагает работу с данными, а она в свою очередь может подразумевать не только оперирование ими, но и их изучение, обработку и анализ. Например, когда нужно уплотнить информацию, найти какие-то взаимосвязи или определить структуры. И как раз для аналитики в этом случае очень удобно пользоваться не только разными техниками мышления, но и применять статистические методы.

Особенностью методов статистического анализа является их комплексность, обусловленная многообразием форм статистических закономерностей, а также сложностью процесса статистических исследований. Однако мы хотим поговорить именно о таких методах, которые может применять каждый, причем делать это эффективно и с удовольствием.

Статистическое исследование может проводиться посредством следующих методик:

Статистическое наблюдение;
Сводка и группировка материалов статистического наблюдения;
Абсолютные и относительные статистические величины;
Вариационные ряды;
Выборка;
Корреляционный и регрессионный анализ;
Ряды динамики.

Далее мы рассмотрим каждый из них более подробно. Но отметим, что представим лишь основные характеристики без подробного описания алгоритмов действий. Впрочем, понять их не составит никакого труда.

Статистическое наблюдение является планомерным, организованным и в большинстве случаев систематическим сбором информации, направленным, главным образом, на явления социальной жизни. Реализуется данный метод через регистрацию предварительно определенных наиболее ярких признаков, цель которой состоит в последующем получении характеристик изучаемых явлений.

Статистическое наблюдение должно выполняться с учетом некоторых важных требований:

Оно должно полностью охватывать изучаемые явления;
Получаемые данные должны быть точными и достоверными;
Получаемые данные должны быть однообразными и легкосопоставимыми.

Также статистическое наблюдение может иметь две формы:

Отчетность – это такая форма статистического наблюдения, где информация поступает в конкретные статистические подразделения организаций, учреждений или предприятий. В этом случае данные вносятся в специальные отчеты.
Специально организованное наблюдение – наблюдение, которое организуется с определенной целью, чтобы получить сведения, которых не имеется в отчетах, или же для уточнения и установления достоверности информации отчетов. К этой форме относятся опросы (например, опросы мнений людей), перепись населения и т.п.

Кроме того, статистическое наблюдение может быть категоризировано на основе двух признаков: либо на основе характера регистрации данных, либо на основе охвата единиц наблюдения. К первой категории относятся опросы, документирование и прямое наблюдение, а ко второй – наблюдение сплошное и несплошное, т.е. выборочное.

Для получения данных при помощи статистического наблюдения можно применять такие способы как анкетирование, корреспондентская деятельность, самоисчисление (когда наблюдаемые, например, сами заполняют соответствующие документы), экспедиции и составление отчетов.

Говоря о втором методе, в первую очередь следует сказать о сводке. Сводка представляет собой процесс обработки определенных единичных фактов, которые образуют общую совокупность данных, собранных при наблюдении. Если сводка проводится грамотно, огромное количество единичных данных об отдельных объектах наблюдения может превратиться в целый комплекс статистических таблиц и результатов. Также такое исследование способствует определению общих черт и закономерностей исследуемых явлений.

С учетом показателей точности и глубины изучения можно выделить простую и сложную сводку, но любая из них должна основываться на конкретных этапах:

Выбирается группировочный признак;
Определяется порядок формирования групп;
Разрабатывается система показателей, позволяющих охарактеризовать группу и объект или явление в целом;
Разрабатываются макеты таблиц, где будут представлены результаты сводки.

Важно заметить, что есть и разные формы сводки:

Централизованная сводка, требующая передачи полученного первичного материала в вышестоящий центр для последующей обработки;
Децентрализованная сводка, где изучение данных происходит на нескольких ступенях по восходящей.

Выполняться же сводка может при помощи специализированного оборудования, например, с использованием компьютерного ПО или вручную.

Что же касается группировки, то этот процесс отличается разделением исследуемых данных на группы по признакам. Особенности поставленных статистическим анализом задач влияют на то, какой именно будет группировка: типологической, структурной или аналитической. Именно поэтому для сводки и группировки либо прибегают к услугам узкопрофильных специалистов, либо применяют конкретные техники мышления.

Абсолютные величина считаются самой первой формой представления статистических данных. С ее помощью удается придать явлениям размерные характеристики, например, по времени, по протяженности, по объему, по площади, по массе и т.д.

Если требуется узнать об индивидуальных абсолютных статистических величинах, можно прибегнуть к замерам, оценке, подсчету или взвешиванию. А если нужно получить итоговые объемные показатели, следует использовать сводку и группировку. Нужно иметь в виду, что абсолютные статистические величины отличаются наличием единиц измерения. К таким единицам относят стоимостные, трудовые и натуральные.

А относительные величины выражают количественные соотношения, касающиеся явлений социальной жизни. Чтобы их получить, одни величины всегда делятся на другие. Показатель, с которым сравнивают (это знаменатель), называют основанием сравнения, а показатель, которой сравнивают (это числитель), называют отчетной величиной.

Относительные величины могут быть разными, что зависит от их содержательной части. Например, существуют величины сравнения, величины уровня развития, величины интенсивности конкретного процесса, величины координации, структуры, динамики и т.д. и т.п.

Чтобы изучить какую-то совокупность по дифференцирующимся признакам, в статистическом анализе применяются средние величины – обобщающие качественные характеристики совокупности однородных явлений по какому-либо дифференцирующемуся признаку.

Крайне важным свойством средних величин является то, что они говорят о значениях конкретных признаков во всем их комплексе единым числом. Невзирая на то, что у отдельных единиц может наблюдаться количественная разница, средние величины выражают общие значения, свойственные всем единицам исследуемого комплекса. Получается, что при помощи характеристики чего-то одного можно получить характеристику целого.

Следует иметь в виду, что одним из самых важных условий применения средних величин, если проводится статистический анализ социальных явлений, считается однородность их комплекса, для которого и нужно узнать среднюю величину. А от такого, как именно будут представлены начальные данные для исчисления средней величины, будет зависеть и формула ее определения.

В некоторых случаях данных о средних показателях тех или иных изучаемых величин может быть недостаточно, чтобы провести обработку, оценку и глубокий анализ какого-то явления или процесса. Тогда во внимание следует брать вариацию или разброс показателей отдельных единиц, который тоже представляет собой важную характеристику исследуемой совокупности.

На индивидуальные значения величин могут воздействовать многие факторы, а сами изучаемые явления или процессы могут быть очень многообразны, т.е. обладать вариацией (это многообразие и есть вариационные ряды), причины которой следует искать в сущности того, что изучается.

Вышеназванные абсолютные величины находятся в непосредственной зависимости от единиц измерения признаков, а значит, делают процесс изучения, оценки и сравнения двух и более вариационных рядов более сложным. А относительные показатели нужно вычислять в качестве соотношения абсолютных и средних показателей.

Смысл выборочного метода (или проще – выборки) состоит в том, что по свойствам одной части определяются численные характеристики целого (это называется генеральной совокупностью). Основной выборочного метода является внутренняя связь, объединяющая части и целое, единичное и общее.

Метод выборки отличается рядом существенных преимуществ перед остальными, т.к. благодаря уменьшению количества наблюдений позволяет сократить объемы работы, затрачиваемые средства и усилия, а также успешно получать данные о таких процессах и явлениях, где либо нецелесообразно, либо просто невозможно исследовать их полностью.

Соответствие характеристик выборки характеристикам изучаемого явления или процесса будет зависеть от комплекса условий, и в первую очередь от того, как вообще будет реализовываться выборочный метод на практике. Это может быть как планомерный отбор, идущий по подготовленной схеме, так и непланомерный, когда выборка производится из генеральной совокупности.

Но во всех случаях выборочный метод должен быть типичным и соответствовать критериям объективности. Данные требования нужно выполнять всегда, т.к. именно от них будет зависеть соответствие характеристик метода и характеристик того, что подвергается статистическому анализу.

Таким образом, перед обработкой выборочного материала необходимо провести его тщательную проверку, избавившись тем самым от всего ненужного и второстепенного. Одновременно с этим, составляя выборку, в обязательном порядке нужно обходить стороной любую самодеятельность. Это означает, что ни в коем случае не следует делать выборку только из вариантов, кажущихся типичными, а все другие – отбрасывать.

Эффективная и качественная выборка должна составляться объективно, т.е. производить ее нужно так, чтобы были исключены любые субъективные влияния и предвзятые побуждения. И чтобы это условие было соблюдено должным образом, требуется прибегнуть к принципу рандомизации или, проще говоря, к принципу случайного отбора вариантов из всей их генеральной совокупности.

Представленный принцип служит основой теории выборочного метода, и следовать ему нужно всегда, когда требуется создать эффективную выборочную совокупность, причем случаи планомерного отбора исключением здесь не являются.

Корреляционный анализ и регрессионный анализ – это два высокоэффективных метода, позволяющие проводить анализ больших объемов данных для изучения возможной взаимосвязи двух или большего количества показателей.

В случае с корреляционным анализом задачами являются:

Измерить тесноту имеющейся связи дифференцирующихся признаков;
Определить неизвестные причинные связи;
Оценить факторы, в наибольшей степени воздействующие на окончательный признак.

А в случае с регрессионным анализом задачи следующие:

Определить форму связи;
Установить степень воздействия независимых показателей на зависимый;
Определить расчетные значения зависимого показателя.

Чтобы решить все вышеназванные задачи, практически всегда нужно применять и корреляционный и регрессионный анализ в комплексе.

Посредством этого метода статистического анализа очень удобно определять интенсивность или скорость, с которой развиваются явления, находить тенденцию их развития, выделять колебания, сравнивать динамику развития, находить взаимосвязь развивающихся во времени явлений.

Ряд динамики – это такой ряд, в котором во времени последовательно расположены статистические показатели, изменения которых характеризуют процесс развития исследуемого объекта или явления.

Ряд динамики включает в себя два компонента:

Период или момент времени, связанный с имеющимися данными;
Уровень или статистический показатель.

В совокупности эти компоненты представляют собой два члена ряда динамики, где первый член (временной период) обозначается буквой «t», а второй (уровень) – буквой «y».

Исходя из длительности временных промежутков, с которыми взаимосвязаны уровни, ряды динамики могут быть моментными и интервальными. Интервальные ряды позволяют складывать уровни для получения общей величины периодов, следующих один за другим, а в моментных такой возможности нет, но этого там и не требуется.

Ряды динамики также существуют с равными и разными интервалами. Суть же интервалов в моментных и интервальных рядах всегда разная. В первом случае интервалом является временной промежуток между датами, к которым привязаны данные для анализа (удобно использовать такой ряд, например, для определения количества действий за месяц, год и т.д.). А во втором случае – временной промежуток, к которому привязана совокупность обобщенных данных (такой ряд можно использовать для определения качества тех же самых действий за месяц, год и т.п.). Интервалы могут быть равными и разными, независимо от типа ряда.

Естественно, чтобы научиться грамотно применять каждый из методов статистического анализа, недостаточно просто знать о них, ведь, по сути, статистика – это целая наука, требующая еще и определенных навыков и умений. Но чтобы она давалась проще, можно и нужно тренировать свое мышление и улучшать когнитивные способности.

В остальном же исследование, оценка, обработка и анализ информации – очень интересные процессы. И даже в тех случаях, когда это не приводит к какому-то конкретному результату, за время исследования можно узнать множество интересных вещей. Статистический анализ нашел свое применение в огромном количестве сфер деятельности человека, а вы можете использовать его в учебе, работе, бизнесе и других областях, включая развитие детей и самообразование.

источник

Статистика и анализ данных пронизывают практически любую современную область знаний. Все сложнее становится провести границу между современной биологией, математикой и информатикой. Экономические исследования и регрессионный анализ уже практически неотделимы друг от друга. Один из известных методов проверки распределения на нормальность — критерий Колмогорова-Смирнова. А вы знали, что именно Колмогоров внес огромный вклад в развитие математической лингвистики?

Еще будучи студентом психологического факультета СПбГУ, я заинтересовался когнитивной психологией. Кстати, Иммануил Кант не считал психологию наукой, так как не видел возможности применять в ней математические методы. Мои текущие исследования посвящены моделированию психических процессов, и я надеюсь, что такие направления в современной когнитивной психологии, как вычислительные и коннективисткие модели, смягчили бы его отношение!

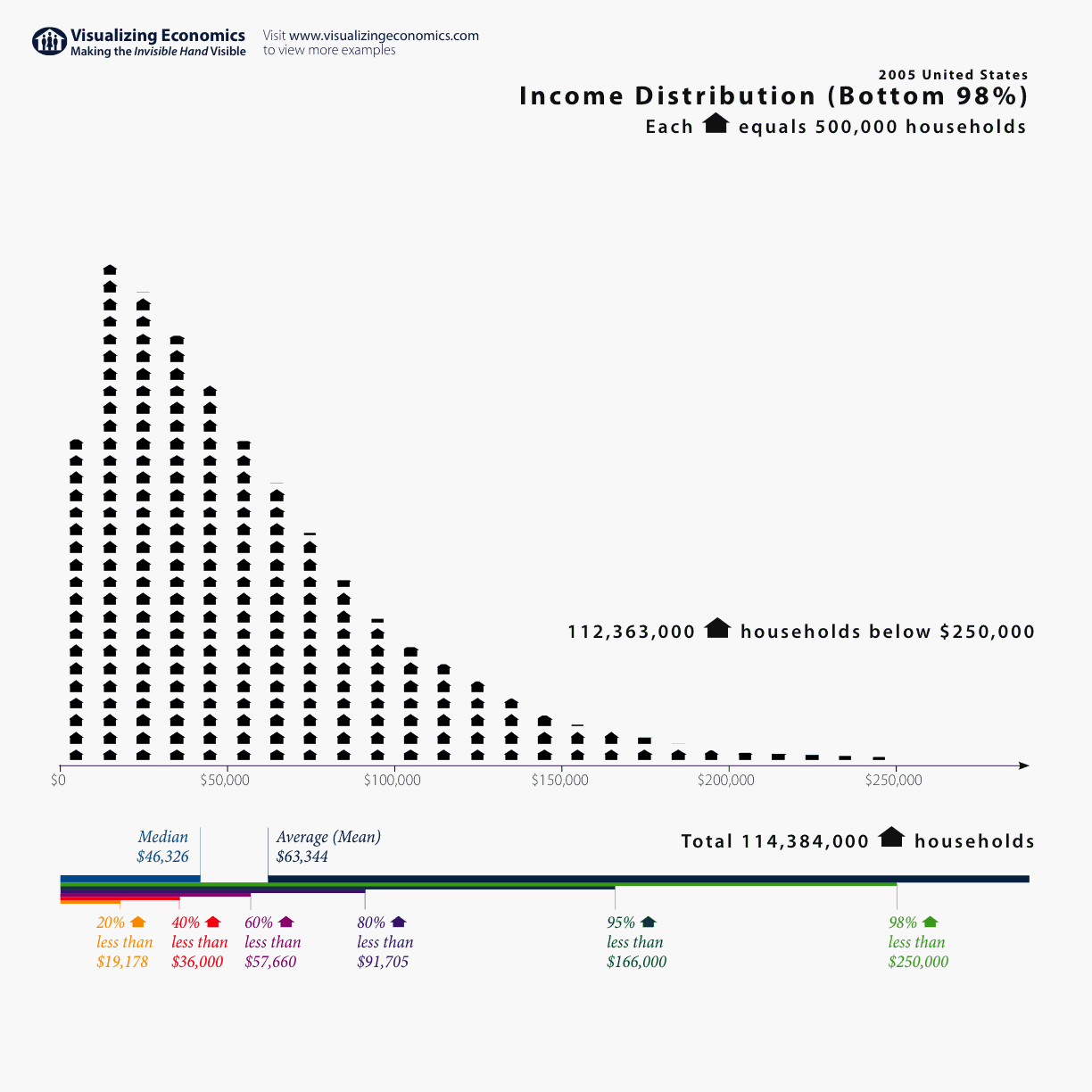
Конечно, статистика применяется далеко за пределами научных лабораторий: в рекламе, маркетинге, бизнесе, медицине, образовании и т.д. Но, что самое интересное, базовые знания анализа данных крайне полезны и в повседневной жизни. Например, думаю, все вы знакомы с понятием среднего арифметического. Среднее значение очень часто используется в СМИ при обсуждении различных социально-экономических показателей — доходов, уровня безработицы и т.д. В 2005 году британские СМИ писали о том, что средний уровень дохода населения не только не возрос, но снизился на 0,2 % по сравнению с предыдущим годом. Мелькали заголовки «Доходы населения снизились впервые с 1990 года». Некоторые политики даже использовали этот факт, критикуя действующее правительство. Однако, важно понимать, что среднее арифметическое — хороший показатель, когда наш признак имеет симметричное распределение (богатых столько же, сколько бедных). Реальное же распределение доходов имеет скорее следующий вид:

Распределение имеет явно выраженную асимметрию: очень состоятельных людей заметно меньше, чем представителей среднего класса. Это приводит к тому, что в данном случае банкротство одного из миллионеров может значительно повлиять на этот показатель. Гораздо информативнее использовать значение медианы для описания таких данных. Медиана — это значение зарплаты, которое находится в самой середине распределения доходов (50% всех наблюдений меньше медианы, 50% — больше). И, как ни удивительно, медиана дохода в 2005 году в Великобритании, в отличие от среднего значения, продолжила свой рост. Таким образом, если вы знаете о различных типах распределения и различных мерах центральной тенденции (среднее и медиана), то вас не так просто ввести в заблуждение в таких случаях, как описаны в примере.

Как мы уже выяснили, чем бы вы ни планировали заниматься, вероятность столкнуться с курсом «математическая статистика в вашей области» постепенно приближается к единице. Однако, часто занятия по введению в статистику не вызывают восторга у студентов нетехнических факультетов. Через несколько занятий выясняется, что такие базовые понятия, как, например, корреляция представляют собой нечто следующее:

И, отчаявшись досконально разобраться с происхождением этих сумм и квадратных корней, студент может начать воспринимать статистику следующим образом: «если r > 0, то положительная связь, а если меньше 0, то отрицательная»; «если p уровень значимости меньше 0.05 — то хорошо, если от 0.05 до 0.1 — то не очень хорошо, а если больше 0.1 — то плохо». Помогая студентам готовиться к экзамену, не раз сталкивался с такими заклинаниями! Также, разумеется, никто не рассчитывает все эти показатели вручную, и используя, например, SPSS, можно за секунду загуглить пошаговую инструкцию «как сравнить два средних».

Жмем сюда
Снимаем/ставим галочки тут
p profit

Статистический анализ начинает напоминать черный ящик: на вход подаются данные, на выход — таблица основных результатов и значение p-уровня значимости (p-value), который и расставит все точки над i.

Предположим, мы решили выяснить, существует ли взаимосвязь между пристрастием к кровавым компьютерным играм и агрессивностью в реальной жизни. Для этого были случайным образом сформированы две группы школьников по 100 человек в каждой (1 группа — фанаты стрелялок, вторая группа — не играющие в компьютерные игры). В качестве показателя агрессивности выступает, например, число драк со сверстниками. В нашем воображаемом исследовании оказалось, что группа школьников-игроманов действительно заметно чаще конфликтует с товарищами. Но как нам выяснить, насколько статистически достоверны полученные различия? Может быть, мы получили наблюдаемую разницу совершенно случайно? Для ответа на эти вопросы и используется значение p-уровня значимости (p-value) — это вероятность получить такие или более выраженные различия при условии, что в генеральной совокупности никаких различий на самом деле нет. Иными словами, это вероятность получить такие или еще более сильные различия между нашими группами, при условии, что, на самом деле, компьютерные игры никак не влияют на агрессивность. Звучит не так уж и сложно. Однако, именно этот статистический показатель очень часто интерпретируется неправильно.

Итак, мы сравнили две группы школьников между собой по уровню агрессивности при помощи стандартного t-теста (или непараметрического критерия Хи — квадрат более уместного в данной ситуации) и получили, что заветный p-уровень значимости меньше 0.05 (например 0.04). Но о чем в действительности говорит нам полученное значение p-уровня значимости? Итак, если p-value — это вероятность получить такие или более выраженные различия при условии, что в генеральной совокупности никаких различий на самом деле нет, то какое, на ваш взгляд, верноеутверждение:

Компьютерные игры — причина агрессивного поведения с вероятностью 96%.
Вероятность того, что агрессивность и компьютерные игры не связаны, равна 0.04.
Если бы мы получили p-уровень значимости больше, чем 0.05, это означало бы, что агрессивность и компьютерные игры никак не связаны между собой.
Вероятность случайно получить такие различия равняется 0.04.
Все утверждения неверны.

Если вы выбрали пятый вариант, то абсолютно правы! Но, как показывают многочисленные исследования, даже люди со значительным опытом в анализе данных часто некорректно интерпретируют значение p-value (например, можно посмотреть эту интересную статью).

Первое утверждение — пример ошибки корреляции: факт значимой взаимосвязи двух переменных ничего не говорит нам о причинах и следствиях. Может быть, это более агрессивные люди предпочитают проводить время за компьютерными играми, а вовсе не компьютерные игры делают людей агрессивнее.
Это уже более интересное утверждение. Все дело в том, что мы изначально принимаем за данное, что никаких различий на самом деле нет. И, держа это в уме как факт, рассчитываем значение p-value. Поэтому правильная интерпретация: «Если предположить, что агрессивность и компьютерные игры никак не связаны, то вероятность получить такие или еще более выраженные различия составила 0.04».
А что делать, если мы получили незначимые различия? Значит ли это, что никакой связи между исследуемыми переменными нет? Нет, это означает лишь то, что различия, может быть, и есть, но наши результаты не позволили их обнаружить.
Это напрямую связано с самим определением p-value. 0.04 — это вероятность получить такие или еще более экстремальные различия. Оценить вероятность получить именно такие различия, как в нашем эксперименте, в принципе невозможно!

Вот такие подводные камни могут скрываться в интерпретации такого показателя, как p-value. Поэтому очень важно понимать механизмы, заложенные в основании методов анализа и расчета основных статистических показателей.

Сейчас я пишу диссертацию на факультете психологии СПбГУ и преподаю статистику биологам в Институте биоинформатики. Основываясь на курсе читаемых лекций и собственного исследовательского опыта, возникла идея создать онлайн-курс по введению в статистику на русском языке для всех желающих, необязательно биоинформатиков или биологов.

Существует много хороших онлайн-курсов по анализу данных и статистике (например, такой, такой, или такой), но практически все они на английском языке. Надеюсь, что курс будет полезен для тех, кто только знакомится с основами статистики. В нем я стараюсь в максимально доступной форме разобрать основные идеи и методы анализа данных, уделяя особое внимание самой идее статистической проверки гипотез и интерпретации получаемых результатов. В качестве примеров будут задачи из различных областей: от биоинформатики до социологии. Курс бесплатный и все его материалы останутся открытыми после окончания, начинается 15 февраля.

источник

После завершения любого научного исследования, фундаментального или экспериментального, производится статистический анализ полученных данных. Чтобы статистический анализ был успешно проведен и позволил решить поставленные задачи, исследование должно быть грамотно спланировано. Следовательно, без понимания основ статистики невозможно планирование и обработка результатов научного эксперимента. Тем не менее, медицинское образование не дает не только знания статистики, но даже основ высшей математики. Поэтому очень часто можно столкнуться с мнением, что вопросами статобработки в биомедицинских исследованиях должен заниматься только специалист по статистике, а врачу-исследователю следует сосредоточиться на медицинских вопросах своей научной работы. Подобное разделение труда, подразумевающее помощь в анализе данных, вполне оправдано. Однако понимание принципов статистики необходимо хотя бы для того, чтобы избежать некорректной постановки задачи перед специалистом, общение с которым до начала исследования является в такой же степени важным, как и на этапе обработки данных.

Прежде чем говорить об основах статистического анализа, следует прояснить смысл термина «статистика». Существует множество определений, но наиболее полным и лаконичным является, на наш взгляд, определение статистики как «науки о сборе, представлении и анализе данных». В свою очередь, использование статистики в приложении к живому миру называют «биометрией» или «биостатистикой».

Следует заметить, что очень часто статистику сводят только к обработке экспериментальных данных, не обращая внимания на этап их получения. Однако статистические знания необходимы уже во время планирования эксперимента, чтобы полученные в ходе него показатели могли дать исследователю достоверную информацию. Поэтому, можно сказать, что статистический анализ результатов эксперимента начинается еще до начала исследования.

Уже на этапе разработки плана исследователь должен четко представлять себе, какого типа переменные будут в его работе. Все переменные можно разделить на два класса: качественные и количественные. То, какой диапазон может принимать переменная, зависит от шкалы измерений. Можно выделить четыре основных шкалы:

1. номинальную;
2. ординальную;
3. интервальную;
4. рациональную (шкалу отношений).

В номинальной шкале (шкале «названий») присутствуют лишь условные обозначения для описания некоторых классов объектов, например, «пол» или «профессия пациента». Номинальная шкала подразумевает, что переменная будет принимать значения, количественные взаимоотношения между которыми определить невозможно. Так, невозможно установить математические отношения между мужским и женским полом. Условные числовые обозначения (женщины — 0, мужчины — 1, либо наоборот) даются абсолютно произвольно и предназначены только для компьютерной обработки. Номинальная шкала является качественной в чистом виде, отдельные категории в этой шкале выражают частотами (количество или доля наблюдений, проценты).

Ординальная (порядковая) шкала предусматривает, что отдельные категории в ней могут выстраиваться по возрастанию или убыванию. В медицинской статистике классическим примером порядковой шкалы является градация степеней тяжести заболевания. В данном случае мы можем выстроить тяжесть по возрастанию, но все еще не имеем возможности задать количественные взаимоотношения, т. е. дистанция между значениями, измеренными в ординальной шкале, неизвестна или не имеет значения. Установить порядок следования значений переменной «степень тяжести» легко, но при этом невозможно определить, во сколько раз тяжелое состояние отличается от состояния средней тяжести.

Ординальная шкала относится к полуколичественным типам данных, и ее градации можно описывать как частотами (как в качественной шкале), так и мерами центральных значений, на чем мы остановимся ниже.

Интервальная и рациональная шкалы относятся к чисто количественным типам данных. В интервальной шкале мы уже можем определить, насколько одно значение переменной отличается от другого. Так, повышение температуры тела на 1 градус Цельсия всегда означает увеличение выделяемой теплоты на фиксированное количество единиц. Однако в интервальной шкале есть и положительные и отрицательные величины (нет абсолютного нуля). В связи с этим невозможно сказать, что 20 градусов Цельсия — это в два раза теплее, чем 10. Мы можем лишь констатировать, что 20 градусов настолько же теплее 10, как 30 — теплее 20.

Рациональная шкала (шкала отношений) имеет одну точку отсчета и только положительные значения. В медицине большинство рациональных шкал — это концентрации. Например, уровень глюкозы 10 ммоль/л — это в два раза большая концентрация по сравнению с 5 ммоль/л. Для температуры рациональной шкалой является шкала Кельвина, где есть абсолютный ноль (отсутствие тепла).

Следует добавить, что любая количественная переменная может быть непрерывной, как в случае измерения температуры тела (это непрерывная интервальная шкала), или же дискретной, если мы считаем количество клеток крови или потомство лабораторных животных (это дискретная рациональная шкала).

Указанные различия имеют решающее значение для выбора методов статистического анализа результатов эксперимента. Так, для номинальных данных применим критерий «хи-квадрат», а известный тест Стьюдента требует, чтобы переменная (интервальная либо рациональная) была непрерывной.

После того как будет решен вопрос о типе переменной, следует заняться формированием выборки. Выборка — это небольшая группа объектов определенного класса (в медицине — популяция). Для получения абсолютно точных данных нужно исследовать все объекты данного класса, однако, из практических (зачастую — финансовых) соображений изучают только часть популяции, которая и называется выборкой. В дальнейшем, статистический анализ позволяет исследователю распространить полученные закономерности на всю популяцию с определенной степенью точности. Фактически, вся биомедицинская статистика направлена на получение наиболее точных результатов из наименее возможного количества наблюдений, ведь при исследованиях на людях важен и этический момент. Мы не можем позволить себе подвергать риску большее количество пациентов, чем это необходимо.

Создание выборки регламентируется рядом обязательных требований, нарушение которых может привести к ошибочным выводам из результатов исследования. Во-первых, важен объем выборки. От объема выборки зависит точность оценки исследуемых параметров. Здесь следует обратить внимание на слово «точность». Чем больше размеры исследуемых групп, тем более точные (но не обязательно правильные) результаты получает ученый. Для того же, чтобы результаты выборочных исследований можно было переносить на всю популяцию в целом, выборка должна быть репрезентативной. Репрезентативность выборки предполагает, что в ней отражены все существенные свойства популяции. Другими словами, в исследуемых группах лица разного пола, возраста, профессий, социального статуса и пр. встречаются с той же частотой, что и во всей популяции.

Однако перед тем как начать выбор исследуемой группы, следует определиться с необходимостью изучения конкретной популяции. Примером популяции могут быть все пациенты с определенной нозологией или люди трудоспособного возраста и т. д. Так, результаты, полученные для популяции молодых людей призывного возраста, вряд ли удастся экстраполировать на женщин в постменопаузе. Набор характеристик, которые будет иметь изучаемая группа, определяет «обобщаемость» данных исследования.

Формировать выборки можно различными путями. Самый простой из них — выбор с помощью генератора случайных чисел необходимого количества объектов из популяции или выборочной рамки (sampling frame). Такой способ называется «простой случайной выборкой». Если случайным образом выбрать начальную точку в выборочной рамке, а затем взять каждый второй, пятый или десятый объекты (в зависимости от того каких размеров группы требуются в исследовании), то получится интервальная выборка. Интервальная выборка не является случайной, так как никогда не исключается вероятность периодических повторений данных в рамках выборочной рамки.

Возможен вариант создания так называемой «стратифицированной выборки», которая предполагает, что популяция состоит из нескольких различных групп и эту структуру следует воспроизвести в экспериментальной группе. Например, если в популяции соотношение мужчин и женщин 30:70, тогда в стратифицированной выборке их соотношение должно быть таким же. При данном подходе критически важно не балансировать выборку избыточно, то есть избежать однородности ее характеристик, в противном случае исследователь может упустить шанс найти различия или связи в данных.

Кроме описанных способов формирования групп есть еще кластерная и квотная выборки. Первая используется в случае, когда получение полной информации о выборочной рамке затруднено из-за ее размеров. Тогда выборка формируется из нескольких групп, входящих в популяцию. Вторая — квотная — аналогична стратифицированной выборке, но здесь распределение объектов не соответствует таковому в популяции.

Возвращаясь к объему выборки, следует сказать, что он тесно связан с вероятностью статистических ошибок первого и второго рода. Статистические ошибки могут быть обусловлены тем, что в исследовании изучается не вся популяция, а ее часть. Ошибка первого рода — это ошибочное отклонение нулевой гипотезы. В свою очередь, нулевая гипотеза — это предположение о том, что все изучаемые группы взяты из одной генеральной совокупности, а значит, различия либо связи между ними случайны. Если провести аналогию с диагностическими тестами, то ошибка первого рода представляет собой ложноположительный результат.

Ошибка второго рода — это неверное отклонение альтернативной гипотезы, смысл которой заключается в том, что различия либо связи между группами обусловлены не случайным совпадением, а влиянием изучаемых факторов. И снова аналогия с диагностикой: ошибка второго рода — это ложноотрицательный результат. С этой ошибкой связано понятие мощности, которое говорит о том, насколько определенный статистический метод эффективен в данных условиях, о его чувствительности. Мощность вычисляется по формуле: 1-β, где β — это вероятность ошибки второго рода. Данный показатель зависит преимущественно от объема выборки. Чем больше размеры групп, тем меньше вероятность ошибки второго рода и выше мощность статистических критериев. Зависимость эта как минимум квадратичная, то есть уменьшение объема выборка в два раза приведет к падению мощности минимум в четыре раза. Минимально допустимой мощностью считают 80%, а максимально допустимый уровень ошибки первого рода принимают 5%. Однако всегда следует помнить, что эти границы заданы произвольно и могут изменяться в зависимости от характера и целей исследования. Как правило, научным сообществом признается произвольное изменение мощности, однако в подавляющем большинстве случаев уровень ошибки первого рода не может превышать 5%.

Все сказанное выше имеет непосредственное отношение к этапу планирования исследования. Тем не менее, многие исследователи ошибочно относятся к статистической обработке данных только как к неким манипуляциям, выполняемым после завершения основной части работы. Зачастую после окончания никак не спланированного эксперимента, появляется непреодолимое желание заказать анализ статистических данных на стороне. Но из «кучи мусора» даже специалисту по статистике будет очень сложно выудить ожидаемый исследователем результат. Поэтому при недостаточных знаниях биостатистики необходимо обращаться за помощью в статистическом анализе еще до начала эксперимента.

Обращаясь к самой процедуре анализа, следует указать на два основных типа статистических техник: описательные и доказательные (аналитические). Описательные техники включают в себя методы позволяющие представить данные в компактном и легком для восприятия виде. Сюда можно отнести таблицы, графики, частоты (абсолютные и относительные), меры центральной тенденции (средние, медиана, мода) и меры разброса данных (дисперсия, стандартное отклонение, межквартильный интервал и пр.). Другими словами, описательные методы дают характеристику изучаемым выборкам.

Наиболее популярный (хотя и зачастую ошибочный) способ описания имеющихся количественных данных заключается в определении следующих показателей:

количество наблюдений в выборке или ее объем;
средняя величина(среднее арифметическое);
стандартное отклонение- показатель того, насколько широко изменяются значения переменных.

Важно помнить, что среднее арифметическое и стандартное отклонение — это меры центральной тенденции и разброса в достаточно небольшом числе выборок. В таких выборках значения у большинства объектов с равной вероятностью отклонены от среднего, а их распределение образует симметричный «колокол» (гауссиану или кривую Гаусса-Лапласа). Такое распределение еще называют «нормальным», но в практике медицинского эксперимента оно встречается лишь в 30% случаев. Если же значения переменной распределены несимметрично относительно центра, то группы лучше описывать с помощью медианы и квантилей (процентилей, квартилей, децилей).

Завершив описание групп, необходимо ответить на вопрос об их взаимоотношениях и о возможности обобщить результаты исследования на всю популяцию. Для этого используются доказательные методы биостатистики. Именно о них в первую очередь вспоминают исследователи, когда идет речь о статистической обработке данных. Обычно этот этап работы называют «тестированием статистических гипотез».

Задачи тестирования гипотез можно разделить на две большие группы. Первая группа отвечает на вопрос, имеются ли различия между группами по уровню некоторого показателя, например, различия в уровне печеночных трансаминаз у пациентов с гепатитом и здоровых людей. Вторая группа позволяет доказать наличие связи между двумя или более показателями, например, функции печени и иммунной системы.

В практическом плане задачи из первой группы можно разделить на два подтипа:

сравнение показателя только в двух группах(здоровые и больные, мужчины и женщины);
сравнение трех и более групп(изучение разных доз препарата).

Необходимо учитывать, что статистические методы существенно отличаются для качественных и количественных данных.

В ситуации, когда изучаемая переменная — качественная и сравниваются только две группы, можно использовать критерий «хи-квадрат». Это достаточно мощный и широко известный критерий, однако, он оказывается недостаточно эффективным в случае, если количество наблюдений мало. Для решения данной проблемы существуют несколько методов, такие как поправка Йейтса на непрерывность и точный метод Фишера.

Если изучаемая переменная является количественной, то можно использовать один из двух видов статистических критериев. Критерии первого вида основаны на конкретном типе распределения генеральной совокупности и оперируют параметрами этой совокупности. Такие критерии называют «параметрическими», и они, как правило, базируются на предположении о нормальности распределения значений. Непараметрические критерии не базируются на предположении о типе распределения генеральной совокупности и не используют ее параметры. Иногда такие критерии называют «свободными от распределения» (distribution-free tests). В определенной степени это ошибочно, поскольку любой непараметрический критерий предусматривает, что распределения во всех сравниваемых группах будут одинаковыми, иначе могут быть получены ложноположительные результаты.

Существует два параметрических критерия применяемых к данным, извлеченным из нормально распределенной совокупности: t-тест Стьюдента для сравнения двух групп и F-тест Фишера, позволяющий проверить равенство дисперсий (он же — дисперсионный анализ). Непараметрических же критериев значительно больше. Разные критерии отличаются друг от друга по допущениям, на которых они основаны, по сложности вычислений, по статистической мощности и т. д. Однако наиболее приемлемыми в большинстве случаев считаются критерий Вилкоксона (для связанных групп) и критерий Манна-Уитни, также известный как критерий Вилкоксона для независимых выборок. Эти тесты удобны тем, что не требуют предположения о характере распределения данных. Но если окажется, что выборки взяты из нормально распределенной генеральной совокупности, то их статистическая мощность будет несущественно отличаться от таковой для теста Стьюдента.

Полное описание статистических методов можно найти в специальной литературе, однако, ключевым моментом является то, что каждый статистический тест требует набора правил (допущений) и условий для своего использования, и механический перебор нескольких методов для поиска «нужного» результата абсолютно неприемлем с научной точки зрения. В этом смысле статистические тесты близки к лекарственным препаратам — у каждого есть показания и противопоказания, побочные эффекты и вероятность неэффективности. И столь же опасным является бесконтрольное применение статистических тестов, ведь на них базируются гипотезы и выводы.

Для более полного понимания вопроса точности статистического анализа необходимо определить и разобрать понятие «доверительной вероятности». Доверительная вероятность — это величина, принятая в качестве границы между вероятными и маловероятными событиями. Традиционно, она обозначается буквой «p». Для многих исследователей единственной целью выполнения статистического анализа является расчет заветного значения p, которое словно проставляет запятые в известной фразе «казнить нельзя помиловать». Максимально допустимой доверительной вероятностью считается величина 0,05. Следует помнить, что доверительная вероятность — это не вероятность некоторого события, а вопрос доверия. Выставляя перед началом анализа доверительную вероятность, мы тем самым определяем степень доверия к результатам наших исследований. А, как известно, чрезмерная доверчивость и излишняя подозрительность одинаково негативно сказываются на результатах любой работы.

Уровень доверительной вероятности показывает, какую максимальную вероятность возникновения ошибки первого рода исследователь считает допустимой. Уменьшение уровня доверительной вероятности, иначе говоря, ужесточение условий тестирования гипотез, увеличивает вероятность ошибок второго рода. Следовательно, выбор уровня доверительной вероятности должен осуществляться с учетом возможного ущерба от возникновения ошибок первого и второго рода. Например, принятые в биомедицинской статистике жесткие рамки, определяющие долю ложноположительных результатов не более 5% — это суровая необходимость, ведь на основании результатов медицинских исследований внедряется либо отклоняется новое лечение, а это вопрос жизни многих тысяч людей.

Необходимо иметь в виду, что сама по себе величина p малоинформативна для врача, поскольку говорит только о вероятности ошибочного отклонения нулевой гипотезы. Этот показатель ничего не говорит, например, о размере терапевтического эффекта при применении изучаемого препарата в генеральной совокупности. Поэтому есть мнение, что вместо уровня доверительной вероятности лучше было бы оценивать результаты исследования по величине доверительного интервала. Доверительный интервал — это диапазон значений, в котором с определенной вероятностью заключено истинное популяционное значение (для среднего, медианы или частоты). На практике удобнее иметь оба эти значения, что позволяет с большей уверенностью судить о применимости полученных результатов к популяции в целом.

В заключение следует сказать несколько слов об инструментах, которыми пользуется специалист по статистике, либо исследователь, самостоятельно проводящий анализ данных. Давно ушли в прошлое ручные вычисления. Существующие на сегодняшний день статистические компьютерные программы позволяют проводить статистический анализ, не имея серьезной математической подготовки. Такие мощные системы как SPSS, SAS, R и др. дают возможность исследователю использовать сложные и мощные статистические методы. Однако далеко не всегда это является благом. Не зная о степени применимости используемых статистических тестов к конкретным данным эксперимента, исследователь может провести расчеты и даже получить некоторые числа на выходе, но результат будет весьма сомнительным. Поэтому, обязательным условием для проведения статистической обработки результатов эксперимента должно быть хорошее знание математических основ статистики.

1. номинальную;
2. ординальную;
3. интервальную;
4. рациональную (шкалу отношений).

количество наблюдений в выборке или ее объем;
средняя величина(среднее арифметическое);
стандартное отклонение- показатель того, насколько широко изменяются значения переменных.

В практическом плане задачи из первой группы можно разделить на два подтипа:

сравнение показателя только в двух группах(здоровые и больные, мужчины и женщины);
сравнение трех и более групп(изучение разных доз препарата).

источник