Сравнение плана и факта достаточно частая задача в бизнес-среде.
Рассмотрим различные виды план-факт анализа в Excel и способы их создания.
Наиболее популярными видами сравнения являются таблицы и диаграммы.
Таблицы удобно использовать, если сравнение между планом и фактом происходит по различным показателям, например, данные по продажам различных товаров компании, P&L, CF и т.д.
Диаграммы удобнее для визуализации план-факта конкретного показателя, например, месячная динамика продаж конкретного товара.
Стандартная план-факт таблица состоит из нескольких блоков: в левой части — название показателя, в центре — данные с планом и фактом, в правой — отклонение (в абсолютных величинах, в процентах).
Для лучшей визуализации дополнительно можно окрашивать ячейку или шрифт текста с отклонением, например, в красный и зеленый цвета.
Предположим, что для план-факт графика у нас имеются помесячные данные по продажам (фактические и планируемые), а также отклонение между фактом и планом:
Разберем 2 различных варианта построения план-факт диаграмм.
Выделяем диапазон ячеек A1:M4 и добавляем стандартный график с маркерами (на панели вкладок выбираем Вставка -> График -> График с маркерами):
На графике отобразились 3 ряда — Факт, План и Отклонение, при этом ряд с отклонением получился существенно ниже первых двух за счет эффекта масштаба.
Поэтому сделаем ряд «Отклонение» гистограммой (нажимаем правой кнопкой мыши на ряд, выбираем Изменить тип диаграммы -> Гистограмма -> Гистограмма с группировкой) и перенесем его на вспомогательную ось (снова выбираем ряд, нажимаем правую кнопку и выбираем Формат ряда данных -> Параметры ряда -> По вспомогательной оси)
Теперь приведем в порядок внешний вид план-факт диаграммы — скроем вспомогательную ось, установим минимальные и максимальные значение для основной и вспомогательной оси:
Добавляя подпись данных к рядам получаем окончательный вид план-факт графика:
Еще одним вариантом план-факт анализа является диаграмма с использованием свойств полосы повышения-понижения.
Повторяем действия из первого примера, выделяем диапазон ячеек A1:M3 (без отклонения) и строим график с маркерами:
Во вкладке Конструктор (Excel 2013 и старше) или Макет (Excel 2007-2010) добавляем Полосы повышения-понижения:
Между линией факта и плана появились прямоугольные полосы (полосы повышения-понижения), которые показывают изменение между линиями.
При этом в зависимости от знака отклонения они окрашиваются в разные цвета (в данном примере, если факт больше плана, то в черный и наоборот, если факт меньше плана, то в белый).
Изменим цвет полосы повышения на зеленый, а полосы понижения на красный, а также сделаем их полупрозрачными, чтобы полосы не наезжали на линии графика (нажимаем правой кнопкой мыши на полосу и выбираем Формат полос повышения/понижения):
Подробно ознакомиться с шаблонами диаграмм из разобранных примеров — скачать пример.
источник
Выполним детерминированный факторный анализ на примере модели, описывающей связь финансовых показателей предприятия. Рассмотрим наиболее общий способ цепных подстановок. Для проведения факторного анализа используем надстройку MS EXCEL Variance Analysis Tool от компании Fincontrollex.
Для выполнения детерминированного факторного анализа в среде MS EXCEL сначала кратко напомним читателям о самом методе, затем покажем, как провести факторный анализ самостоятельно на примере простой однопродуктовой модели, и наконец, воспользуемся специализированной надстройкой Variance Analysis Tool для более сложной многопродуктовой модели.
Сначала дадим сухое академическое определение факторного анализа, затем поясним его на примерах.
Детерминированный факторный анализ (ДФА) — это методика исследования влияния факторов на результативный показатель. Предполагается, что связь факторов с результативным показателем носит функциональный характер, которая выражена математической формулой.
Приведем пример такой функциональной связи. В качестве результативного показателя возьмем выручку предприятия, а в качестве факторов, влияющих на выручку – объем продаж, цену реализации изделия и наценку, учитывающая срок оплаты (чем позже покупатель оплатил товар, тем выше наценка). Формула функциональной связи в этом случае выглядит так:
Выручка=(Объем продаж изделия за период)*(Цена изделия)*Наценка
Эта формула является моделью, т.е. разумным упрощением реальности. Действительно, в этой модели есть ряд очевидных допущений:
- предприятие выпускает единственный продукт;
- предполагается, что цена на изделие не меняется в течение периода исследования (на самом деле часто цена зависит от условий поставок различным потребителям);
- у предприятия нет других источников выручки кроме продаж изделия (например, отсутствуют доходы от внереализационных операций);
- под выручкой подразумевается валовая выручка, а не чистая (за вычетом НДС, скидок) и т.д.
Примечание: Детерминированный анализ исключает любую неопределенность и случайность, присутствующие в процессе реальной деятельности предприятия. Хотя результаты такого анализа являются приблизительными, но они помогают исследователю определить степень влияния факторов на результирующий показатель и часто являются отправной точкой для проведения более детального анализа.
Примечание: Представленная выше модель является мультипликативной, т.е. чтобы получить результирующий показатель необходимо перемножить факторы. Также имеются аддитивные (Результат=Фактор1+Фактор2+…), кратные (Результат=Фактор1/Фактор2) и смешанные модели (Результат=Фактор1*Фактор2+Фактор3).
Для проведения ДФА нам понадобятся 2 набора значений факторов и соответствующих им результирующих показателей. Часто в качестве первого набора (называемого базовым) выбирают плановые значения, а в качестве второго – фактические.
Для нашей мультипликативной модели Выручка=Объем*Цена*Наценка заполним следующую таблицу с плановыми и фактическими значениями:
Как видно из таблицы, фактическая выручка существенно меньше плановой. Это произошло из-за того, что фактические значения всех факторов получились меньше запланированных. Необходимо проанализировать, какой фактор внес наибольший вклад в снижение результата: Цена, Наценка или Объем продаж.
В детерминированном факторном анализе используют следующие способы анализа:
- способ цепных подстановок;
- способ абсолютных разниц;
- способ относительных (процентных) разниц;
- интегральный метод и др.
Воспользуемся наиболее универсальным способом цепных подстановок, который может использоваться во всех типах моделей – аддитивных, мультипликативных, кратных и смешанных.
Способ цепных подстановок позволяет выявить, какие факторы повлияли на результирующий показатель наиболее значительно. Этот способ заключается в следующем:
- Сначала изменяют значение одного фактора с планового на фактическое (в нашем случае изменим Объем продаж). При этом другие факторы (Цену и Наценку) нужно оставить неизменными (плановой). Затем вычисляют результирующий показатель (Выручку), а результат сравнивают с имеющимся предыдущим значением (с плановой Выручкой). Далее находят их разность. Чем больше разность по абсолютной величине, тем больше влияние данного фактора на показатель.
- На втором шаге изменяют значения сразу двух факторов на их фактические значения (Объем и Цену), при этом остальные факторы (Наценку) оставляют неизменными (плановыми). Далее вычисляют результирующий показатель (Выручку), и сравнивают его со значением, полученным на предыдущем шаге.
- Далее повторяют замену значений факторов с плановых на фактические до тех пор, пока не будут заменены значения всех факторов модели на фактические.
Все вышесказанное можно записать с помощью простых математических выражений. Сделаем это на примере 3-х факторной мультипликативной модели).
Начинаем с формулы, содержащей только плановые значения факторов:
Результат(План) = Фактор1(План) *Фактор2(План) *Фактор3(План)
Затем для всех факторов по очереди подставляем их фактические значения вместо плановых.
Результат(1)= Фактор1(Факт) *Фактор2(План) *Фактор3(План)
Результат(2)= Фактор1(Факт) *Фактор2(Факт) *Фактор3(План)
Результат(3)= Фактор1(Факт) *Фактор2(Факт) *Фактор3(Факт)
Примечание: Результат(3) = Результат(Факт), т.е. значению результирующего показателя с фактическими значениями всех факторов.
При этом общее изменение Результата будет равно:
Δ Результат = Результат(Факт) – Результат(План)
С другой стороны, общее изменение Результата складывается из суммы изменений результирующего показателя за счет изменения каждого фактора:
Δ Результат = Δ Результат(1) + Δ Результат(2) + Δ Результат(3)
источник
Следующий пример основан на вымышленных данных, относящихся к изучению удовлетворенности жизнью. Предположим, что вопросник был направлен 100 случайно выбранным взрослым. Вопросник содержал 10 пунктов, предназначенных для определения удовлетворенности на работе, удовлетворенности своим хобби, удовлетворенностью домашней жизнью и общей удовлетворенностью в других областях жизни. Ответы на вопросы были введены в компьютер и промасштабированы таким образом, чтобы среднее для всех пунктов стало равным приблизительно 100.
Просто оцените распределение ответа для выполнения имитаций Монте-Карло. Используйте платформу надежности. Настройте распределение выживаемости, чтобы настроить и сравнить различные дистрибутивы. Предотвращение отказов и повышение качества гарантий — все это причины использовать проверенные методы, чтобы в полной мере понять эффективность ваших продуктов в долгосрочной перспективе.
Хотите узнать, как лучше всего распространять информацию о точном прогнозе надежности ваших продуктов и компонентов? Например, анализ распределения выживания позволяет указать непараметрическое распределение и количество параметрических распределений и визуально сравнить настройки.
Результаты были помещены в файл данных Factor.sta. Открыть этот файл можно с помощью опции Файл — Открыть; наиболее вероятно, что этот файл данных находится в директории /Examples/Datasets. Ниже приводится распечатка переменных этого файла (для получения списка выберите Все спецификации переменных в меню Данные).
Цель анализа . Целью анализа является изучение соотношений между удовлетворенностью в различных сферах деятельности. В частности, желательно изучить вопрос о числе факторов, «скрывающихся» за различными областями деятельности и их значимость.
Быстрое определение данных процесса через интерфейс перетаскивания и гибкость генератора карт управления. Создание графических представлений естественных группировок для выделения конфигураций и решения проблем. Платформа анализа измерительной системы поддерживает несколько методов анализа, включая оценку процесса измерения Дональда Дж. Вы можете легко визуализировать источники изменений в ваших измерительных процессах, оценить дефекты продуктов и контролировать стабильность процесса.
Вы предоставляете данные и параметры, необходимые для каждого сканирования, и утилита использует соответствующие макрофункции для вычисления и отображения результатов в таблице. В дополнение к таблицам результатов некоторые инструменты генерируют графики. Функции анализа данных могут использоваться на одном листе за раз. Когда вы анализируете данные на больших электронных таблицах, результаты отображаются на первом листе, а пустые таблицы с форматированием отображаются в других. Чтобы проанализировать данные в других таблицах, повторно запустите инструмент анализа для каждого рабочего листа.
Выбор анализа. Выберите Факторный анализ в меню Анализ — Многомерный разведочный анализ для отображения стартовой панели модуля Факторный анализ. Нажмите на кнопку Переменные на стартовой панели (см. ниже) и выберите все 10 переменных в этом файле.
Используемый инструмент зависит от количества факторов и количества образцов, извлеченных из популяций, подлежащих тестированию. Этот инструмент позволяет провести простой анализ дисперсии данных нескольких образцов. Анализ проверяет гипотезу о том, что каждый образец исходит из одного и того же основного распределения вероятности по отношению к альтернативной гипотезе о том, что лежащие в основе распределения вероятности не одинаковы для всех выборок.
Анова: два фактора с репликацией. Этот инструмент анализа подходит, когда можно классифицировать данные в соответствии с двумя разными размерами. Представьте себе исследование по высоте растений с различными марками удобрений и которые хранятся при разных температурах. Для каждой пары (удобрения, температура) для высоты растений получено равное количество наблюдений.
Другие опции . Для выполнения стандартного факторного анализа в этом диалоговом окне имеется все необходимое. Для получения краткого обзора других команд, доступных из стартовой панели, вы можете выбрать в качестве входного файла корреляционную матрицу (используя поле Файл данных). В поле Удаление ПД вы можете выбрать построчное или попарное исключение или подстановка среднего для пропущенных данных.
Растения, высота которых измеряется для различных марок удобрений, поступают из одного и того же основного населения. Растения, высота которых измеряется с разными уровнями температуры, исходят от одной и той же основной популяции.
- В этом анализе температура не учитывается.
- Маркировка удобрений в этот анализ не включена.
Принимая во внимание влияние различий между отмеченными в первой точке знаками удобрений и различиями температуры, отмеченными во второй точке, шесть образцов, представляющих все пары значений (удобрения, температура), поступают из одной и той же популяции.
Задайте метод выделения факторов. Нажмем теперь кнопку OK для перехода к следующему диалоговому окну с названием Задайте метод выделения факторов. С помощью этого окна диалога вы сможете просмотреть описательные статистики, выполнить множественный регрессионный анализ, выбрать метод выделения факторов, выбрать максимальное число факторов, минимальные собственные значения, а также другие действия, относящиеся к специфике методов выделения факторов. А теперь перейдем во вкладку Описательные.
Альтернативная гипотеза состоит в том, чтобы предположить, что есть эффекты, связанные с определенными парами (удобрениями, температурами) за пределами различий, которые связаны только с удобрением или только с температурой. Анова: два фактора без репликации.
Этот инструмент анализа полезен, когда данные классифицируются в соответствии с двумя различными измерениями, как в случае двухфакторного теста с репликацией. Однако использование этого инструмента предполагает одно наблюдение для каждой пары. Коэффициент корреляции, как и ковариация, позволяет узнать, до какой степени две числовые переменные «меняются вместе».
Просмотр описательных статистик. Теперь нажмите на кнопку Просмотреть корр./средние/ст.откл. в этом окне для того, чтобы открыть окно Просмотр описательных статистик.
Эти два инструмента предоставляют таблицу результатов, матрицу, которая соответственно показывает коэффициент корреляции или ковариацию между каждой парой числовых переменных. Разница между этими двумя инструментами связана с тем, что коэффициенты корреляции находятся в шахматном порядке между -1 и 1 включительно. Ковариации не пошатнулись.
Коэффициент корреляции и ковариация показывают, насколько две переменные «меняются вместе». Средство статистического анализа генерирует одномерный статистический отчет из данных диапазона ввода и предоставляет информацию о центральном тренде и изменчивости данных.
Теперь вы можете рассмотреть описательные статистики графически или с помощью таблиц результатов.
Вычисление корреляционной матрицы. Нажмите на кнопку Корреляции во вкладке Дополнительно для того, чтобы отобразить таблицу результатов с корреляциями.
Инструмент анализа экспоненциального сглаживания. Инструмент анализа экспоненциального сглаживания вычисляет значение, основанное на предсказании, установленном для предыдущего периода. Это значение корректируется в соответствии с ошибкой этого предыдущего прогноза.
Константы сглаживания обычно принимают значения от 0, 2 до 0. Эти значения показывают, что прогноз должен быть скорректирован до 20 или 30 процентов для предыдущей ошибки прогноза. Более высокие константные значения приводят к более быстрым ответам, но могут генерировать противоречивые прогнозы.
Все корреляции в этой таблице результатов положительны, а некоторые корреляции имеют значительную величину. Например, переменные Hobby_1 и Miscel_1 коррелированны на уровне 0.90. Некоторые корреляции (например, корреляции между удовлетворенностью на работе и удовлетворенностью дома) кажутся сравнительно малыми. Это выглядит так, как будто матрица имеет некоторую отчетливую структуру.
Более низкие константы могут привести к значительным задержкам в прогнозируемых значениях. Этот инструмент позволяет проверить нулевую гипотезу о том, что эти два образца взяты из распределений с равными дисперсиями и альтернативной гипотезой о том, что отклонения не равны в базовых дистрибутивах. Инструмент анализа Фурье решает проблемы в линейных системах и анализирует данные с помощью «Быстрого преобразования Фурье» для преобразования данных. Этот инструмент также допускает обратные преобразования, в которых обратный преобразованным данным возвращает исходные данные.
Метод выделения. Теперь нажмем кнопку Отмена в диалоговом окне Просмотр описательных статистик для того, чтобы вернуться в диалоговое окно Задайте метод выделения факторов. Вы можете сделать выбор из нескольких методов выделения во вкладке Дополнительно (см. вкладку Дополнительно диалогового окна Задайте метод выделения факторов для описания каждого метода, а также Вводный обзор с описанием метода Главных компонент и метода Главных факторов). В этом примере по умолчанию принимается метод Главных компонент, поле Макс. число факторов содержит значение 10 (максимальное число факторов в этом примере) и поле Мин. собств. значение содержит 0 (минимальное значение для этой команды).
Анализатор гистограммы вычисляет индивидуальную и кумулятивную частоты для диапазона ячеек данных и местоположений данных. Этот инструмент генерирует данные для ряда вхождений значения в наборе данных. Например, в классе из 20 учеников вы можете определить распределение заметок в алфавитном порядке. Гистограмма показывает терминалы и количество нот между нижней и текущей границами. Наиболее общий одиночный балл представляет собой режим данных.
Средство мобильного усреднения используется для прогнозирования значений за период прогнозирования на основе среднего значения переменной за определенное количество предыдущих периодов. Скользящее среднее обеспечивает информацию о тренде, которая представляет собой простую среднюю маску исторических данных. Используйте этот инструмент для определения прогнозов продаж, например, управления запасами.
Для продолжения анализа нажмите кнопку OK.
Просмотр результатов. Вы можете просмотреть результаты факторного анализа в окне диалога Результаты факторного анализа. Сначала выберите вкладку Объясненная дисперсия.
Генератор случайных чисел. Инструмент анализа генератора случайных чисел завершает серию с независимыми случайными числами, которые поступают из распределения. Вы можете охарактеризовать субъекты популяции с распределением вероятностей. Например, вы можете использовать нормальный закон распределения, чтобы охарактеризовать популяцию отдельных размеров, или использовать распределение Бернулли двух возможных результатов, чтобы охарактеризовать популяцию результатов броска монет.
Средство анализа строки и процентности генерирует таблицу, содержащую ранг каждого значения в наборе данных. Вы можете проанализировать относительный рейтинг значений в наборе данных. Инструмент «Регрессия» выполняет линейный регрессионный анализ, используя метод наименьших квадратов, чтобы найти линию из наблюдаемых значений. Вы можете разделить доли, которые каждый из этих трех факторов представляет в производительности, на основе набора данных о производительности, а затем использовать результаты для прогнозирования эффективности нового спортсмена, который еще не был протестирован, нет теста.
Отображение собственных значений . Назначение собственных значений и их полезность для пользователя при принятии решения о том, сколько следует оставить факторов (интерпретировать) были описаны в Вводном обзоре. Теперь нажмем на кнопку Собственные значения, чтобы получить таблицу с собственными значениями, процентом общей дисперсии, накопленными собственными значениями и накопленными процентами.
Если население слишком велико для обработки или представления графически, вы можете использовать репрезентативную выборку. Вы также можете создать образец, который содержит только значения определенного цикла, если вы считаете, что данные являются периодическими.
Например, если в серии данных содержатся квартальные показатели продаж, создается образец из периодичности, равный четырем местам, для значений в том же квартале в полученной серии. Три инструментария для трех разных предположений: дисперсии населения равны, дисперсии населения не равны, данные двух образцов — данные, наблюдаемые до лечения и после лечения по тем же предметам. Этот тест не предполагает, что дисперсии двух популяций равны. Среди результатов, созданных этим инструментом, является кумулятивная дисперсия, совокупная мера распределения данных по среднему значению, которая получается из следующей формулы.
Как видно из таблицы, собственное значение для первого фактора равно 6.118369; т.е. доля дисперсии, объясненная первым фактором равна приблизительно 61.2%. Заметим, что эти значения случайно оказались здесь легко сравнимыми, так как анализу подвергаются 10 переменных, и поэтому сумма всех собственных значений оказывается равной 10. Второй фактор включает в себя около 18% дисперсии. Остальные факторы содержат не более 5% общей дисперсии. Выбор числа факторов. В разделе Вводный обзор кратко описан способ, как полученные собственные значения можно использовать для решения вопроса о том, сколько факторов следует оставить в модели. В соответствии с критерием Кайзера (Kaiser, 1960), вы должны оставить факторы с собственными значениями большими 1. Из приведенной выше таблицы следует, что критерий приводит к выбору двух факторов.
Для этого теста предполагается, что оба набора данных поступают из распределений с одинаковыми дисперсиями. Мы говорим о гомосексуальном испытании. Для этого теста предполагается, что оба набора данных поступают из распределений с неравными отклонениями. Мы говорим о гетероскедастическом тесте. Используйте этот тест, если объекты двух образцов различны. Используйте сравниваемый образец теста, описанный в следующем примере для группы идентичных субъектов, и если измерения, проведенные для обоих образцов, до и после лечения для каждого испытуемого.
Критерий каменистой осыпи . Теперь нажмите на кнопку График каменистой осыпи, чтобы получить график собственных значений с целью применения критерия осыпи Кэттеля (Cattell, 1966). График, представленный ниже, был дополнен отрезками, соединяющими соседние собственные значения, чтобы сделать критерий более наглядным. Кэттель (Cattell) утверждает, основываясь на методе Монте-Карло, что точка, где непрерывное падение собственных значений замедляется и после которой уровень остальных собственных значений отражает только случайный «шум». На графике, приведенном ниже, эта точка может соответствовать фактору 2 или 3 (как показано стрелками). Поэтому испытайте оба решения и посмотрите, которое из них дает более адекватную картину.
Для вычисления степени свободы используется следующая формула. Этот инструмент используется для проверки нулевой гипотезы о том, что нет никакой разницы между двумя средними населения по отношению к однонаправленной или двунаправленной альтернативной гипотезе. Этот компонент включает инструменты, которые анализируют данные и параметры, а также используя соответствующие статистические или инженерные макрофункции, вычисляет и отображает результаты в выходной таблице.
В дополнение к выходным таблицам некоторые из этих инструментов представляют результаты диаграммы. Функции анализа данных могут использоваться только на листе за один раз. При выполнении анализа данных в группах рабочих листов результаты будут отображаться на первом листе, а на других листах будут отображаться пустые форматированные таблицы. Чтобы проанализировать данные оставшихся листов, снова используйте инструмент анализа для каждого из них.
Теперь рассмотрим факторные нагрузки.
Факторные нагрузки . Как было описано в разделе Вводный обзор, факторные нагрузки можно интерпретировать как корреляции между факторами и переменными. Поэтому они представляют наиболее важную информацию, на которой основывается интерпретация факторов. Сначала посмотрим на (неповернутые) факторные нагрузки для всех десяти факторов. Во вкладке Нагрузки диалогового окна Результаты факторного анализа в поле Вращение факторов зададим значение без вращения и нажмем на кнопку Факторные нагрузки для отображения таблицы нагрузок.
Вспомним, что выделение факторов происходило таким образом, что последующие факторы включали в себя все меньшую и меньшую дисперсию (см. раздел Вводный обзор). Поэтому не удивительно, что первый фактор имеет наивысшую нагрузку. Отметим, что знаки факторных нагрузок имеют значение лишь для того, чтобы показать, что переменные с противоположными нагрузками на один и тот же фактор взаимодействуют с этим фактором противоположным образом. Однако вы можете умножить все нагрузки в столбце на -1 и обратить знаки. Во всем остальном результаты окажутся неизменными.
Вращение факторного решения. Как описано в разделе Вводный обзор, действительная ориентация факторов в факторном пространстве произвольна, и всякое вращение факторов воспроизводит корреляции так же хорошо, как и другие вращения. Следовательно, кажется естественным повернуть факторы таким образом, чтобы выбрать простейшую для интерпретации факторную структуру. Фактически, термин простая структура был придуман и определен Терстоуном (Thurstone, 1947) главным образом для описания условий, когда факторы отмечены высокими нагрузками на некоторые переменные и низкими — для других, а также когда имеются несколько больших перекрестных нагрузок, т.е. имеется несколько переменных с существенными нагрузками на более чем один фактор. Наиболее стандартными вычислительными методами вращения для получения простой структуры является метод вращения варимакс, предложенный Кайзером (Kaiser, 1958). Другими методами, предложенными Харманом (Harman, 1967), являются методы квартимакс, биквартимакс и эквимакс (см. Harman, 1967).
Выбор вращения . Сначала рассмотрим количество факторов, которое вы желаете оставить для вращения и интерпретации. Ранее было решено, что наиболее правдоподобным и приемлемым числом факторов является два, однако на основе критерия осыпи было решено учитывать также и решение с тремя факторами. Нажмите на кнопку Отмена для того, чтобы возвратиться в окно диалога Задайте метод выделения факторов, и измените поле Максимальное число факторов во вкладке Быстрый с 10 на 3, затем нажмите кнопку OK для того, чтобы продолжить анализ.
Теперь выполним вращение по методу варимакс. Во вкладке Нагрузки диалогового окна Результаты факторного анализа в поле Вращение факторов установите значение Варимакс исходных.
Нажмем кнопку Факторные нагрузки для отображения в таблице результатов получаемых факторных нагрузок.
Отображение решения при вращении трех факторов. В таблице приведены существенные нагрузки на первый фактор для всех переменных, кроме относящихся к дому. Фактор 2 имеет довольно значительные нагрузки для всех переменных, кроме переменных связанных с удовлетворенностью на работе. Фактор 3 имеет только одну значительную нагрузку для переменной Home_1. Тот факт, что на третий фактор оказывает высокую нагрузку только одна переменная, наводит на мысль, а не может ли получиться такой же хороший результат без третьего фактора?
Обозрение решения при вращении двух факторов . Снова нажмите на кнопку Отмена в окне диалога Результаты факторного анализа для того, чтобы возвратиться к диалоговому окну Задайте метод выделения факторов. Измените поле Максимальное число факторов во вкладке Быстрый с 3 до 2 и нажмите кнопку OK для того, чтобы перейти в диалоговое окно Результаты факторного анализа. Во вкладке Нагрузки в поле Вращение факторов установите значение Варимакс исходных и нажмите кнопку Факторные нагрузки.
Фактор 1, как видно из таблицы, имеет наивысшие нагрузки для переменных, относящихся к удовлетворенности работой. Наименьшие нагрузки он имеет для переменных, относящихся к удовлетворенности домом. Другие нагрузки принимают промежуточные значения. Фактор 2 имеет наивысшие нагрузки для переменных, связанных с удовлетворенностью дома, низшие нагрузки — для удовлетворенности на работе средние нагрузки для остальных переменных.
Интерпретация решения для двухфакторного вращения . Можно ли интерпретировать данную модель? Все выглядит так, как будто два фактора лучше всего идентифицировать как фактор удовлетворения работой (фактор 1) и как фактор удовлетворения домашней жизнью (фактор 2). Удовлетворение своим хобби и различными другими аспектами жизни кажется относящимися к обоим факторам. Эта модель предполагает в некотором смысле, что удовлетворенность работой и домашней жизнью согласно этой выборке могут быть независимыми друг от друга, но оба дают вклад в удовлетворение хобби и другими сторонами жизни.
Диаграмма решения, основанного на вращении двух факторов . Для получения диаграммы рассеяния двух факторов нажмите на кнопку 2М график нагрузок во вкладке Нагрузки диалогового окна Результаты факторного анализа. Диаграмма, показанная ниже, попросту показывает две нагрузки для каждой переменной. Заметим, что диаграмма рассеяния хорошо иллюстрирует два независимых фактора и 4 переменных (Hobby_1, Hobby_2, Miscel_1, Miscel_2) с перекрестными нагрузками.
Теперь посмотрим, насколько хорошо может быть воспроизведена наблюдаемая ковариационная матрица по двухфакторному решению.
Воспроизведенная и остаточная корреляционная матрица. Нажмите на кнопку Воспроизведенные и остаточные корреляции во вкладке Объясненная дисперсия, для того чтобы получить две таблицы с воспроизведенной корреляционной матрицей и матрицей остаточных корреляций (наблюдаемых минус воспроизведенных корреляций).
Входы в таблице Остаточных корреляций могут быть интерпретированы как «сумма» корреляций, за которые не могут отвечать два полученных фактора. Конечно, диагональные элементы матрицы содержат стандартное отклонение, за которое не могут быть ответственны эти факторы и которые равны квадратному корню из единица минус соответствующие общности для двух факторов (вспомним, что общностью переменной является дисперсия, которая может быть объяснена выбранным числом факторов). Если вы тщательно рассмотрите эту матрицу, то сможете увидеть, что здесь фактически не имеется остаточных корреляций, больших 0.1 или меньшие -0.1 (в действительности только малое количество из них близко к этой величине). Добавим к этому, что первые два фактора включают около 79% общей дисперсии (см. накопленный % собственных значений в таблице результатов).
«Секрет» удачного примера . Пример, который вы только что изучили, на самом деле дает решение двухфакторной задачи, близкое к идеальному. Оно определяет большую часть дисперсии, имеет разумную интерпретацию и воспроизводит корреляционную матрицу с умеренными отклонениями (остаточными корреляциями). На самом деле реальные данные редко позволяют получить такое простое решение, и в действительности это фиктивное множество данных было получено с помощью генератора случайных чисел с нормальным распределением, доступного в системе. Специальным образом в данные были «введены» два ортогональных (независимых) фактора, по которым были сгенерированы корреляции между переменными. Этот пример факторного анализа воспроизводит два фактора такими, как они и были, (т.е. фактор удовлетворенности работой и фактор удовлетворенности домашней жизнью). Таким образом, если бы явление (а не искусственные, как в примере, данные) содержало эти два фактора, то вы, выделив их, могли бы кое-что узнать о скрытой или латентной структуре явления.
Другие результаты . Прежде, чем сделать окончательное заключение, дадим краткие комментарии к другим результатам.
Общности . Для получения общностей решения нажмите на кнопку Общности во вкладке Объясненная дисперсия диалогового окна Результаты факторного анализа. Вспомним, что общность переменной — это доля дисперсии, которая может быть воспроизведена при заданном числе факторов. Вращение факторного пространства не влияет на величину общности. Очень низкие общности для одной или двух переменных (из многих в анализе) могут указывать на то, что эти переменные не очень хорошо объяснены моделью.
Коэффициенты значений. Коэффициенты факторов могут быть использованы для вычисления значений факторов для каждого наблюдения. Сами коэффициенты представляет обычно малый интерес, однако факторные значения полезны при проведении дальнейшего анализа. Для отображения коэффициентов нажмите кнопку Коэффициенты значений факторов во вкладке Значения диалогового окна Результаты факторного анализа.
Значения факторов. Факторные значения могут рассматриваться как текущие значения для каждого опрашиваемого респондента (т.е. для каждого наблюдения исходной таблицы данных). Кнопка Значения факторов во вкладке Значения диалогового окна Результаты факторного анализа позволяет вычислить факторные значения. Эти значения можно сохранить для дальнейшего нажатием кнопки Сохранить значения.
Заключительный комментарий. Факторный анализ — это непростая процедура. Всякий, кто постоянно использует факторный анализ со многими (например, 50 или более) переменными, мог видеть множество примеров «патологического поведения», таких, как: отрицательные собственные значения и не интерпретируемые решения, особые матрицы и т.д. Если вы интересуетесь применением факторного анализа для определения или значащих факторов при большом числе переменных, вам следует тщательно изучить какое-либо подробное руководство (например, книгу Хармана (Harman, 1968)). Таким образом, так как многие критические решения в факторном анализе по своей природе субъективны (число факторов, метод вращения, интерпретация нагрузок), будьте готовы к тому, что требуется некоторый опыт, прежде чем вы почувствуете себя уверенным в нем. Модуль Факторный анализ был разработан специально для того, чтобы сделать легким для пользователя интерактивное переключение между различным числом факторов, вращениями и т.д., так чтобы испытать и сравнить различные решения.
Этот пример взят из справочной системы ППП STATISTICA фирмы StatSoft
Итак, имеем два значения – одно плановое, второе проектное (или базовое и отчетное) и имеем значения отклонения факторов. Задача: построить в Excel красивую диаграмму отображения этих факторов.
Рис.0. Окончательный результат.
Создаем в Excel таблицу, в которой у нас находятся необходимые данные (см.рис.1).
После этого разносим их следующим образом (рис.2)
Теперь подпишем столбцы – столбец I – Значение, далее – Основа, далее Влияние фактора (рис.3).
В качестве базовой диаграммы мы будем использовать либо гистограмму либо линейчатую с наполнением.
Рис.4. Используемые типы диаграмм
Теперь поясню на рис.5 что я имею в виду под основой – это такое значение некоторого ряда которое позволит построить нам диаграмму максимально точно.
В вычислении значений этого ряда поступаем следующим образом:
1. Значение первой основы (сразу после базового значения) принимаем равным либо базовому значению (если первый фактор имеет позитивное влияние) либо (базовое значение – величина влияния) – если фактор имеет негативное влияние.
2. Для последующих основ применяется та же схема. Если значение фактора положительное, то за основу берем результирующее значение, полученное на предыдущем факторе. Если же отрицательное, то берем (результирующее – абсолютное значение негативного фактора).
Что такое основа легко понять по рис.5.
Ту величину, которую я назвал “Влияние фактора” вычисляем как значение изменения фактора по модулю (абсолютное значение) с помощью функции ABS() – рис.6.
Рис.6. Вычисленные значения “Влияния фактора”
Для первой основы используются следующая функция:
ЕСЛИ(L6>0;I5;I5+L6) — т.е. если первый фактор больше нуля, то берем базовое значение, в противном случае берем базовое + значение изменения фактора (в нашем примере получается просто 100).
ЕСЛИ(L7>0;M6;M6+L7) — т.е. если фактор больше нуля, то берем полученное на предыдущем факторе результирующее значение, в противном случае берем базовое + значение изменения фактора.
Ахтунг! Не забывайте про правила сложения – если я говорю “плюс значение”, это значит, что подразумевается не абсолютное значение, а позитивное или негативное. Т.е. для третьего фактора получим следующую логику:
Значение изменения фактора меньше нуля, следовательно берем сумму предыдущего результирующего значения и значения изменения фактора, т.е. основа будет равна 170+(-30)=170-30=140.
Результирующее значение вычисляется по формуле:
ЕСЛИ(L6>0;J6+L6;J6) – т.е. если изменения фактора позитивное, то результирующим значением будет сумма предыдущего результирующего значения и величины изменения фактора, а в противном случае – просто значение основы. Далее переходим уже непосредственно к построению диаграммы. Выделяем ячейки от названия категорий до столбца “Влияние фактора” включительно.
И вставляем необходимый тип диаграммы (в данном случае – гистограмму).
Удаляем вертикальную ось, удаляем основные вертикальные и горизонтальные линии осей и у нас получается нечто вроде рис.9.
В свойствах горизонтальной оси также поставим “Нет линий” (рис.10).
Рис.10. Делаем ось невидимой
Далее добавляем рядам “Влияние фактора” и “Значение” подписи данных. Но получается маленькая нестыковка – даже в тех случаях, когда изменение фактора было отрицательным у нас выводятся положительные значения. Для этого дальше переходим обратно на лист 1 и выставляем соответственные форматы для позитивных и негативных значений.
Для негативных, соответственно: –0,0 – рис.11
Рис.11. Изменение формата чисел в столбце “Влияние фактора”.
Получившийся результат показан на рис.12
Рис.12. Подписи данных после изменения формата
Как видим, уже все изменения отображаются логически верно. Остался маленький штришок – находим точки ряда с негативным изменением и изменяем им цвет заливки на красный, а также меняем цвета подписей данных для этого ряда для большей наглядности (рис.13).
Рис.13. Окончательный результат.
Мы получили симпатичную диаграммку, которую не стыдно вставить в презентацию или в документ.
источник
Чтобы проанализировать изменчивость признака под воздействием контролируемых переменных, применяется дисперсионный метод.
Для изучения связи между значениями – факторный метод. Рассмотрим подробнее аналитические инструменты: факторный, дисперсионный и двухфакторный дисперсионный метод оценки изменчивости.
Условно цель дисперсионного метода можно сформулировать так: вычленить из общей вариативности параметра 3 частные вариативности:
- 1 – определенную действием каждого из изучаемых значений;
- 2 – продиктованную взаимосвязью между исследуемыми значениями;
- 3 – случайную, продиктованную всеми неучтенными обстоятельствами.
В программе Microsoft Excel дисперсионный анализ можно выполнить с помощью инструмента «Анализ данных» (вкладка «Данные» — «Анализ»). Это надстройка табличного процессора. Если надстройка недоступна, нужно открыть «Параметры Excel» и включить настройку для анализа.
Работа начинается с оформления таблицы. Правила:
- В каждом столбце должны быть значения одного исследуемого фактора.
- Столбцы расположить по возрастанию/убыванию величины исследуемого параметра.
Рассмотрим дисперсионный анализ в Excel на примере.
Психолог фирмы проанализировал с помощью специальной методики стратегии поведения сотрудников в конфликтной ситуации. Предполагается, что на поведение влияет уровень образования (1 – среднее, 2 – среднее специальное, 3 – высшее).
Внесем данные в таблицу Excel:
- Открываем диалоговое окно нашего аналитического инструмента. В раскрывшемся списке выбираем «Однофакторный дисперсионный анализ» и нажимаем ОК.
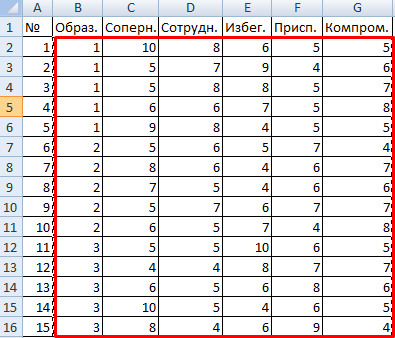
- В поле «Входной интервал» ввести ссылку на диапазон ячеек, содержащихся во всех столбцах таблицы.
- «Группирование» назначить по столбцам.
- «Параметры вывода» — новый рабочий лист. Если нужно указать выходной диапазон на имеющемся листе, то переключатель ставим в положение «Выходной интервал» и ссылаемся на левую верхнюю ячейку диапазона для выводимых данных. Размеры определятся автоматически.
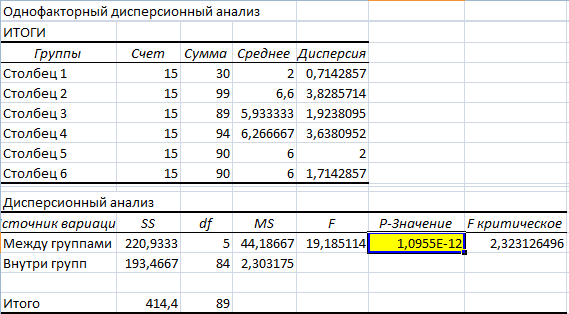
- Результаты анализа выводятся на отдельный лист (в нашем примере).
Значимый параметр залит желтым цветом. Так как Р-Значение между группами больше 1, критерий Фишера нельзя считать значимым. Следовательно, поведение в конфликтной ситуации не зависит от уровня образования.
Факторным называют многомерный анализ взаимосвязей между значениями переменных. С помощью данного метода можно решить важнейшие задачи:
- всесторонне описать измеряемый объект (причем емко, компактно);
- выявить скрытые переменные значения, определяющие наличие линейных статистических корреляций;
- классифицировать переменные (определить взаимосвязи между ними);
- сократить число необходимых переменных.
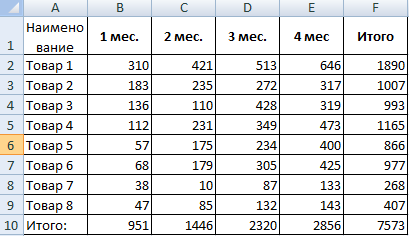
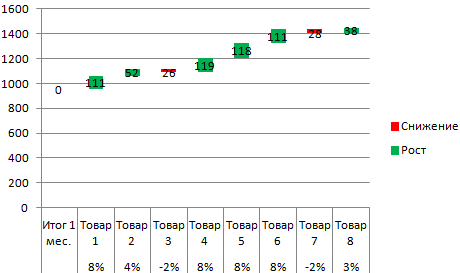
Рассмотрим на примере проведение факторного анализа. Допустим, нам известны продажи каких-либо товаров за последние 4 месяца. Необходимо проанализировать, какие наименования пользуются спросом, а какие нет.
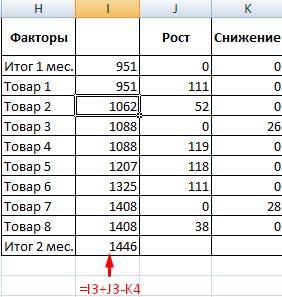
- Посмотрим, за счет, каких наименований произошел основной рост по итогам второго месяца. Если продажи какого-то товара выросли, положительная дельта – в столбец «Рост». Отрицательная – «Снижение». Формула в Excel для «роста»: =ЕСЛИ((C2-B2)>0;C2-B2;0), где С2-В2 – разница между 2 и 1 месяцем. Формула для «снижения»: =ЕСЛИ(J3=0;B2-C2;0), где J3 – ссылка на ячейку слева («Рост»). Во втором столбце – сумма предыдущего значения и предыдущего роста за вычетом текущего снижения.
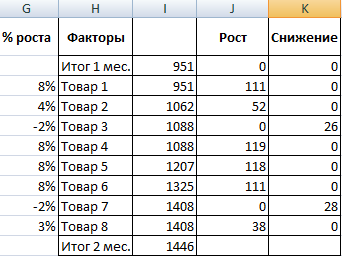
- Рассчитаем процент роста по каждому наименованию товара. Формула: =ЕСЛИ(J3/$I$11=0;-K3/$I$11;J3/$I$11). Где J3/$I$11 – отношение «роста» к итогу за 2 месяц, ;-K3/$I$11 – отношение «снижения» к итогу за 2 месяц.
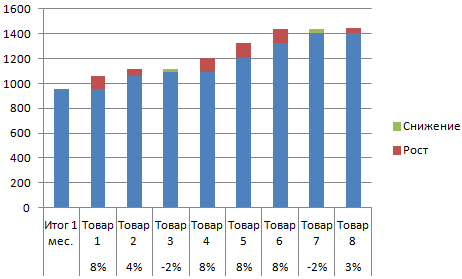
- Выделяем область данных для построения диаграммы. Переходим на вкладку «Вставка» — «Гистограмма».
- Поработаем с подписями и цветами. Уберем накопительный итог через «Формат ряда данных» — «Заливка» («Нет заливки»). С помощью данного инструментария меняем цвет для «снижения» и «роста».
Теперь наглядно видно, продажи какого товара дают основной рост.
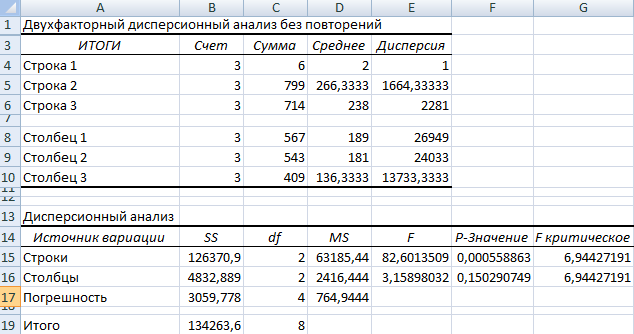
Показывает, как влияет два фактора на изменение значения случайной величины. Рассмотрим двухфакторный дисперсионный анализ в Excel на примере.
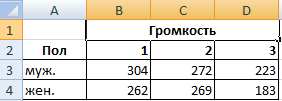
Задача. Группе мужчин и женщин предъявляли звук разной громкости: 1 – 10 дБ, 2 – 30 дБ, 3 – 50 дБ. Время ответа фиксировали в миллисекундах. Необходимо определить, влияет ли пол на реакцию; влияет ли громкость на реакцию.
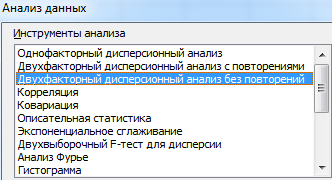
- Переходим на вкладку «Данные» — «Анализ данных» Выбираем из списка «Двухфакторный дисперсионный анализ без повторений».
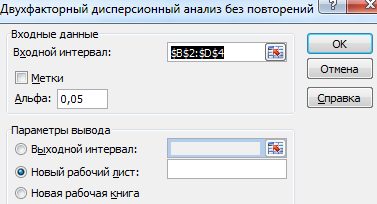
- Заполняем поля. В диапазон должны войти только числовые значения.
- Результат анализа выводится на новый лист (как было задано).
Та как F-статистики (столбец «F») для фактора «Пол» больше критического уровня F-распределения (столбец «F-критическое»), данный фактор имеет влияние на анализируемый параметр (время реакции на звук).
источник
Пакет анализа — это надстройка Excel, которая представляет широкие возможности для проведения статистического анализа. Установка средств Пакет анализа
В стандартной конфигурации программы Excel вы не найдете средства Пакет анализа. Это средство надо установить в качестве надстройки Excel. Для этого выполните следующие действия:
Выберите команду Сервис => Надстройки.
В диалоговом окне Надстройки (рис. 12) установите флажок Пакет анализа.
В результате выполненных действий в нижней части меню Сервис появится новая команда Анализ данных. Эта команда предоставляет доступ к средствам анализа, которые есть в Excel.
Рис. 12. Диалоговое окно Надстройки
Продемонстрируем возможности Пакета программ на следующем примере.
Построим модель объема реализации одного из продуктов фирмы.
Объем реализации — это зависимая переменная Y. В качестве независимых, объясняющих переменных выбраны:
Статистические данные по всем переменным приведены в табл. 5.
В рассматриваемом примере число наблюдений п = 16, факторных признаков т = 5.
Использование инструмента Корреляция
Для проведения корреляционного анализа нужно выполнить следующие действия:
1) расположить данные в смежных диапазонах ячеек;
2) выбрать команду Сервис => Анализ данных (рис. 13). Появится диалоговое окно Анализ данных (рис. 14);
Рис.13. Выбор команды Анализ данных
3)в диалоговом окне Анализ данных выбрать инструмент Корреляция (рис.14), щелкнуть по кнопке ОК. Появится диалоговое окно Корреляция (рис.15);
Рис.14. Выбор команды Анализ данных
4)в диалоговом окне Корреляция в поле «Входной интервал» необходимо ввести диапазон ячеек, содержащих исходные данные. Если также выделены заголовки столбцов, то установить флажок «Метки в первой строке» (рис.15);
5) выбрать параметры вывода. В данном примере — установить переключатель «Новый рабочий лист»;
Рис.15. Диалоговое окно Корреляция
На новом рабочем листе получаем результаты вычислений- таблицу значений коэффициентов парной корреляции(рис.16).
Рис.16. Результаты корреляционного анализа
Анализ матрицы коэффициентов парной корреляции показывает, что зависимая переменная, т.е. объем реализации, имеет тесную связь:
что свидетельствует о наличии коллинеарости. Из этих двух переменных оставим в модели Х5 — индекс расходов. Переменные X1 (время), X3 (цена изделия) и Х4 (цена отрасли) также исключаем из модели, т.к. связь их с результативным признаком Y (объемом реализации) невысокая.
После исключения незначимых факторов имеем п=16,k = 2. Модель приобретает вид:
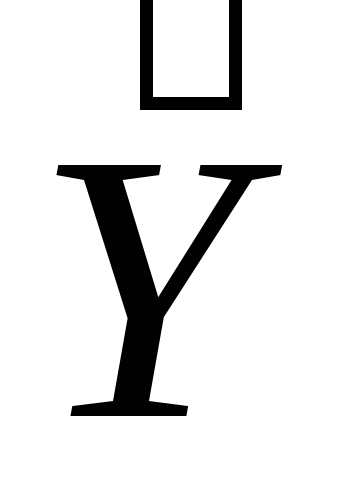
На основе метода наименьших квадратов проведем оценку параметров регрессии по формуле (3). При этом используем данные, приведенные в табл.6.
Непосредственное вычисление (вычисление «вручную») вектора оценок параметров регрессии а согласно формуле (3) весьма громоздко, т.к. матрица независимых переменных X имеет довольно высокую размерность (16 х 3), матрица Y- размерности (16 х 1). В табл. 7 приведены размерности матриц — результатов промежуточных действий.
Задача существенно упрощается при использовании средств Excel. Операции, предписанные формулой (3) целесообразно проводить с помощью следующих встроенных в Excel функций:
•ТРАНСП — транспонирование матриц,
•МОБР — вычисление обратной матрицы.
Для вычисления вектора оценок параметров регрессии а в Excel необходимо выполнить следующие действия:
Выделить диапазон ячеек для записи вектора а, соответствующий его размерности (3×1) (рис. 16).
Используя встроенные в Excel функции, ввести формулу (3), определяющую вектор а.
Нажать одновременно клавиши CTRL + SHIFT + ENTER. Появится результат (рис. 17).
Рис. 16. Выделение диапазона ячеек (3 х 1) для записи вектора оценок параметров регрессии а
Уравнение регрессии зависимости объема реализации от затрат на рекламу и индекса потребительских расходов можно записать в виде:

Рис. 17. Результат вычислений — вектор оценок параметров регрессии а
Расчетные значения Y определяются путем последовательной подстановки в эту модель значений факторов, взятых для каждого момента времени t.
Применение инструмента Регрессия
Для проведения регрессионного анализа с помощью Excel выполните следующие действия:
выберите команду Сервис => Анализ данных;
в диалоговом окне Анализ данных выберите инструмент Регрессия. Щелкните по кнопке ОК;
в диалоговом окне Регрессия в поле «Входной интервал F» введите адрес диапазона ячеек, который представляет зависимую переменную Y. В поле «Входной интервал X» введите адреса одного или нескольких диапазонов, которые содержат значения независимых переменных (в рассматриваемом примере — переменные Х2, Х5). Если выделены заголовки столбцов, то установить флажок «Метки в первой строке»;
выберите параметры вывода. В данном примере – установите переключатель «Новая рабочая книга»;
в поле «Остатки» поставьте необходимые флажки;
Результаты представлены на рис. 18 и заключены в таблицах.
Пояснения к таблице «Регрессионная статистика» (рис. 18)
Наименования в отчете Excel
Коэффициент множественной корреляции, индекс корреляции
Коэффициент детерминации, R 2
Рис. 18. Результаты регрессионного анализа, проведенного с помощью Excel
Пояснения к таблице «Дисперсионный анализ» (рис. 18)
Df — число степеней свободы
Во втором столбце таблицы дисперсионного анализа (рис. 18) содержатся коэффициенты уравнения регрессии а, а1а2, в третьем столбце содержатся стандартные ошибки коэффициентов уравнения регрессии, в четвертом — F-статистика, используемая для проверки значимости коэффициентов уравнения регрессии.
В таблице «Вывод остатка» (рис. 18) приведены вычисленные по модели значения 
Исследование на наличие автокорреляции остатков проведем с помощью d-критерия Дарбина — Уотсона. Для определения величины d-критерия воспользуемся расчетной таблицей 7.
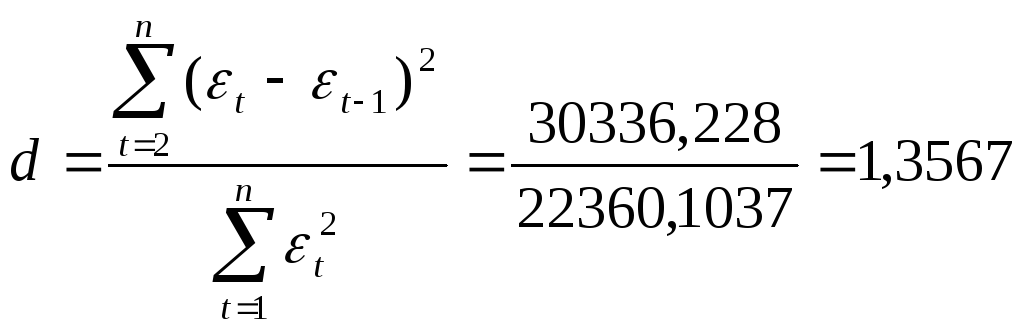
В качестве критических табличных уровней при п = 16, двух объясняющих факторах при уровне значимости = 0,05 возьмем величины вdL = 0,98 и dU=1,54 (приложения А и Б). Расчетное значение d = 1,3567 попало в интервал от dL= 0,98 до dU =1,54 (рис.20)
Рис. 20. Сравнение расчетного значения d-критерия Дарбина -Уотсона с критическими значениями вdL и dU
Так как расчетное значение d-критерия Дарбина-Уотсона попало в зону неопределенности, то нельзя сделать окончательный вывод об автокорреляции остатков по этому критерию.
Для определения степени автокорреляции вычислим коэффициент автокорреляции и проверим его значимость при помощи критерия стандартной ошибки. Стандартная ошибка коэффициента корреляции рассчитывается по формуле:
Коэффициенты автокорреляции случайных данных должны обладать выборочным распределением, приближающимся к нормальному с нулевым математическим ожиданием и средним квадратическим отклонением, равным
Если коэффициент автокорреляции первого порядка r1 находится в интервале
по которой построен прогноз на два шага вперед, причем прогнозные значения на 17-ый и 18-ый периоды соответственно составляют:
Х5(17) = 97,008+1,739*17-0,0488*17 2 = 112,4678,
Описанным выше способом (п. 1.3) построим линию тренда для временного ряда «Расходы на материалы» (рис. 20).
Рис. 20. Результат построения тренда и прогнозирования по тренду для временного ряда «Расходы на рекламу»
Для фактора Х2 «затраты на рекламу» выбираем полиномиальную модель пятой степени (этой модели соответствует наибольшее значение коэффициента детерминации):
Х2= -0,00055157*t 5 + 0,02915029*t 4 — 0,55145744 *t 3 + 4,31897327*t 2 — 11,61564797*t + 12,83076923.
Замечание. Полиномы высоких порядков редко используются при прогнозировании экономических показателей. В этом случае при вычислении прогнозных оценок коэффициентов модели необходимо учитывать большое число знаков после запятой.
Прогнозные значения на 17-ый и 18-ый периоды соответственно составляют:
Для получения прогнозных оценок переменной 7 по модели

подставим в нее найденные прогнозные значения факторов Х2 и Х5, получим:


Доверительный интервал прогноза имеет границы:
верхняя граница прогноза: 
нижняя граница прогноза: 
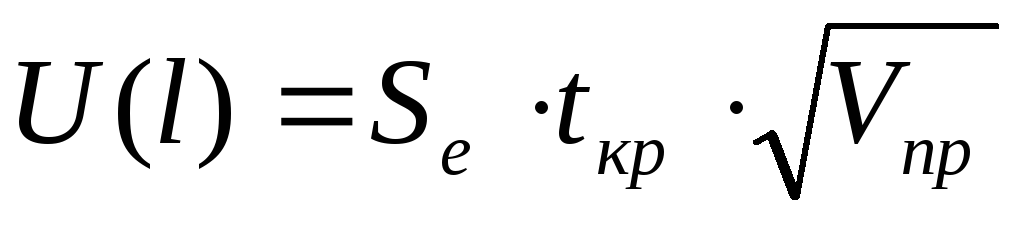

tкр=2,16 (по таблице при =0,05 и числе степеней свободы 13),
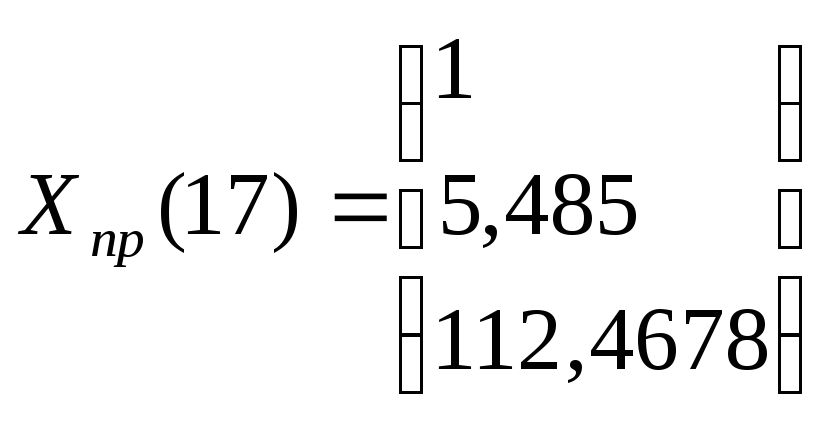
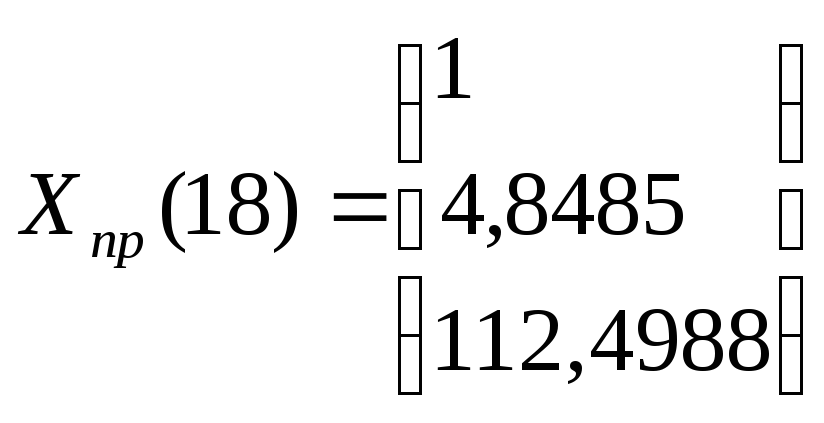
Тогда с использованием Excel , имеем
U(1)=41,473*2,16*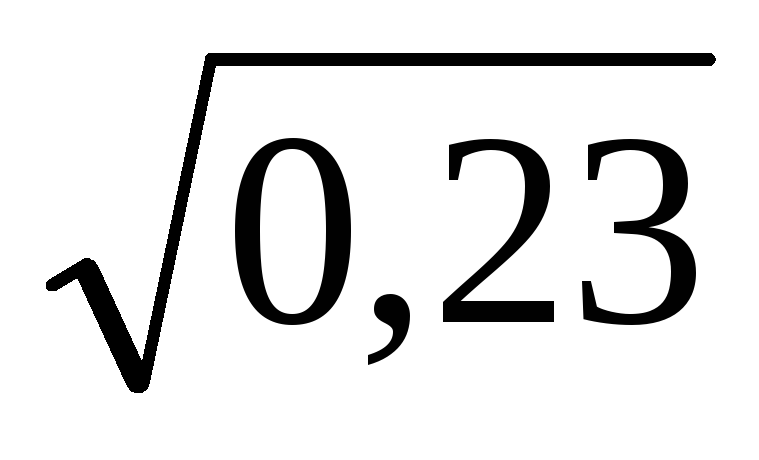
U(2)=41,473*2,16*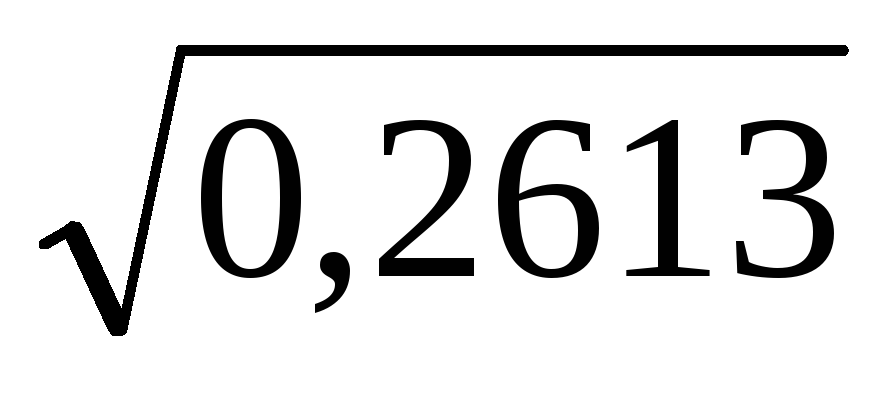
Результаты прогнозных оценок модели регрессии представим в таблице прогнозов (табл. 8).
источник