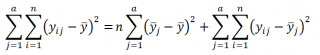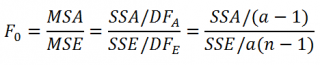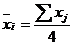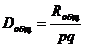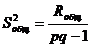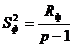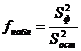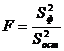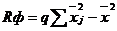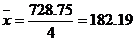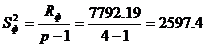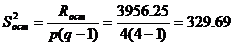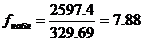Пусть имеется случайная переменная Y, значения которой мы можем измерять. Исследователь предполагает, что эта переменная зависит от фактора, значения которого мы можем контролировать, т.е. задавать с требуемой точностью. Покажем как методом дисперсионного анализа (ANOVA) проверить гипотезу о наличии или отсутствии влияния указанного фактора на зависимую переменную Y.
Disclaimer: Эта статья – о применении MS EXCEL для целей Дисперсионного анализа, поэтому данную статью не стоит рассматривать, как пересказ главы из учебника по статистике. Статья не обладает ни полнотой, ни строгостью изложения положений статистической науки. Теоретические отступления приведены лишь из соображения логики изложения. Использование данной статьи для изучения теории Дисперсионного анализа – плохая идея. Хорошая идея — найти в этой статье формулы MS EXCEL для проведения Дисперсионного анализа.
Перед прочтением этой статьи рекомендуется освежить в памяти следующие понятия статистики:
Дисперсионный анализ (ANOVA, ANalysis Of VAriance) позволяет проверить гипотезу о равенстве нескольких средних значений выборок (взяты ли выборки из одного распределения или из разных распределений).
Примечание: В статье Двухвыборочный t-тест с одинаковыми дисперсиями решалась подобная задача о сравнении средних значений 2-х распределений. Здесь рассмотрим более общую задачу – будем одновременно сравнивать несколько средних значений выборок (более 2-х).
Чтобы пояснить суть дисперсионного анализа приведем пример.
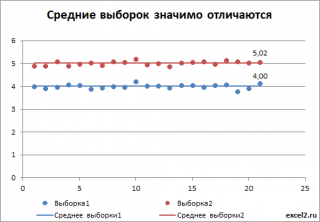
Сгенерируем 2 выборки: первую возьмем из нормального распределения со средним значением равно 4, вторую со средним — 5 (стандартные отклонения одинаковые). Сказать, сильно ли они различаются или нет, невозможно, пока мы не знаем разброс (стандартное отклонение) значений в каждой выборке относительно среднего. Если зададим в распределениях небольшой разброс, скажем 0,1, то в каждой выборке получим близкое к нему значение. В этом случае, очевидно, что наблюдаемое различие между средними равное 1 (5-4=1) – значительное и можно говорить, что выборки взяты из разных распределений (см. картинку ниже).
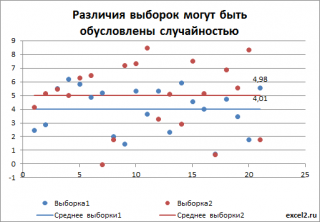
Если же разброс в выборках составляет около 2, то наблюжаемое различие средних значений выборок равное 1 уже не кажется таким значительным.
В дисперсионном анализе эти значения выборок представляют собой значения зависимой переменной Y, а выборки берутся при различных уровнях фактора Х. В первом случае для того дать ответ о зависимости Y от фактора Х, даже не нужно проводить дисперсионный анализ: из диаграммы итак очевидно, что отличие между средними значениями выборок (5-4=1), гораздо больше разброса внутри выборки (0,1). Следовательно, очевидно, что выборки взяты из различных генеральных совокупностей (с различными распределениями), которые соответствуют разным значениям Х.
Во втором случае без дисперсионного анализа не обойтись. Различие между средними значениями может быть обусловлено просто случайностью выборок, взятых из одного распределения.
В конце статьи мы определим математически точно условие «значимости» различия средних выборок.
Примечание: Пользователи, уверенно владеющие методом дисперсионного анализа, могут перейти непосредственно к формулам MS EXCEL.
Пусть необходимо исследовать зависимость некой количественной случайной величины Y от одной переменной, которую мы можем контролировать (устанавливать их значения с требуемой точностью). В теории дисперсионного анализа переменная Y называется зависимой переменной (dependent или response variable), а переменные, от которых исследуется зависимость переменной Y, называются факторами или зависимыми переменными (factors или dependent variables).
Для целей этой статьи будем предполагать, что Y зависит только от одного фактора.
Примечание: Случай зависимости от 2-х факторов рассмотрен в статье Двухфакторный дисперсионный анализ.
Отдельные, заданные значения фактора называются уровнями (levels) или испытаниями (treatments).
Так как мы можем контролировать значения, которые принимает фактор, то данные (набор значений Y), которые получены в результате испытаний, мы назовем экспериментальными, а сам процесс получения этих данных — экспериментом.
Целью эксперимента является исследование влияния различных уровней фактора на переменную Y. В самом деле, так как фактор нами контролируется, то у нас есть возможность сделать несколько наблюдений (измерений) величины Y при определенном заданном уровне фактора. Зачем их делать несколько, ведь значения Y должны получиться одинаковыми? Нет. Так как мы предполагаем, что на переменную Y может влиять множество неконтролируемых нами факторов, то мы будем получать в ходе каждого измерения несколько отличающиеся значения Y. Единственное, что мы можем сделать, это обеспечить одинаковые условия проведения эксперимента для всех измерений.
Например, измеряя расход бензина на 100 км/ч одной и той же марки бензина на одном и том же автомобиле, мы будем получать несколько различные значения. Может непредсказуемо измениться направление ветра, состояние дороги или автомобиля, что в свою очередь повлияет на расход.
Уровни фактора (treatments) будем обозначать буквой j (j изменяется от 1 до a). Каждому уровню фактора соответствует одна выборка (состоит из нескольких измерений). Предполагается, что дисперсии всех выборок σ 2 неизвестны, но равны между собой.
Непосредственно измеренные значения Y при заданном уровне фактора j будем обозначать yij. Количество наблюдений для разных уровней факторов может быть одинаковым или отличаться.
Примечание: Чем больше количество измерений/наблюдений (т.е. размер выборки) мы сделаем, тем более обоснованным будет наш статистический вывод о равенстве средних значений этих выборок.
В тексте статьи будем рассматривать только равные выборки, их размер обозначим n. В Этом случае общее количество измерений N=n*a.
Примечание: В файле примера выполнены вычисления для обоих случаев (равные и неравные по размеру выборки).
Если фактор действительно оказывает влияние на зависимую переменную Y, то при различных уровнях фактора мы должны в среднем получать различные значения Y. Другими словами, мы должны получить «заметно различающиеся» средние выборок при различных уровнях фактора:
Остается выяснить, что значит средние выборок «заметно отличаются».
Общий подход при проведении Дисперсионного анализа: проверить значимость различия средних значений выборок, сравнив один источник разброса (проверяемый фактор) с другим источником разброса (обоснованный лишь случайностью выборок/ случайным воздействием неконтролируемых факторов):
Введя нижеуказанные обозначения, выражение можно записать в компактной форме:
Эти общеупотребительные обозначения расшифровываются следующим образом: SS – это сокращение английского выражения Sum of Squares (сумма квадратов отклонений от среднего), T – это сокращение от Total (Общее среднее), А – это фактор А, E – это сокращение от Error (ошибка).
На основании данных определений, вышеуказанное выражение может быть преобразовано в вычислительную форму:
где, 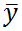
Обратите внимание, что квадраты отклонений имеют размерность дисперсии, т.е. меры изменчивости. Теперь очевидно, что левая часть выражения представляет собой общую изменчивость (разброс) каждого из наблюдений относительно общего среднего. Эта общая изменчивость (SST) состоит из двух частей: SSA — изменчивость, объясненная нашей моделью (междувыборочная изменчивость, основанная на различиях в уровнях фактора) и из SSE — ошибка модели (внутривыборочная изменчивость, сумма разбросов наблюдений внутри каждой выборки).
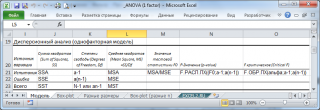
Также в дисперсионном анализе используется понятие среднего квадрата отклонений (Mean Square), т.е. MS. Соответственно для SST имеем MST=SST/(N-1), для SSA имеем MSA=SSA/(n-1), для ошибки модели SSE имеем MSE=SSE/(a(n-1)).
MS имеет смысл средней изменчивости на 1 наблюдение (с некоторой поправкой). Эта поправка отражает тот факт, что MS должна вычисляться не делением SS на соответствующее количество наблюдений, а на число степеней свободы (degrees of freedom, DF). Например, чтобы вычислить MST, мы из N (общего количества наблюдений) должны вычесть 1, т.к. в выражении SST присутствует одно среднее значение (аналогично тому, как мы делали при вычислении дисперсии выборки). Одна степень свободы теряется при вычислении среднего – это видно в формуле выражения для SST.
В SSA мы имеем уже а средних значений (равно количеству уровней фактора, т.е. количеству выборок). Поэтому, из общего количества наблюдений a*n необходимо вычесть а – количество вычисленных средний значений выборок (an-a=a(n-1)).
Напомним, что в дисперсионном анализе проверяется гипотеза о равенстве средних значений этих выборок. Т.е. формулируется нулевая гипотеза Н, которая утверждает, что Y не зависит от фактора и все выборки, измеренные при различных уровнях фактора, на самом деле взяты из одного распределения с общим средним.
Идем дальше. Оказывается, если нулевая справедлива, то:
- случайная величина MSА представляет собой оценку σ 2
- отношение MSА/MSE имеет распределение Фишера с а-1 и a(n-1) степенями свободы.
MSА/MSE обозначают как F (тестовая статистика для однофакторного дисперсионного анализа).
Примечание: Можно показать, что MSE также представляет собой оценку σ 2 дисперсии выборок (математическое ожидание случайной величины MSE равно σ 2 ). Но, в отличие от MSА, MSE представляет собой оценку σ 2 вне зависимости от того, справедлива ли нулевая справедлива или нет.
Теперь, введя основные понятия, рассмотрим вычислительную часть дисперсионного анализа на примере решения задачи.
В качестве задачи рассмотрим технологический процесс изготовления нити в химическом реакторе.
Пусть предполагается, что инженер исследует влияние некой добавки на прочность нити Y. Он решает провести эксперимент:
- Использовать 4 различных концентраций добавки (1%; 5%; 7% и 10%). Прим.: эти значения концентраций не участвуют в расчетах.
- Провести по 6 (n) измерений прочности нити для каждой концентрации добавки.
Таким образом, имеется только 1 фактор (концентрация добавки). Фактор имеет 4 (а=4) различные уровня (j=1; 2; 3; 4). Всего у нас имеется 24 (N=4*6) измерения.
Вроде бы эксперимент полностью описан, теперь инженеру требуется только провести измерения. Однако, есть еще одна сложность: на разброс результатов при различных уровнях фактора может повлиять то, как мы проводим эксперимент.
Представим, что у нас есть только 1 реактор. Инженер включает реактор, делает 6 измерений для первого уровня, затем, для 2-го и т.д. В итоге, может случиться так, что первые 6 измерений у нас будут выполнены в реакторе, который только начал прогреваться, а последние 6, когда он полностью вышел в рабочий режим. Понятно, что такой подход не годится: на разброс выборок может влиять не только концентрация добавки, но и порядок, в котором проводились измерения.
Также не годится подход, когда используются 4 одинаковых, но отдельных реактора для каждого эксперимента: первый реактор для концентрации 1%, второй — для 5% и т.д. Однако, индивидуальные особенности каждого реактора (период эксплуатации, воздействие ремонтов, незначительное различие конструкции допущенное при изготовлении) могут сказаться на разбросе выборки.
То есть для постановки правильного эксперимента требуется исключить влияние конкретного устройства (experimental unit) на значение переменной Y.
Обычно используют полностью рандомизированный эксперимент (completely randomized experimental design) – это когда для каждого испытания (treatment) выбираются образцы экспериментального устройства выбираются случайным способом.
Например, для нашего случая можно предложить следующую схему полностью рандомизированного эксперимента: мы случайным образом выбираем из большого количества одинаковых ректоров (например, из 1000) 6 ректоров для наблюдений первого уровня фактора (для каждого наблюдения 1 реактор), 6 – для второго и т.д. Всего 24 ректора из 1000.
Или можно предложить схему попроще. Всего имеется 24 одинаковых реакторов. Для каждого наблюдения выбираем случайным образом свой реактор.
Или еще проще: каждому из 24 измерений случайным образом (вне зависимости от уровня фактора) назначаем один из 4 одинаковых реакторов. Каждый реактор участвует в 6 измерениях.
Примечание: Т.к. не всегда представляется возможным иметь в распоряжении множество одинаковых экспериментальных устройств для проведения полностью рандомизированного эксперимента, то в статистике часто используются и другие формы проведения экспериментов, например, блочный рандомизированный эксперимент (randomized block design).
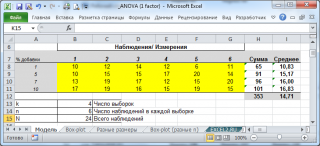
Итак, предположим, что все измерения проведены в соответствии со схемой полностью рандомизированного эксперимента. Результаты измерений представлены в таблице ниже (см. файл примера на листе Модель ).
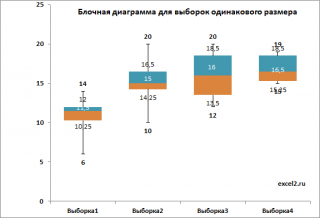
Сначала изучим статистические характеристики набора данных, построив блочную диаграмму.
Из блочной диаграммы видно, что концентрация добавки влияет на прочность нити Y (чем выше концентрация, тем в среднем прочнее нить). Однако, мы пока не можем сделать статистически обоснованный вывод, о том что концентрация добавки влияет на прочность нити. Возможно, различие в средних значениях выборок обусловлено лишь случайностью выборок.
Примечание: Из блочной диаграммы видно, что разброс данных (его отражает дисперсия выборки) имеет примерно одинаковую величину для всех 4-х выборок, что является обязательным условием для корректности применения метода дисперсионного анализа.
Сделаем вспомогательные вычисления по формулам из предыдущего раздела статьи: вычислим средние значения каждой выборки, общее среднее, суммы квадратов SS, степени свободы, MSE, MSA.
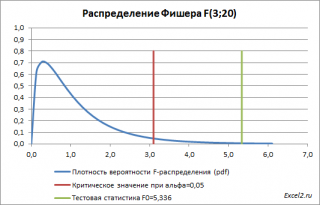
Тестовая статистика вычисляется по формуле:
Т.к. тестовая статистика имеет F-распределение (распределение Фишера), то ее значение, вычисленное на основании наблюдений, должно лежать около среднего значения F-распределения с соответствующими степенями свободы.
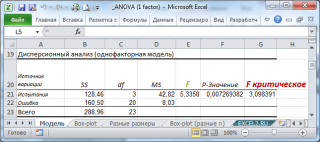
В нашем случае среднее значение F-распределения с 3 и 20 степенями свободы равно 1,11. Если вычисленное нами значение F «значительно» превосходит это значение, то это является маловероятным событием и у нас есть основания для отклонения нулевой гипотезы.
В нашей задаче F равно 5,3358. «Значительно» это или нет? Для ответа на этот вопрос вычислим вероятность этого события (т.е. вероятность события, что случайная величина F, имеющая распределение Фишера с указанными степенями свободы, примет значение 5,3358 или более). Эта вероятность не высока =0,0072. Этого и следовало ожидать, т.к. 5,3358 значительно больше среднего значения 1,11. В MS EXCEL эту вероятность можно вычислить по формуле:
0,0072 – это так называемое p-значение, т.е. вероятность, что статистика F примет вычисленное значение.
Примечание: Обычно под F понимается как сама случайная величина — тестовая статистика F, так и ее конкретное значение F, вычисленное из условий задачи (исходных данных).
Теперь сравним p-значение с уровнем значимости (обычно 0,05 или 0,01). Если p-значение меньше уровня значимости, то нулевую гипотезу отклоняют.
В начале статьи мы задались вопросом о том, как математически точно определить «значимое» отличие средних значений выборок (чтобы мы могли сделать вывод, что уровни фактора влияют на значение переменной Y). Теперь мы можем утверждать, что средние выборок статистически значимо отличаются, если вычисленное p-значение меньше заданного уровня значимости.
Таким образом, наша модель является полезной и наше предположение о зависимости Y (прочности нити) от фактора (концентрации добавки) является статистически обоснованным.
Примечание: Однофакторный дисперсионный анализ можно также выполнить с помощью надстройки Пакет анализа. Об этом см. в статье здесь.
источник
Дисперсионный анализ есть совокупность статистических методов, предназначенных для проверки гипотез о связи между определенными признаками и исследуемыми факторами, которые не имеют количественного описания, а также для установления степени влияния факторов и их взаимодействия. В специальной литературе его часто называют ANOVA (от англоязычного названия Analysis of Variations). Впервые этот метод был разработан Р. Фишером в 1925 г.
Этот метод используется для исследования связи между качественными (номинальными) признаками и количественной (непрерывной) переменной. По сути, он осуществляет тестирование гипотезы о равенстве средних арифметических нескольких выборок. Таким образом, его можно рассматривать как параметрический критерий для сравнения центров сразу нескольких выборок. Если использовать этот метод для двух выборок, то результаты дисперсионного анализа будут идентичны результатам t-критерия Стьюдента. Однако, в отличие от других критериев, это исследование позволяет изучить проблему более детально.
Дисперсионный анализ в статистике базируется на законе: сумма квадратов отклонений объединенной выборки равна сумме квадратов внутригрупповых отклонений и сумме квадратов межгрупповых отклонений. Для исследования используется критерий Фишера для установления значимости различия межгрупповых дисперсий от внутригрупповых. Однако для этого необходимыми предпосылками являются нормальность распределения и гомоскедастичность (равенство дисперсий) выборок. Различают одномерный (однофакторный) дисперсионный анализ и многомерный (многофакторный). Первый рассматривает зависимость исследуемой величины от одного признака, второй — сразу от многих, а также позволяет выявить связь между ними.
Факторами называют контролируемые обстоятельства, что влияют на конечный результат. Его уровнем или способом обработки называют значение, которое характеризует конкретное проявление этого условия. Эти цифры обычно подают в номинальной или порядковой шкале измерений. Часто выходные значения измеряют в количественных или порядковых шкалах. Тогда возникает проблема группировки выходных данных в ряде наблюдений, что соответствуют примерно одинаковым числовым значениям. Если количество групп взять чрезмерно большим, то количество наблюдений в них может оказаться недостаточным для получения надежных результатов. Если брать число чрезмерно малым, это может привести к потере существенных особенностей влияния на систему. Конкретный способ группировки данных зависит от объема и характера варьирования значений. Количество и размеры интервалов при однофакторном анализе чаще всего определяют по принципу равных промежутков или по принципу равных частот.
Итак, существуют случаи, когда нужно сравнить две или больше выборок. Именно тогда и целесообразно применение дисперсионного анализа. Название метода указывает на то, что выводы делают на основе исследования составляющих дисперсии. Суть изучения состоит в том, что общее изменение показателя разбивают на составляющие части, которые соответствуют действию каждого отдельно взятого фактора. Рассмотрим ряд задач, которые решает типичный дисперсионный анализ.
В цехе есть ряд станков — автоматов, которые изготавливают определенную деталь. Размер каждой детали — это случайная величина, которая зависит от настройки каждого станка и случайных отклонений, возникающих в процессе изготовления деталей. Нужно по данным измерений размеров деталей определить, одинаково ли настроены станки.
Во время изготовления электрического аппарата используют различные типы изоляционной бумаги: конденсаторную, электротехническую и др. Аппарат можно пропитать различными веществами: эпоксидной смолой, лаком, смолой МЛ-2 и др. Утечки можно устранять под вакуумом при повышенном давлении, при нагреве. Пропитывать можно методом погружения в лак, под непрерывной струей лака и т. п. Электрический аппарат в целом заливают определенным компаундом, вариантов которого есть несколько. Показателями качества являются электрическая прочность изоляции, температура перегрева обмотки в рабочем режиме и ряд других. Во время отработки технологического процесса изготовления аппаратов надо определить, как влияет каждый из перечисленных факторов на показатели аппарата.
Троллейбусное депо обслуживает несколько троллейбусных маршрутов. На них работают троллейбусы различных типов, и оплату за проезд собирают 125 контролеров. Руководство депо интересует вопрос: как сравнить экономические показатели работы каждого контролера (выручку) учитывая различные маршруты, различные типы троллейбусов? Как определить экономическую целесообразность выпуска троллейбусов определенного типа на тот или другой маршрут? Как установить обоснованные требования к величине выручки, которую приносит кондуктор, на каждом маршруте в различных типах троллейбусов?
Задача по выбору метода состоит в том, как получить максимум информации относительно влияния на конечный результат каждого фактора, определить числовые характеристики такого влияния, их надежность при минимальных затратах и за максимально короткое время. Решить такие задачи позволяют методы дисперсионного анализа.
Исследование своей целью ставит оценку величины влияния конкретного случая на анализируемый отзыв. Другой задачей однофакторного анализа может быть сравнение двух или нескольких обстоятельств друг с другом с целью определения разницы их влияния на отзыв. Если нулевую гипотезу отвергают, то следующим этапом будет количественное оценивание и построение доверительных интервалов для полученных характеристик. В случае, когда нулевая гипотеза не может быть отброшенной, обычно ее принимают и делают вывод о сущности влияния.
Однофакторный дисперсионный анализ может стать непараметрическим аналогом рангового метода Краскела-Уоллиса. Он разработан американскими математиком Уильямом Краскелом и экономистом Вильсоном Уоллисом в 1952 г. Этот критерий назначен для проверки нулевой гипотезы о равенстве эффектов влияния на исследуемые выборки с неизвестными, но равными средними величинами. При этом количество выборок должно быть больше двух.
Критерий Джонкхиера (Джонкхиера-Терпстра) был предложен независимо друг от друга нидерландским математиком Т. Дж. Терпстром в 1952 г. и британским психологом Е. Р. Джонкхиером в 1954 г. Его применяют тогда, когда заранее известно, что имеющиеся группы результатов упорядочены по росту влияния исследуемого фактора, который измеряют в порядковой шкале.
М — критерий Бартлетта, предложенный британским статистиком Маурисом Стивенсоном Бартлеттом в 1937 г., применяют для проверки нулевой гипотезы о равенстве дисперсий нескольких нормальных генеральных совокупностей, с которых взяты исследуемые выборки, в общем случае имеющие различные объемы (число каждой выборки должно быть не меньше четырех).
G — критерий Кохрена, который открыл американец Вильям Геммел Кохрен в 1941 г. Его используют для проверки нулевой гипотезы о равенстве дисперсий нормальных генеральных совокупностей по независимым выборкам равного объема.
Непараметрический критерий Левене, предложенный американским математиком Ховардом Левене в 1960 г., является альтернативой критерия Бартлетта в условиях, когда нет уверенности в том, что исследуемые выборки подчиняются нормальному распределению.
В 1974 г. американские статистики Мортон Б. Браун и Алан Б. Форсайт предложили тест (критерий Брауна-Форсайта), который несколько отличается от критерия Левене.
Двухфакторный дисперсионный анализ применяют для связанных нормально распределенных выборок. На практике часто используют и сложные таблицы этого метода, в частности те, в которых каждая ячейка содержит набор данных (повторные измерения), соответствующих фиксированным значениям уровней. Если предположения, необходимые для применения двухфакторного дисперсионного анализа, не выполняются, то используют непараметрический ранговый критерий Фридмана (Фридмана, Кендалла и Смита), разработанный американским экономистом Милтоном Фридманом в конце 1930 г. Этот критерий не зависит от типа распределения.
Предполагается только, что распределение величин является одинаковым и непрерывным, а сами они независимы одна от другой. При проверке нулевой гипотезы выходные данные подают в форме прямоугольной матрицы, в которой строки соответствуют уровням фактора В, а столбцы — уровням А. Каждая ячейка таблицы (блока) может быть результатом измерений параметров на одном объекте или на группе объектов при постоянных значениях уровней обоих факторов. В этом случае соответствующие данные подают как средние значения определенного параметра по всем измерениям или объектам исследуемой выборки. Для применения критерия выходных данных необходимо перейти от непосредственных результатов измерений к их рангу. Ранжирование осуществляют по каждой строке отдельно, то есть величины упорядочивают для каждого фиксированного значения.
Критерий Пейджа (L-критерий), предложенный американским статистиком Е. Б. Пейджем в 1963 г., предназначен для проверки нулевой гипотезы. Для больших выборок применяют аппроксимацию Пейджа. Они при условии реальности соответствующих нулевых гипотез подчиняются стандартному нормальному распределению. В случае, когда в строках исходной таблицы есть одинаковые значения, необходимо использовать средние ранги. При этом точность выводов будет тем хуже, чем больше будет количеств таких совпадений.
Q — критерий Кохрена, предложенный В. Кохреном в 1937 г. Его используют в случаях, когда группы однородных субъектов подвергаются воздействиям, количество которых превышает два и для которых возможны два варианта отзывов — условно-отрицательный (0) и условно-положительный (1). Нулевая гипотеза состоит из равенства эффектов влияния. Двухфакторный дисперсионный анализ дает возможность определить существование эффектов обработки, однако не дает возможности установить, для каких именно столбцов существует этот эффект. При решении данной проблемы применяют метод множественных уравнений Шеффе для связанных выборок.
Задача многофакторного дисперсионного анализа возникает тогда, когда нужно определить влияние двух или большего количества условий на определенную случайную величину. Исследование предусматривает наличие одной зависимой случайной величины, измеренной в шкале разницы или отношений, и нескольких независимых величин, каждая из которых выражена в шкале наименований или в ранговой. Дисперсионный анализ данных является достаточно развитым разделом математической статистики, который имеет массу вариантов. Концепция исследования общая как для однофакторного, так и для многофакторного. Сущность ее состоит в том, что общую дисперсию разбивают на составляющие, что соответствует определенной группировке данных. Каждой группировке данных соответствует своя модель. Здесь мы рассмотрим только основные положения, нужные для понимания и практического использования наиболее применяемых его вариантов.
Дисперсионный анализ факторов требует достаточно внимательного отношения к сбору и подаче входных данных, а особенно к интерпретации результатов. В отличие от однофакторного, результаты которого можно условно разместить в определенной последовательности, результаты двухфакторного требуют более сложного представления. Еще сложнее ситуация возникает, когда есть три, четыре или больше обстоятельств. Из-за этого в модель достаточно редко включают больше трех (четырех) условий. Примером может быть возникновение резонанса при определенной величине емкости и индуктивности электрического круга; проявление химической реакции при определенной совокупности элементов, из которых построена система; возникновение аномальных эффектов в сложных системах при определенном совпадении обстоятельств. Наличие взаимодействия может в корне изменить модель системы и иногда привести к переосмыслению природы явлений, с которыми имеет дело экспериментатор.
Данные измерений достаточно часто можно группировать не по двум, а по большему количеству факторов. Так, если рассматривать дисперсионный анализ срока службы покрышек колес троллейбуса с учетом обстоятельств (завод-производитель и маршрут, на котором эксплуатируются покрышки), то можно выделить как отдельное условие сезон, во время которого эксплуатируются покрышки (а именно: зимняя и летняя эксплуатация). В результате будем иметь задачу трехфакторного метода.
При наличии большего количества условий подход такой же, как и в двухфакторном анализе. Во всех случаях модель пытаются упростить. Явление взаимодействия двух факторов проявляется не так часто, а тройное взаимодействие бывает только в исключительных случаях. Включают то взаимодействие, для которого есть предыдущая информация и серьезные основания, чтобы ее учесть в модели. Процесс выделения отдельных факторов и их учета относительно простой. Поэтому часто возникает желание выделить больше обстоятельств. Этим не следует увлекаться. Чем больше условий, тем менее надежной становится модель и тем больше вероятность ошибки. Сама модель, в которую входит большое количество независимых переменных, становится достаточно сложной для интерпретации и неудобной для практического использования.
Дисперсионный анализ в статистике — это метод получения результатов наблюдений, зависимых от различных одновременно действующих обстоятельств, и оценки их влияния. Управляемую переменную величину, которая соответствует способу воздействия на объект исследования и в некоторый период времени приобретает определенное значение, называют фактором. Они могут быть качественными и количественными. Уровни количественных условий приобретают определенное значение на числовой шкале. Примерами являются температура, давление прессования, количество вещества. Качественные факторы — это разные вещества, разные технологические способы, аппараты, наполнители. Их уровням соответствует шкала наименований.
К качественным можно отнести также вид упаковочного материала, условия хранения лекарственной формы. Сюда же рационально отнести степень измельчения сырья, фракционный состав гранул, имеющих количественное значение, однако плохо поддающихся регулированию, если использовать количественную шкалу. Число качественных факторов зависит от вида лекарственной формы, а также физических и технологических свойств лекарственных веществ. Например, из кристаллических веществ можно получать таблетки прямым прессованием. В этом случае достаточно провести выбор скользящих и смазывающих веществ.
- Настойки. Состав экстрагента, тип экстрактора, способ подготовки сырья, способ получения, способ фильтрации.
- Экстракты (жидкие, густые, сухие). Состав экстрагента, способ экстракции, тип установки, способ удаления экстрагента и балластных веществ.
- Таблетки. Состав вспомогательных веществ, наполнители, разрыхлители, связующие, смазывающие и скользящие вещества. Способ получения таблеток, вид технологического оборудования. Вид оболочки и ее компонентов, пленкообразователи, пигменты, красители, пластификаторы, растворители.
- Инъекционные растворы. Вид растворителя, способ фильтрации, природа стабилизаторов и консервантов, условия стерилизации, способ заполнения ампул.
- Суппозитории. Состав суппозиторной основы, способ получения суппозиториев, наполнителей, упаковки.
- Мази. Состав основы, структурные компоненты, способ приготовления мази, вид оборудования, упаковка.
- Капсулы. Вид оболочечного материала, способ получения капсул, тип пластификатора, консерванта, красителя.
- Линименты. Способ получения, состав, тип оборудования, тип эмульгатора.
- Суспензии. Вид растворителя, вид стабилизатора, метод диспергирования.
- Разрыхлитель. Крахмал картофельный, глина белая, смесь натрия гидрокарбоната с кислотой лимонной, магния карбонат основной.
- Связывающий раствор. Вода, крахмальный клейстер, сахарный сироп, раствор метилцеллюлозы, раствор оксипропилметилцеллюлозы, раствор поливинилпирролидона, раствор поливинилового спирта.
- Скользящая вещество. Аэросил, крахмал, тальк.
- Наполнитель. Сахар, глюкоза, лактоза, натрия хлорид, фосфат кальция.
- Смазывающее вещество. Стеариновая кислота, полиэтиленгликоль, парафин.
Одним из важнейших критериев оценки состояния государства, по которым проводится оценка уровня его благосостояния и социально-экономического развития, является конкурентоспособность, то есть совокупность свойств, присущих национальной экономике, которые определяют способность государства конкурировать с другими странами. Определив место и роль государства на мировом рынке, можно установить четкую стратегию обеспечения экономической безопасности в международных масштабах, ведь она является залогом положительных взаимоотношений России со всеми игроками мирового рынка: инвесторами, кредиторами, правительствами государств.
Для сравнения уровня конкурентоспособности государств проводится ранжирование стран с помощью комплексных индексов, которые включают различные взвешенные показатели. В основу этих индексов заложены ключевые факторы, влияющие на экономическое, политическое и т. п. положение. Комплекс моделей исследования конкурентоспособности государства предусматривает использование методов многомерного статистического анализа (в частности, это дисперсионный анализ (статистика), эконометрическое моделирование, принятие решений) и включает следующие основные этапы:
- Формирование системы показателей-индикаторов.
- Оценку и прогнозирование индикаторов конкурентоспособности государства.
- Сравнение показателей-индикаторов конкурентоспособности государств.
А теперь рассмотрим содержание моделей каждого из этапов данного комплекса.
На первом этапе с помощью методов экспертного изучения формируется обоснованный комплекс экономических показателей-индикаторов оценки конкурентоспособности государства с учетом специфики ее развития на основе международных рейтингов и данных статистических отделов, отражающих состояние системы в целом и ее процессов. Выбор этих показателей обоснован необходимостью отобрать те из них, которые наиболее полно с точки зрения практики позволяют определить уровень государства, его инвестиционную привлекательность и возможности относительной локализации существующих потенциальных и реально действующих угроз.
Основные показатели-индикаторы международных рейтинг-систем — это индексы:
- Глобальной конкурентоспособности (ИГК).
- Экономической свободы (ИЭС).
- Развития человеческого потенциала (ИРЧП).
- Восприятия коррупции (ИВК).
- Внутренних и внешних угроз (ИВЗЗ).
- Потенциала международного влияния (ИПМВ).
Второй этап предусматривает оценку и прогнозирование индикаторов конкурентоспособности государства по международным рейтингам для исследуемых 139 государств мира.
Третий этап предусматривает сравнение условий конкурентоспособности государств при помощи методов корреляционно-регрессионного анализа.
Используя результаты исследования можно определить характер протекания процессов в целом и по отдельным составляющим конкурентоспособности государства; проверить гипотезу о влиянии факторов и их взаимосвязи при соответствующем уровне значимости.
Реализация предложенного комплекса моделей позволит не только оценить сложившуюся ситуацию уровня конкурентоспособности и инвестиционной привлекательности государств, но и проанализировать недостатки управления, предупредить ошибки неправильных решений, не допустить развития кризиса в государстве.
источник
Назначение сервиса . С помощью данного онлайн-калькулятора можно:
- провести однофакторный дисперсионный анализ;
- ответить на вопрос — совпадают или нет средние значения экспериментов;
- при выбранном уровне значимости подтвердить или опровергнуть нулевую гипотезу H о равенстве групповых средних;
- Решение онлайн
- Видеоинструкция
Пример . Изделие железнодорожного транспорта с целью испытания на надежность эксплуатируется q раз, i=1. q на p уровнях времени работы Tj , j=1. p. В каждом испытании подсчитываются числа отказов nij. На уровне значимости α = 0,05 исследовать влияние времени работы изделия на число появления отказов методом однофакторного дисперсионного анализа при q=4 , p=4 . Результаты испытаний nij представлены в таблицах.
Решение.
Процедура однофакторного дисперсионного анализа. Находим групповые средние:
| N | П1 | П2 | П3 | П4 |
| 1 | 145 | 210 | 195 | 155 |
| 2 | 140 | 200 | 190 | 150 |
| 3 | 150 | 190 | 240 | 180 |
| 4 | 190 | 195 | 210 | 175 |
| x | 156.25 | 198.75 | 208.75 | 165 |
Обозначим р — количество уровней фактора (р=4). Число измерений на каждом уровне одинаково и равно q=4.
В последней строке помещены групповые средние для каждого уровня фактора.
Общую среднюю можно получить как среднее арифметическое групповых средних: 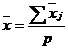
На разброс групповых средних процента отказа относительно общей средней влияют как изменения уровня рассматриваемого фактора, так и случайные факторы.
Для того чтобы учесть влияние данного фактора, общая выборочная дисперсия разбивается на две части, первая из которых называется факторной S 2 ф, а вторая — остаточной S 2 ост.
С целью учета этих составляющих вначале рассчитывается общая сумма квадратов отклонений вариант от общей средней:
Rобщ = ∑∑(xij— x ) (2)
и факторная сумма квадратов отклонений групповых средних от общей средней, которая и характеризует влияние данного фактора:
Rф = q·( x ij— x )
Последнее выражение получено путем замены каждой варианты в выражении Rобщ групповой средней для данного фактора.
Остаточная сумма квадратов отклонений получается как разность:
Rост = Rобщ — Rф
Для определения общей выборочной дисперсии необходимо Rобщ разделить на число измерений pq:
а для получения несмещенной общей выборочной дисперсии это выражение нужно умножить на pq/(pq-1):
Соответственно, для несмещенной факторной выборочной дисперсии:
где p-1 — число степеней свободы несмещенной факторной выборочной дисперсии.
С целью оценки влияния фактора на изменения рассматриваемого параметра рассчитывается величина:
Так как отношение двух выборочных дисперсий S 2 ф и S 2 ост распределено по закону Фишера-Снедекора, то полученное значение fнабл сравнивают со значением функции распределения
в критической точке fкр, соответствующей выбранному уровню значимости a.
Если fнабл>fкр, то фактор оказывает существенное воздействие и его следует учитывать, в противном случае он оказывает незначительное влияние, которым можно пренебречь.
Для расчета Rнабл и Rф могут быть использованы также формулы: 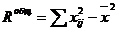
Находим общую среднюю по формуле (1):
Для расчета Rобщ по формуле (4) составляем таблицу 2 квадратов вариант:
| N | П 2 1 | П 2 2 | П 2 3 | П 2 4 |
| 1 | 21025 | 44100 | 38025 | 24025 |
| 2 | 19600 | 40000 | 36100 | 22500 |
| 3 | 22500 | 36100 | 57600 | 32400 |
| 4 | 36100 | 38025 | 44100 | 30625 |
| ∑ | 99225 | 158225 | 175825 | 109550 |
Общая средняя вычисляется по формуле (1):
Rобщ = 99225 + 158225 + 175825 + 109550 — 4 • 4 • 182.19 2 = 11748.44
Находим Rф по формуле (5):
Rф = 4(156.25 2 + 198.75 2 + 208.75 2 + 165 2 ) — 4 • 182.19 2 = 7792.19
Получаем Rост: Rост = Rобщ — Rф = 11748.44 — 7792.19 = 3956.25
Определяем факторную и остаточную дисперсии:
Если средние значения случайной величины, вычисленные по отдельным выборкам одинаковы, то оценки факторной и остаточной дисперсий являются несмещенными оценками генеральной дисперсии и различаются несущественно.
Тогда сопоставление оценок этих дисперсий по критерию Фишера должно показать, что нулевую гипотезу о равенстве факторной и остаточной дисперсий отвергнуть нет оснований.
Оценка факторной дисперсии больше оценки остаточной дисперсии, поэтому можно сразу утверждать не справедливость нулевой гипотезы о равенстве математических ожиданий по слоям выборки.
Иначе говоря, в данном примере фактор Ф оказывает существенное влияния на случайную величину.
Проверим нулевую гипотезу H: равенство средних значений х .
Находим fнабл
Для уровня значимости α=0.05, чисел степеней свободы 3 и 12 находим fкр из таблицы распределения Фишера-Снедекора.
fкр(0.05; 3; 12) = 3.49
В связи с тем, что fнабл > fкр, нулевую гипотезу о существенном влиянии фактора на результаты экспериментов принимаем.
Пример №2 . Студентов 1-го курса опрашивали с целью выявления занятий, которым они посвящают свое свободное время. Проверьте, различаются ли распределение вербальных и невербальных предпочтений студентов.
Находим групповые средние:
| N | П1 | П2 |
| 1 | 12 | 17 |
| 2 | 18 | 19 |
| 3 | 23 | 25 |
| 4 | 10 | 7 |
| 5 | 15 | 17 |
| x | 15.6 | 17 |
Обозначим р — количество уровней фактора (р=2). Число измерений на каждом уровне одинаково и равно q=5.
В последней строке помещены групповые средние для каждого уровня фактора.
Общую среднюю можно получить как среднее арифметическое групповых средних: 
На разброс групповых средних процента отказа относительно общей средней влияют как изменения уровня рассматриваемого фактора, так и случайные факторы.
Для того чтобы учесть влияние данного фактора, общая выборочная дисперсия разбивается на две части, первая из которых называется факторной S 2 ф, а вторая — остаточной S 2 ост.
С целью учета этих составляющих вначале рассчитывается общая сумма квадратов отклонений вариант от общей средней:
Rобщ=∑∑(xij— x )
и факторная сумма квадратов отклонений групповых средних от общей средней, которая и характеризует влияние данного фактора:
Rф=q∑( x ij— x )
Последнее выражение получено путем замены каждой варианты в выражении Rобщ групповой средней для данного фактора.
Остаточная сумма квадратов отклонений получается как разность:
Rост = Rобщ — Rф
Для определения общей выборочной дисперсии необходимо Rобщ разделить на число измерений pq:
а для получения несмещенной общей выборочной дисперсии это выражение нужно умножить на pq/(pq-1):
Соответственно, для несмещенной факторной выборочной дисперсии:
где p-1 — число степеней свободы несмещенной факторной выборочной дисперсии.
С целью оценки влияния фактора на изменения рассматриваемого параметра рассчитывается величина:
Так как отношение двух выборочных дисперсий S 2 ф и S 2 ост распределено по закону Фишера-Снедекора, то полученное значение fнабл сравнивают со значением функции распределения
в критической точке fкр, соответствующей выбранному уровню значимости a.
Если fнабл>fкр, то фактор оказывает существенное воздействие и его следует учитывать, в противном случае он оказывает незначительное влияние, которым можно пренебречь.
Для расчета Rнабл и Rф могут быть использованы также формулы:
Rобщ=xij²- x ², (4)
Rф=q∑ x j²- x ², (5)
Находим общую среднюю по формуле (1):
Для расчета Rобщ по формуле (4) составляем таблицу 2 квадратов вариант:
| N | П 2 1 | П 2 2 |
| 1 | 144 | 289 |
| 2 | 324 | 361 |
| 3 | 529 | 625 |
| 4 | 100 | 49 |
| 5 | 225 | 289 |
| ∑ | 1322 | 1613 |
Общая средняя вычисляется по формуле (1):
Rобщ = 1322 + 1613 — 5 • 2 • 16.3 2 = 278.1
Находим Rф по формуле (5):
Rф = 5(15.6 2 + 17 2 ) — 2 • 16.3 2 = 4.9
Получаем Rост: Rост = Rобщ — Rф = 278.1 — 4.9 = 273.2
Определяем факторную и остаточную дисперсии:
Если средние значения случайной величины, вычисленные по отдельным выборкам одинаковы, то оценки факторной и остаточной дисперсий являются несмещенными оценками генеральной дисперсии и различаются несущественно.
Тогда сопоставление оценок этих дисперсий по критерию Фишера должно показать, что нулевую гипотезу о равенстве факторной и остаточной дисперсий отвергнуть нет оснований.
Оценка факторной дисперсии меньше оценки остаточной дисперсии, поэтому можно сразу утверждать справедливость нулевой гипотезы о равенстве математических ожиданий по слоям выборки.
Иначе говоря, в данном примере фактор Ф не оказывает существенного влияния на случайную величину.
Проверим нулевую гипотезу H: равенство средних значений х.
Находим fнабл
Для уровня значимости α=0.05, чисел степеней свободы 1 и 8 находим fкр из таблицы распределения Фишера-Снедекора.
fкр(0.05; 1; 8) = 5.32
В связи с тем, что fнабл Пример №1 . Произведено 13 испытаний, из них – 4 на первом уровне фактора, 4 – на втором, 3 – на третьем и 2 на четвертом. Методом дисперсионного анализа при уровне значимости 0,05 проверить нулевую гипотезу о равенстве групповых средних. Предполагается, что выборки извлечены из нормальных совокупностей с одинаковыми дисперсиями. Результаты испытаний приведены в таблице.
Решение:
Находим групповые средние:
| N | П1 | П2 | П3 | П4 |
| 1 | 1.38 | 1.41 | 1.32 | 1.31 |
| 2 | 1.38 | 1.42 | 1.33 | 1.33 |
| 3 | 1.42 | 1.44 | 1.34 | — |
| 4 | 1.42 | 1.45 | — | — |
| ∑ | 5.6 | 5.72 | 3.99 | 2.64 |
| x | 1.4 | 1.43 | 1.33 | 1.32 |
Обозначим р — количество уровней фактора (р=4). Число измерений на каждом уровне равно: 4,4,3,2
В последней строке помещены групповые средние для каждого уровня фактора.
Общая средняя вычисляется по формуле:
Для расчета Sобщ по формуле (4) составляем таблицу 2 квадратов вариант:
| N | П 2 1 | П 2 2 | П 2 3 | П 2 4 |
| 1 | 1.9 | 1.99 | 1.74 | 1.72 |
| 2 | 1.9 | 2.02 | 1.77 | 1.77 |
| 3 | 2.02 | 2.07 | 1.8 | — |
| 4 | 2.02 | 2.1 | — | — |
| ∑ | 7.84 | 8.18 | 5.31 | 3.49 |
Общую сумму квадратов отклонений находят по формуле:
Пример №2 . В школе 5 шестых классов. Психологу ставится задача, определить, одинаковый ли средний уровень ситуативной тревожности в классах. Для этого были приведены в таблице. Проверить уровень значимости α=0.05 предположение, что средняя ситуативная тревожность в классах не различается.
Пример №3 . Для изучения величины X произведено 4 испытания на каждом из пяти уровней фактора F. Результаты испытаний приведены в таблице. Выяснить, существенно ли влияние фактора F на величину X. Принять α = 0.05. Предполагается, что выборки извлечены из нормальных совокупностей с одинаковыми дисперсиями.
Пример №4 . Предположим, что в педагогическом эксперименте участвовали три группы студентов по 10 человек в каждой. В группах применили различные методы обучения: в первой – традиционный (F1), во второй – основанный на компьютерных технологиях (F2), в третьей – метод, широко использующий задания для самостоятельной работы (F3). Знания оценивались по десятибалльной системе.
Требуется обработать полученные данные об экзаменах и сделать заключение о том, значимо ли влияние метода преподавания, приняв за уровень значимости α=0.05.
Результаты экзаменов заданы таблицей, Fj – уровень фактора xij – оценка i-го учащегося обучающегося по методике Fj.
источник
Для чего применяется дисперсионный анализ? Цель дисперсионного анализа — исследование наличия или отсутствия существенного влияния какого-либо качественного или количественного фактора на изменения исследуемого результативного признака. Для этого фактор, предположительно имеющий или не имеющий существенного влияния, разделяют на классы градации (говоря иначе, группы) и выясняют, одинаково ли влияние фактора путём исследования значимости между средними в наборах данных, соответствующих градациям фактора. Примеры: исследуется зависимость прибыли предприятия от типа используемого сырья (тогда классы градации — типы сырья), зависимость себестоимости выпуска единицы продукции от величины подразделения предприятия (тогда классы градации — характеристики величины подразделения: большой, средний, малый).
Минимальное число классов градации (групп) — два. Классы градации могут быть качественными либо количественными.
Почему дисперсионный анализ называется дисперсионным? При дисперсионном анализе исследуется отношение двух дисперсий. Дисперсия, как мы знаем — характеристика рассеивания данных вокруг среднего значения. Первая — дисперсия, объяснённая влиянием фактора, которая характеризует рассеивание значений между градациями фактора (группами) вокруг средней всех данных. Вторая — необъяснённая дисперсия, которая характеризует рассеивание данных внутри градаций (групп) вокруг средних значений самих групп. Первую дисперсию можно назвать межгрупповой, а вторую — внутригрупповой. Отношение этих дисперсий называется фактическим отношением Фишера и сравнивается с критическим значением отношения Фишера. Если фактическое отношение Фишера больше критического, то средние классов градации отличаются друг от друга и исследуемый фактор существенно влияет на изменение данных. Если меньше, то средние классов градации не отличаются друг от друга и фактор не имеет существенного влияния.
Как формулируются, принимаются и отвергаются гипотезы при дисперсионном анализе? При дисперсионном анализе определяют удельный вес суммарного воздействия одного или нескольких факторов. Существенность влияния фактора определяется путём проверки гипотез:
- H 0 : μ 1 = μ 2 = . = μ a , где a — число классов градации — все классы градации имеют одно значение средних,
- H 1 : не все μ i равны — не все классы градации имеют одно значение средних.
Если влияние фактора не существенно, то несущественна и разница между классами градации этого фактора и в ходе дисперсионного анализа нулевая гипотеза H 0 не отвергается. Если влияние фактора существенно, то нулевая гипотеза H 0 отвергается: не все классы градации имеют одно и то же среднее значение, то есть среди возможных разниц между классами градации одна или несколько являются существенными.
Ещё некоторые понятия дисперсионного анализа. Статистическим комплексом в дисперсионном анализе называется таблица эмпирических данных. Если во всех классах градаций одинаковое число вариантов, то статистический комплекс называется однородным (гомогенным), если число вариантов разное — разнородным (гетерогенным).
В зависимости от числа оцениваемых факторов различают однофакторный, двухфакторый и многофакторный дисперсионный анализ.
Однофакторный дисперсионный анализ основан на том, что сумму квадратов отклонений статистического комплекса возможно разделить на компоненты:
SS — общая сумма квадратов отклонений,
SS a — объяснённая влиянием фактора a сумма квадратов отклонений,
SS e — необъяснённая сумма квадратов отклонений или сумма квадратов отклонений ошибки.
Если через n i обозначить число вариантов в каждом классе градации (группе) и a — общее число градаций фактора (групп), то 
общее число квадратов отклонений: 
объяснённая влиянием фактора a сумма квадратов отклонений: 
необъяснённая сумма квадратов отклонений или сумма квадратов отклонений ошибки: 


где 
Чтобы провести однофакторный дисперсионный анализ данных статистического комплекса, нужно найти фактическое отношение Фишера — отношение дисперсии, объяснённой влиянием фактора (межрупповой), и необъяснённой дисперсии (внутригрупповой):
и сравнить его с критическим значением Фишера 
Дисперсии рассчитываются следующим образом:


v a = a − 1 — число степеней свободы объяснённой дисперсии,
v e = n − a — число степеней свободы необъяснённой дисперсии,
v = n − 1 — общее число степеней свободы.
Критическое значение отношения Фишера с определёнными значениями уровня значимости и степеней свободы можно найти в статистических таблицах или рассчитать с помощью функции MS Excel F.ОБР (рисунок ниже, для его увеличения щёлкнуть по нему левой кнопкой мыши).
Функция требует ввести следующие данные:
Вероятность — уровень значимости α ,
Степени_свободы1 — число степеней свободы объяснённой дисперсии v a ,
Степени_свободы2 — число степеней свободы необъяснённой дисперсии v e .
Если фактическое значение отношения Фишера больше критического (
Если фактическое значение отношения Фишера меньше критического (
Пример 1. Требуется выяснить, влияет ли тип используемого сырья на прибыль предприятия. В шести классах градации (группах) фактора (1-й тип, 2-й тип и т.д.) собраны данные о прибыли от производства 1000 единиц продукции в миллионах рублей в течении 4 лет.
| Тип сырья | 2014 | 2015 | 2016 | 2017 |
| 1-й | 7,21 | 7,55 | 7,29 | 7,6 |
| 2-й | 7,89 | 8,27 | 7,39 | 8,18 |
| 3-й | 7,25 | 7,01 | 7,37 | 7,53 |
| 4-й | 7,75 | 7,41 | 7,27 | 7,42 |
| 5-й | 7,7 | 8,28 | 8,55 | 8,6 |
| 6-й | 7,56 | 8,05 | 8,07 | 7,84 |
Среднее  | Дисперсия  |
| 7,413 | 0,0367 |
| 7,933 | 0,1571 |
| 7,290 | 0,0480 |
| 7,463 | 0,0414 |
| 8,283 | 0,1706 |
| 7,880 | 0,0563 |
Число классов градации фактора (групп) a = 6 и в каждом классе (группе) n i = 4 наблюдения. Общее число наблюдений n = 24 .
Вычислим суммы квадратов отклонений:

Вычислим фактическое отношение Фишера:

Критическое значение отношения Фишера:
Так как фактическое отношение Фишера больше критического:

с уровнем значимости α = 0,05 делаем вывод, что прибыль предприятия в зависимости от вида сырья, использованного в производстве, существенно отличается.
Или, что то же самое, отвергаем основную гипотезу о равенстве средних во всех классах градации фактора (группах).
В только что рассмотренном примере в каждом классе градации фактора было одинаковое число вариантов. Но, как говорилось во вступительной части, число вариантов может быть и разным. И это ни в коей мере не усложняет процедуру дисперсионного анализа. Таков следующий пример.
Пример 2. Требуется выяснить, существует ли зависимость себестоимости выпуска единицы продукции от величины подразделения предприятия. Фактор (величина подразделения) делится на три класса градации (группы): малые, средние, большие. Обобщены соответствующие этим группам данные о себестоимости выпуска единицы одного и того же вида продукции за некоторый период.
| малый | средний | большой | |
| 48 | 47 | 46 | |
| 50 | 61 | 57 | |
| 63 | 63 | 57 | |
| 72 | 47 | 55 | |
| 43 | 32 | ||
| 59 | 59 | ||
| 58 | |||
Среднее  | 58,6 | 54,0 | 51,0 |
Дисперсия  | 128,25 | 65,00 | 107,60 |
Число классов градации фактора (групп) a = 3 , число наблюдений в классах (группах) n 1 = 4 , n 2 = 7 , n 3 = 6 . Общее число наблюдений n = 17 .
Вычислим суммы квадратов отклонений:


Вычислим фактическое отношение Фишера:

Критическое значение отношения Фишера:

Так как фактическое значение отношения Фишера меньше критического: 
Или, что то же самое, с вероятностью 95% принимаем основную гипотезу о том, что средняя себестоимость выпуска единицы одной и той же продукции в малых, средних и крупных подразделениях предприятия существенно не различается.
Однофакторный дисперсионный анализ можно провести с помощью процедуры MS Excel Однофакторный дисперсионный анализ. Используем его для анализа данных о связи типа используемого сырья и прибыли предприятия из примера 1.
В меню MS Excel выполняем команду Сервис/Анализ данных и выбираем средство анализа Однофакторный дисперсионный анализ.
В окошке Входной интервал указываем область данных (в нашем случае это $A$2:$E$7). Указываем, как сгруппирован фактор — по столбцам или по строкам (в нашем случае по строкам). Если первый столбец содержит названия классов фактора, помечаем галочкой окно Метки в первом столбце. В окне Альфа указываем уровень значимости α = 0,05 .
В результате действия процедуры выводятся две таблицы. Первая таблица — Итоги. В ней содержатся данные обо всех классах градации фактора: число наблюдений, суммарное значение, среднее значение и дисперсия.
Во второй таблице — Дисперсионный анализ — содержатся данные о величинах для фактора между группами и внутри групп и итоговых. Это сумма квадратов отклонений (SS), число степеней свободы (df), дисперсия (MS). В последних трёх столбцах — фактическое значение отношения Фишера(F), p-уровень (P-value) и критическое значение отношения Фишера (F crit).
| Дисперсионный анализ | ||
| Источник вариации | SS | df |
| Между группами | 2,9293 | 5 |
| Внутри групп | 1,5303 | 18 |
| Итого | 4,4596 | 23 |
Так как фактическое значение отношения Фишера (6,89) больше критического (2,77), с вероятностью 95% отклоняем нулевую гипотезу о равенстве средних производительности при использовании всех типов сырья, то есть делаем вывод о том, что тип используемого сырья влияет на прибыль предприятия.
Двухфакторный дисперсионный анализ применяется для того, чтобы проверить возможную зависимость результативного признака от двух факторов — A и B. Тогда a — число градаций фактора A и b — число градаций фактора B. В статистическом комплексе сумма квадратов остатков разделяется на три компоненты:







Дисперсии вычисляются следующим образом:



v a = a − 1 — число степеней свободы дисперсии, объяснённой влиянием фактора A ,
v b = b − 1 — число степеней свободы дисперсии, объяснённой влиянием фактора B ,
v e = (a − 1)(b − 1) — число степеней свободы необъяснённой дисперсии или дисперсии ошибки,
v = ab − 1 — общее число степеней свободы.
Если факторы не зависят друг от друга, то для определения существенности факторов выдвигаются две нулевые гипотезы и соответствующие альтернативные гипотезы:
Чтобы определить влияние фактора A , нужно фактическое отношение Фишера 

Чтобы определить влияние фактора B , нужно фактическое отношение Фишера 

Если фактическое отношение Фишера больше критического отношения Фишера, то следует отклонить нулевую гипотезу с уровнем значимости α . Это означает, что фактор существенно влияет на данные: данные зависят от фактора с вероятностью P = 1 − α .
Если фактическое отношение Фишера меньше критического отношения Фишера, то следует принять нулевую гипотезу с уровнем значимости α . Это означает, что фактор не оказывает существенного влияния на данные с вероятностью P = 1 − α .
Пример 3. Дана информация о среднем потреблении топлива на 100 километров в литрах в зависимости от объёма двигателя и вида топлива.
| Бензин со свинцом | |
| 1001-1500 см³ | 9,3 |
| 1501-2000 см³ | 9,4 |
| Более 2000 см³ | 12,6 |
Среднее  | 10,42 |
| Бензин без свинца | Дизельное топливо | Среднее  |
| 8,9 | 6,5 | 8,23 |
| 9,1 | 7,1 | 8,53 |
| 9,8 | 8,0 | 10,13 |
| 9,27 | 7,2 |
Требуется проверить, зависит ли потребление топлива от объёма двигателя и вида топлива.
Решение. Для фактора A число классов градации a = 3 , для фактора B число классов градации b = 3 .
Вычисляем суммы квадратов отклонений:







Фактическое отношение Фишера для фактора A 


Фактическое отношение Фишера для фактора B 

Двухфакторный дисперсионный анализ без повторений можно провести с помощью процедуры MS Excel Двухфакторный дисперсионный анализ без повторений. Используем его для анализа данных о связи типа вида топлива и его потребления из примера 3.
В меню MS Excel выполняем команду Сервис/Анализ данных и выбираем средство анализа Двухфакторный дисперсионный анализ без повторений.
Заполняем данные также, как и в случае с однофакторным дисперсионным анализом.
В результате действия процедуры выводятся две таблицы. Первая таблица — Итоги. В ней содержатся данные обо всех классах градации фактора: число наблюдений, суммарное значение, среднее значение и дисперсия.
Во второй таблице — Дисперсионный анализ — содержатся данные об источниках вариации: рассеивании между строками, рассеивании между столбцами, рассеивании ошибки, общем рассеивании, сумма квадратов отклонений (SS), число степеней свободы (df), дисперсия (MS). В последних трёх столбцах — фактическое значение отношения Фишера(F), p-уровень (P-value) и критическое значение отношения Фишера (F crit).
| Дисперсионный анализ | ||
| Источник вариации | SS | df |
| Строки | 6,26 | 2 |
| Столбцы | 16,08667 | 2 |
| Погрешность | 2,373333 | 4 |
| Итого | 24,72 | 8 |
Фактор A (объём двигателя) сгурппирован в строках. Так как фактическое отношение Фишера 5,28 меньше критического 6,94, с вероятностью 95% принимаем, что потребление топлива не зависит от объёма двигателя.
Фактор B (вид топлива) сгруппирован в столбцах. Фактическое отношение Фишера 13,56 больше критического 6,94, поэтому с вероятностью 95% принимаем, что потребление топлива зависит от его вида.
Двухфакторный дисперсионный анализ с повторениями применяется для того, чтобы проверить не только возможную зависимость результативного признака от двух факторов — A и B, но и возможное взаимодействие факторов A и B. Тогда a — число градаций фактора A и b — число градаций фактора B, r — число повторений. В статистическом комплексе сумма квадратов остатков разделяется на четыре компоненты:









n = abr — общее число наблюдений.
Дисперсии вычисляются следующим образом:




v a = a − 1 — число степеней свободы дисперсии, объяснённой влиянием фактора A ,
v b = b − 1 — число степеней свободы дисперсии, объяснённой влиянием фактора B ,
v ab = (a − 1)(b − 1) — число степеней свободы дисперсии, объяснённой взаимодействием факторов A и B ,
v e = ab(r − 1) — число степеней свободы необъяснённой дисперсии или дисперсии ошибки,
v = abr − 1 — общее число степеней свободы.
Если факторы не зависят друг от друга, то для определения существенности факторов выдвигаются три нулевые гипотезы и соответствующие альтернативные гипотезы:
для взаимодействия факторов A и B :
Чтобы определить влияние фактора A , нужно фактическое отношение Фишера 

Чтобы определить влияние фактора B , нужно фактическое отношение Фишера 

Чтобы определить влияние взаимодействия факторов A и B , нужно фактическое отношение Фишера 

Если фактическое отношение Фишера больше критического отношения Фишера, то следует отклонить нулевую гипотезу с уровнем значимости α . Это означает, что фактор существенно влияет на данные: данные зависят от фактора с вероятностью P = 1 − α .
Если фактическое отношение Фишера меньше критического отношения Фишера, то следует принять нулевую гипотезу с уровнем значимости α . Это означает, что фактор не оказывает существенного влияния на данные с вероятностью P = 1 − α .
Пример 4. Торговое предприятие имеет три магазина — A , B и C . Проводятся две рекламные кампании. Требуется выяснить, зависят ли средние дневные доходы магазинов от двух рекламных кампаний. Для процедуры проверки случайно выбраны по 3 дня каждой рекламной кампании (то есть число повторений r = 3 ). Результаты обобщены в таблице:
| Рекламная кампания | Магазин A |
| Рекламная кампания 1 | 12,05 |
| 23,94 | |
| 14,63 | |
| Рекламная кампания 2 | 25,78 |
| 17,52 | |
| 18,45 | |
Среднее  | 18,73 |
| Магазин B | Магазин C | Среднее  |
| 15,17 | 9,48 | 14,53 |
| 18,52 | 6,92 | |
| 19,57 | 10,47 | |
| 21,40 | 7,63 | 15,86 |
| 13,59 | 11,90 | |
| 20,57 | 5,92 | |
| 18,14 | 8,72 |  |
Факторы, подлежащие проверке: магазин ( A , B и C ) и рекламная кампания (1 и 2). Пусть эти факторы не зависят друг от друга.
Вычислим суммы квадратов отклонений:
v = abr − 1 = 2 ⋅ 3 ⋅ 3 − 1 = 17 .




Фактические отношения Фишера:
для фактора A :
для фактора B :
для взаимодействия факторов A и B : 
Критические значения отношения Фишера:
для фактора A : 
для фактора B :
для взаимодействия факторов A и B : 
о влиянии фактора A : фактическое отношение Фишера меньше критического значения, следовательно, рекламная кампания существенно не влияет на дневные доходы магазина с вероятностью 95%,
о влиянии фактора B : фактическое отношение Фишера больше критического, следовательно, доходы существенно различаются между магазинами,
о взаимодействии факторов A и B : фактическое отношение Фишера меньше критического, следовательно, взаимодействие рекламной кампании и конкретного магазина не существенно.
Двухфакторный дисперсионный анализ с повторениями можно провести с помощью процедуры MS Excel Двухфакторный дисперсионный анализ с повторениями. Используем его для анализа данных о связи доходов магазина с выбором конкретного магазина и рекламной кампанией из примера 4.
В меню MS Excel выполняем команду Сервис/Анализ данных и выбираем средство анализа Двухфакторный дисперсионный анализ с повторениями.
Заполняем данные также, как и в случае с двухфакторным дисперсионным анализом без повторений, с тем дополнением, что в окне число строк для выборки нужно ввести число повторений.
В результате действия процедуры выводятся две таблицы. Первая таблица состоит из трёх частей: две первые соответствуют каждой из двух рекламных кампаний, третья содержит данные об обеих рекламных кампаниях. В столбцах таблицы содержится информация обо всех классах градации второго фактора — магазина: число наблюдений, суммарное значение, среднее значение и дисперсия.
Во второй таблице — данные о сумме квадратов отклонений (SS), числе степеней свободы (df), дисперсии (MS), фактическом значение отношения Фишера(F), p-уровне (P-value) и критическом значении отношения Фишера (F crit) для различных источниках вариации: двух факторах, которые даны в строках (выборка) и столбцах, взаимодействии факторов, ошибки (внутри) и суммарных показателях (итого).
| Дисперсионный анализ | ||
| Источник вариации | SS | df |
| Выборка | 8,013339 | 1 |
| Столбцы | 378,3808 | 2 |
| Взаимодействие | 13,8504 | 2 |
| Внутри | 192,2233 | 12 |
| Итого | 592,4681 | 17 |
| MS | F | P-value | F crit |
| 8,013339 | 0,500252 | 0,492897 | 4,747221 |
| 189,1904 | 11,81066 | 0,001462 | 3,88529 |
| 6,925272 | 0,432327 | 0,658717 | 3,88529 |
| 16,01861 |
Для фактора A фактическое отношение Фишера меньше критического значения, следовательно, рекламная кампания существенно не влияет на дневные доходы магазина с вероятностью 95%.
Для фактора B фактическое отношение Фишера больше критического, следовательно, с вероятностью 95% доходы существенно различаются между магазинами.
Для взаимодействия факторов A и B фактическое отношение Фишера меньше критического, следовательно, с вероятностью 95% взаимодействие рекламной кампании и конкретного магазина не существенно.
источник