Анализ сигналов как по английски

Другие результаты
Если задано, что сигнал периодический, то анализатор понимает заданный в редакторе сигнал как один период.	If is given, that a signal periodic, the analyzer understands specific in the editor a signal as one period.
А пока Касл будет скачивать, я отслежу сигнал с помощью wi-fi анализатора на моем телефоне.	And while Castle’s downloading, I’ll track the signal using the wi-fi analyzer on my phone.
Водородный анализатор должен быть оснащен устройством для регистрации выходного электрического сигнала с частотой по меньшей мере один раз в минуту.	The hydrogen analyser shall be fitted with a device to record electrical signal output, at a frequency of at least once per minute.
Анализаторы сигнала — аппаратура, способная измерять и отображать основные характеристики одночастотной составляющей из многочастотного сигнала.	Signal generators, frequency synthesizer based Conventional Section: p. 198, 3.A..d.
Expert Advisors или EAs проводит быстрый технический анализ данных цен и автоматически исполняет биржевые решения на основании любого полученного сигнала.	Expert Advisors or EAs perform quick technical analysis of price data and will automatically execute trading decisions based on any signal received.
Ученые анализировали первые два сигнала, а к ним поступали все новые. В январе они представили материалы своего исследования в журнале Physical Review Letters. Этот номер выходит в интернет-версии сегодня.	The scientists analyzed these first two signals as even more swept in, and they submitted their paper to Physical Review Letters in January; it appeared online today.
Посмотри на этот список . анализы крови, финансовые отчеты, домашнее обучение, пожарная сигнализация.	Look at this list. blood work, financial statements, a home study, I mean, fire alarms.
Я сделал технический анализ этих сигналов и связал их с соответствующими цифрами.	I had a tech analyze those beeps And connect them to the corresponding digits.
Производят анализ цифровых записей сейсмических сигналов в скользящем временном окне.	The digital recordings of the seismic signals are analyzed in a sliding time window.
Значение этих сигналов используются для проверки полученных результатов с методом регрессионного анализа после каждого испытания.	These signals are used in the regression checks performed after each test of the reference flowmeter shall be subtracted from this value.
Концентрации СО, CO2 и NMHC могут определяться интегрированием непрерывных сигналов измерения или методом анализа концентраций этих веществ, накопившихся в мешке для отбора проб в течение цикла.	CO, CO2, and NMHC may be determined by integration of continuous measurement signals or by analyzing the concentrations in the sample bag, collected over the cycle.
Хотя их анализ может показаться довольно ограничивающим и включает в себя некоторые предположения, это не имеет значения: интерпретация биологических сигналов должна быть безупречной.	While their analysis might seem quite restrictive and involves a number of assumptions, it does not really matter: interpretation of biosignatures needs to be flawless.
Было понятно, что задача Ту-95РЦ состоит в анализе радио- и радиолокационных сигналов с авианосца и с его самолетов в небе.	It was obvious the D’s mission was to analyze the radar and communications signals from the Forrestal and its airborne aircraft.
Итак, анализируя сигналы вашего головного мозга, мы можем отследить, куда именно вы смотрите или на что вы обращаете внимание.	So by analyzing your brain signals, we can track where exactly you are watching or you are paying attention to.
Более 50 встроенных индикаторов технического анализа, которые помогут Вам следовать рынку и обнаруживать торговые возможности и сигналы для оптимального открытия и закрытия сделок	Over 50 built-in technical indicators to help you follow the market and discover trading patterns and signals for entry and exit points
При анализе графиков различают следующие сигналы Relative Strenght Index:	Ways to use Relative Strength Index for chart analysis:

источник

Английское слово wavelet (от французского «ondelette») дословно переводится как «короткая (маленькая) волна». В различных переводах зарубежных статей на русский язык встречаются еще термины: «всплеск», «всплесковая функция», «маловолновая функция», «волночка» и др.

Вейвлет-преобразование (ВП) широко используется для анализа сигналов. Помимо этого, оно находит большое применение в области сжатия данных. ВП одномерного сигнала – это его представление ввиде обобщенного ряда или интеграла Фурье по системе базисных функций.

, (1)

сконструированных из материнского (исходного) вейвлета , обладающего определенными свойствами за счет операций сдвига во времени ( b ) и изменения временного масштаба (a).

Множитель обеспечивает независимость нормы функций (1) от масштабирующего числа (a). Для заданных значений параметров a и b функция и есть вейвлет, порождаемый материнским вейвлетом .

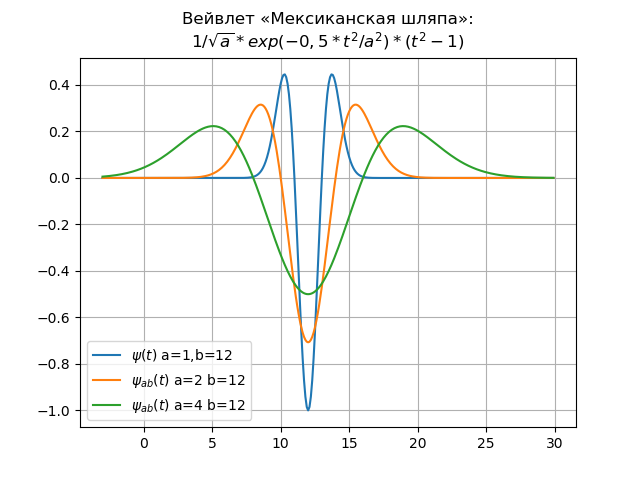
В качестве примера приведём вейвлет «мексиканская шляпа» во временной и частотной областях:

1.Между концепцией гармоник Фурье и масштабом вейвлета действительно существует взаимосвязь. Главное в этой взаимосвязи — обратная пропорциональность собственной частоты и масштаба. Кроме этого, уменьшая масштаб, мы увеличиваем полосу пропускания спектра вейвлета.

2. За счет изменения масштаба (увеличение a приводит к сужению фурье-спектра функции ), вейвлеты способны выявлять различие в характеристиках на разных шкалах (частотах), а за счет сдвига- проанализировать свойства сигнала в разных точках на всем исследуемом интервале. Поэтому, при анализе нестационарных сигналов, за счет свойства локальности вейвлетов, получают существенное преимущество перед преобразованием Фурье, которое дает только глобальные сведения о частотах (масштабах) анализируемого сигнала, так как используемая при этом система функций (комплексная экспонента или синусы и косинусы) определена на бесконечном интервале.

3. Приведенные листинги, написанные на свободно распространяемом языке высокого уровня Python позволяют подбирать функции для вейвлетов, отвечающие заданным требованиям. Однако, при этом дополнительно необходимо учесть все главные признаки вейвлетов.

Ограниченность. Квадрат нормы функции должен быть конечным:
. (2)

Локализация. ВП в отличие от преобразования Фурье использует локализованную исходную функцию и во времени, и по частоте. Для этого достаточно, чтобы выполнялись условия:

и
при 0$» data-tex=»inline»> , (3)

Например, дельта-функция и гармоническая функция не удовлетворяют необходимому условию одновременной локализации во временной и частотной областях.

Нулевое среднее. График исходной функции должен осциллировать (быть знакопеременным) вокруг нуля на оси времени и иметь нулевую площадь:

. (4)

Из этого условия становится понятным выбор названия «вейвлет» – маленькая волна.

Равенство нулю площади функции , т.е. нулевого момента, приводит к тому, что фурье-преобразование этой функции равно нулю при и имеет вид полосового фильтра. При различных значениях (a) это будет набор полосовых фильтров.

Часто для приложений бывает необходимо, чтобы не только нулевой, но и все первые n моментов были равны нулю:

. (5)

Вейвлеты n -го порядка позволяют анализировать более тонкую (высокочастотную) структуру сигнала, подавляя медленно изменяющиеся его составляющие.

Автомодельность. Характерным признаком ВП является его самоподобие. Все вейвлеты конкретного семейства имеют то же число осцилляций, что и материнский вейвлет , поскольку получены из него посредством масштабных преобразований ( a ) и сдвига ( b ).

Непрерывное (интегральное) вейвлет-преобразование (НВП или СWT – continuous wavelet transform). Сконструируем базис с помощью непрерывных масштабных преобразований (a) и переносов (b) материнского вейвлета с произвольными значениями базисных параметров a и b в формуле (1).

Тогда, по определению прямое (анализ) и обратное (синтез) HВП (т.е. ПНВП и ОНВП) сигнала S(t) запишутся так:
, (6)

, (7)

где – нормирующий коэффициент,

где: (•,•) – скалярное произведение соответствующих сомножителей,
– фурье-преобразование вейвлета . Для ортонормированных вейвлетов .

Из (6) следует, что вейвлет-спектр (wavelet spectrum, или time-scale-spectrum – масштабно-временной спектр) в отличие от фурье-спектра (single spectrum) является функцией двух аргументов: первый аргумент а (временной масштаб) аналогичен периоду осцилляций, т.е. обратен частоте, а второй b–аналогичен смещению сигнала по оси времени.

Следует отметить, что характеризует временную зависимость (при , тогда как зависимости можно поставить в соответствие частотную зависимость (при ).

Если исследуемый сигнал S(t) представляет собой одиночный импульс длительностью , сосредоточенный в окрестности , то его вейвлет-спектр будет иметь наибольшее значение в окрестности точки с координатами .

Способы представления (визуализации) могут быть различными. Спектр является поверхностью в трехмерном пространстве. Однако, часто вместо изображения поверхности представляют её проекцию на плоскость ab с изоуровнями (или фигурами различных цветов), позволяющими проследить изменение интенсивности амплитуд ВП на разных масштабах (а) и во времени (b ).

Кроме того, изображают картины линий локальных экстремумов этих поверхностей, так называемый скелетон (sceleton), который выявляет структуру анализируемого сигнала.

Непрерывное вейвлет преобразование при определении вейвлет спектра на основе материнского вейвлета -«мексиканская шляпа».

Применяются и другие материнские вейвлеты используемые для НВП:

Непрерывное ВП нашло широкое применение в обработке сигналов. В частности, вейвлет-анализ (ВА) дает уникальные возможности распознавать локальные и «тонкие» особенности сигналов (функций), что важно во многих областях радиотехники, связи, радиоэлектроники, геофизики и других отраслях науки и техники. Рассмотрим эту возможность на некоторых простейших примерах.

Сигнал имеет вид:

где:

Вейвлетобразующая функция: ,

Вейвлеты: ,

Вейвлет-спектр: N:=256, a:=1..30, b:=0..50, .

График двухпараметрического спектра выведен в виде поверхности в трехмерном пространстве.

Следует отметить, что сечение W(a,b) для временного масштаба характеризует исходное колебание s(t). При этом амплитуда его максимальна при . Зависимости можно поставить в соответствие текущий спектр колебания при .

Сумма двух гармонических колебаний.

Сигнал имеет вид :

где: .

, N:=256,
, a:=1. 30, b:=0. 50, .

График двухпараметрического спектра W(a,b) выведен виде поверхности в трехмерном пространстве.

Плоскость параметров a,b на которой результаты ВП выделены цветными областями.

На графике приведены «сечения» вейвлет-спектра для двух значений параметра а. При относительно небольшом параметре временного масштаба a, при , сечение спектра несет информацию только о высокочастотной составляющей сигнала, отфильтровывая (подавляя) его низкочастотный компонент.

С ростом a происходит растяжение базисной функции , следовательно, сужение ее спектра, и сужению полосы пропускания частотного «окна». В результате при сечение спектра представляет собой лишь низкочастотный компонент сигнала.

При дальнейшем увеличении a полоса окна еще уменьшается и уровень этого низкочастотного компонента убывает до постоянной составляющей (при a >25), равной нулю для анализируемого сигнала.

На графике приведены сечения вейвлет-спектра W(a,b), характеризующие
текущий спектр сигнала при и . Спектр рассматриваемого сигнала в отличие от гармонического содержит высокочастотный компонент в области малых значений временного масштаба a(a:1..3), который соответствует второй составляющей сигнала .

Вейвлет-спектры приведены в графиках, вейвлет-спектр хорошо передает тонкие особенности сигнала – его скачки на отсчетах b =20 и b =80 (при a:1..10).

Эта публикация носит учебный характер, в ней приведены основные сведения о вейвлет- анализе в целом, а на простых примерах на свободно распространяемом высокоуровневом языке программирования Python показаны особенности непрерывного вейвлет-анализа с обширной графической 3D и 2D визуализацией.

источник

Спектроанализатор – прибор для измерения и отображения спектра сигнала – распределения энергии сигнала по частотам. В этой статье рассматриваются основные виды анализаторов спектра и иллюстрируется их применение для редактирования и реставрации звука. Особое внимание уделяется современным анализаторам, основанным на FFT – быстром преобразовании Фурье.

Традиционно в цифровой звукозаписи аудиодорожка представляется в виде осциллограммы, отображающей форму звуковой волны (waveform), то есть зависимость амплитуды звука от времени. Такое представление достаточно наглядно для опытного звукорежиссёра: осциллограмма позволяет увидеть основные события в звуке, такие как изменения громкости, паузы между частями произведения и зачастую даже отдельные ноты в сольной записи инструмента. Но одновременное звучание нескольких инструментов на осциллограмме «смешивается» и визуальный анализ сигнала становится затруднительным. Тем не менее, наше ухо без труда различает отдельные инструменты в небольшом ансамбле. Как же это происходит?

Когда сложное звуковое колебание попадает на барабанную перепонку уха, оно с помощью серии слуховых косточек передаётся на орган, называемый улиткой. Улитка представляет собой закрученную в спираль эластичную трубочку. Толщина и жёсткость улитки плавно меняются от края к центру спирали. Когда сложное колебание поступает на край улитки, это вызывает ответные колебания разных частей улитки. При этом резонансная частота у каждой части улитки своя. Таким образом улитка раскладывает сложное звуковое колебание на отдельные частотные составляющие. К каждой части улитки подходят отдельные группы слуховых нервов, передающие информацию о колебаниях улитки в головной мозг (более подробно о слуховом восприятии можно прочитать в статье «Основы психоакустики» И. Алдошиной в журнале «Звукорежиссер» №6, 1999). В результате в мозг поступает информация о звуке, уже разложенная по частотам, и человек легко отличает высокие звуки от низких. Кроме того, как мы вскоре увидим, разложение звука на частоты помогает различить отдельные инструменты в полифонической записи, что значительно расширяет возможности редактирования.

Первые звуковые анализаторы спектра разделяли сигнал на частотные полосы с помощью набора аналоговых фильтров. Дисплей такого анализатора (рис. 1) показывает уровень сигнала во множестве частотных полос, соответствующих фильтрам.

На рис. 2 приведён пример частотных характеристик полосовых фильтров в анализаторе, удовлетворяющем стандарту ГОСТ 17168-82. Такой анализатор называется третьоктавным, так как в каждой октаве частотного диапазона имеется три полосы. Видно, что частотные характеристики полосовых фильтров перекрываются; их крутизна зависит от порядка используемых фильтров.

Важным свойством спектроанализатора является баллистика – инерционность измерителей уровня в частотных полосах. Она может регулироваться заданием скорости нарастания (атаки) и спада уровня. Типичное время атаки и спада в таком анализаторе – порядка 200 и 1500 мс.

Полосовые спектроанализаторы часто применяются для настройки АЧХ (амплитудно-частотной характеристики) акустических систем на концертных площадках. Если на вход такому анализатору подать розовый шум (имеющий одинаковую мощность в каждой октаве), то дисплей покажет горизонтальную линию, с возможной поправкой на вариацию шума во времени. Если розовый шум, проходя через звукоусилительную систему зала, исказился, то изменения его спектра будут видны на анализаторе. При этом анализатор, как и наше ухо, будет малочувствителен к узким провалам АЧХ (менее 1/3 октавы).

Преобразование Фурье – это математический аппарат для разложения сигналов на синусоидальные колебания. Например, если сигнал x(t) непрерывный и бесконечный по времени, то его можно представить в виде интеграла Фурье:

Интеграл Фурье собирает сигнал x(t) из бесконечного множества синусоидальных составляющих всевозможных частот ω, имеющих амплитуды X_ω и фазы φ_ω.

На практике нас больше интересует анализ конечных по времени звуков. Поскольку музыка не является статичным сигналом, её спектр меняется во времени. Поэтому при спектральном анализе нас обычно интересуют отдельные короткие фрагменты сигнала. Для анализа таких фрагментов цифрового аудиосигнала существует дискретное преобразование Фурье:

Здесь N отсчётов дискретного сигнала x(n) на интервале времени от 0 до N–1 синтезируются как сумма конечного числа синусоидальных колебаний с амплитудами X_k и фазами φ_k. Частоты этих синусоид равны kF/N, где F – частота дискретизации сигнала, а N – число отсчётов исходного сигнала x(n) на анализируемом интервале. Набор коэффициентов X_k называется амплитудным спектром сигнала. Как видно из формулы, частоты синусоид, на которые раскладывается сигнал, равномерно распределены от 0 (постоянная составляющая) до F/2 – максимально возможной частоты в цифровом сигнале. Такое линейное расположение частот отличается от распределения полос третьоктавного анализатора.

FFT (fast Fourier transform) – алгоритм быстрого вычисления дискретного преобразования Фурье. Благодаря ему стало возможным анализировать спектр звуковых сигналов в реальном времени.

Рассмотрим работу типичного FFT-анализатора. На вход ему поступает цифровой аудиосигнал. Анализатор выбирает из сигнала последовательные интервалы («окна»), на которых будет вычисляться спектр, и считает FFT в каждом окне для получения амплитудного спектра X_k. Вычисленный спектр отображается в виде графика зависимости амплитуды от частоты (рис. 3). Аналогично полосовым анализаторам, обычно используется логарифмический масштаб по осям частот и амплитуд. Но из-за линейного расположения полос FFT по частоте спектр может выглядеть недостаточно детальным на нижних частотах или излишне осциллирующим на верхних частотах.

Если рассматривать FFT как набор фильтров, то, в отличие от полосовых фильтров третьоктавного анализатора, фильтры FFT будут иметь одинаковую ширину в герцах, а не в октавах. Поэтому розовый шум на FFT-анализаторе будет уже не горизонтальной линией, а наклонной, со спадом 3 дБ/окт. Горизонтальной линией на FFT-анализаторе будет белый шум – он содержит равную энергию в равных линейных частотных интервалах.

Параметр N – число анализируемых отсчётов сигнала – имеет решающее значение для вида спектра. Чем больше N, тем плотнее сетка частот, по которым FFT раскладывает сигнал, и тем больше деталей по частоте видно на спектре. Для достижения более высокого частотного разрешения приходится анализировать более длинные участки сигнала. Если сигнал в пределах окна FFT меняет свои свойства, то спектр будет отображать некоторую усреднённую информацию о сигнале со всего интервала окна.

Когда нужно проанализировать быстрые изменения в сигнале, длину окна N выбирают маленькой. В этом случае разрешение анализа по времени увеличивается, а по частоте – уменьшается. Таким образом, разрешение анализа по частоте обратно пропорционально разрешению по времени. Этот факт называется соотношением неопределённостей.

Один из простейших звуковых сигналов – синусоидальный тон. Как будет выглядеть его спектр на FFT-анализаторе? Оказывается, это зависит от частоты тона. Мы знаем, что FFT раскладывает сигнал не по тем частотам, которые на самом деле присутствуют в сигнале, а по фиксированной равномерной сетке частот. Например, если частота дискретизации равна 48 кГц и размер окна FFT выбран 4096 отсчётов, то FFT раскладывает сигнал по 2049 частотам: 0 Гц, 11.72 Гц, 23.44 Гц, . 24000 Гц.

Если частота тона совпадает с одной из частот сетки FFT, то спектр будет выглядеть «идеально»: единственный острый пик укажет на частоту и амплитуду тона (рис. 4, белый график).

Если же частота тона не совпадает ни с одной из частот сетки FFT, то FFT «соберёт» тон из имеющихся в сетке частот, скомбинированных с различными весами. График спектра при этом размывается по частоте (рис. 4, зелёный график). Такое размытие обычно нежелательно, так как оно может закрыть собой более слабые звуки на соседних частотах. Можно также заметить, что амплитуда максимума зелёного графика ниже реальной амплитуды анализируемого тона. Это связано с тем, что мощность анализируемого тона равна сумме мощностей коэффициентов спектра, из которых этот тон составлен.

(наведите мышь для выбора изображения)

Чтобы уменьшить эффект размытия спектра, сигнал перед вычислением FFT умножается на весовые окна – гладкие функции, похожие на гауссиан, спадающие к краям интервала. Они уменьшают размытие спектра за счёт некоторого ухудшения частотного разрешения. Если рассматривать FFT как набор полосовых фильтров, то весовые окна регулируют взаимное проникновение частотных полос.

Простейшее окно – прямоугольное: это константа 1, не меняющая сигнала. Оно эквивалентно отсутствию весового окна. Одно из популярных окон – окно Хэмминга. Оно уменьшает уровень размытия спектра примерно на 40 дБ относительно главного пика.

Весовые окна различаются по двум основным параметрам: степени расширения главного пика и степени подавления размытия спектра («боковых лепестков»). Чем сильнее мы хотим подавить боковые лепестки, тем шире будет основной пик. Прямоугольное окно меньше всего размывает верхушку пика, но имеет самые высокие боковые лепестки. Окно Кайзера обладает параметром, который позволяет выбирать нужную степень подавления боковых лепестков.

Другой популярный выбор – окно Хана. Оно подавляет максимальный боковой лепесток слабее, чем окно Хэмминга, но зато остальные боковые лепестки быстрее спадают при удалении от главного пика. Окно Блэкмана обладает более сильным подавлением боковых лепестков, чем окно Хана.

Для большинства задач не очень важно, какой именно вид весового окна использовать. Главное, чтобы оно было. Популярный выбор – Хан или Блэкман. Использование весового окна уменьшает зависимость формы спектра от конкретной частоты сигнала и от её совпадения с сеткой частот FFT.

Рисунок 4 сделан для синусоид, однако, исходя из него, нетрудно представить, как будет выглядеть спектр реальных звуковых сигналов. Каждый пик в спектре будет иметь некоторую размытую форму, в зависимости от своей частоты и выбранного весового окна.

Чтобы компенсировать расширение пиков при применении весовых окон, можно использовать более длинные окна FFT: например, не 4096, а 8192 отсчета. Это улучшит разрешение анализа по частоте, но ухудшит по времени.

Часто возникает необходимость проследить, как спектр сигнала меняется во времени. FFT-анализаторы помогают сделать это в реальном времени при воспроизведении сигнала. Однако в ряде случаев оказывается удобна визуализация изменения спектра во всём звуковом отрывке сразу. Такое представление сигнала называется спектрограммой. Для её построения применяется оконное преобразование Фурье: спектр вычисляется от последовательных окон сигнала (рис. 5), и каждый из этих спектров образует столбец в спектрограмме.

По горизонтальной оси спектрограммы откладывается время, по вертикальной – частота, а амплитуда отображается яркостью или цветом. На спектрограмме гитарной ноты на рис. 6 видно развитие звучания: оно начинается с резкой атаки и продолжается в виде гармоник, кратных по частоте основному тону 440 Гц. Видно, что верхние гармоники имеют меньшую амплитуду и затухают быстрее, чем нижние. Также на спектрограмме прослеживается шум записи – равномерный фон тёмно-синего цвета. Справа показана шкала соответствия цветов и уровней сигнала (в децибелах ниже нуля).

(наведите мышь для выбора изображения)

Если менять размер окна FFT, становится хорошо видно, как меняется частотное и временное разрешение спектрограммы. При увеличении окна гармоники становятся тоньше, и их частота может быть определена более точно. Однако размывается во времени момент атаки (в левой части спектрограммы). При уменьшении размера окна наблюдается обратный эффект.

Особенно полезна спектрограмма при анализе быстро меняющихся сигналов. На рис. 7 показана спектрограмма вокального пассажа с вибрато. По ней легко определить такие характеристики голоса, как частота и глубина вибрато, его форма и ровность, наличие певческой форманты. По изменению высоты основного тона и гармоник прослеживается исполняемая мелодия.

(наведите мышь для выбора изображения)

Современные средства реставрации звука, такие как программа iZotope RX, активно используют спектрограмму для редактирования отдельных частотно-временных областей в сигнале. С помощью этой техники можно найти и подавить такие нежелательные призвуки, как звонок мобильного телефона во время важной записи, скрип стула пианиста, кашель в зрительном зале и т.п.

Проиллюстрируем использование спектрограммы для удаления свиста поклонников из концертной записи.

На рис. 8 свист легко находится: это светлая кривая линия в районе 3 кГц. Если бы частота свиста была постоянной, то его можно было бы подавить с помощью режекторного фильтра. Однако в нашем случае частота меняется. Для выделения свиста на спектрограмме удобно воспользоваться инструментом «волшебная палочка» из программы iZotope RX II. Одно нажатие приводит к выделению основного тона свиста, повторное нажатие выделяет гармоники. После этого свист можно удалить, просто нажав на клавишу Del. Однако более аккуратный способ – воспользоваться модулем Spectral Repair: это позволит избежать «дыр» в спектре после удаления свиста. После применения этого модуля в режиме ослабления с вертикальной интерполяцией (Attenuate vertically) свист практически полностью исчезает из записи: как визуально, так и на слух.

Еще одно полезное применение спектрограммы – анализ присутствия в записи следов компрессии MP3 или других кодеков с потерями. У большинства записей оригинального (несжатого) качества частотный диапазон простирается до 20 кГц и выше; при этом энергия сигнала плавно спадает с ростом частоты (как на рис. 6, 7). В результате психоакустической компрессии верхние частоты сигнала квантуются сильнее нижних, и верхняя граница спектра сигнала обнуляется (как на рис. 8). При этом частота среза зависит от содержания кодируемого сигнала и от битрейта кодера. Ясно, что кодер стремится обнулять только те частоты в сигнале, которые в данный момент не слышны (замаскированы). Поэтому частота среза, как правило, меняется во времени, что образует на спектрограмме характерную «бахрому» с островками энергии на тёмном фоне.

Спектрограмма часто позволяет найти в записи дефекты, которые неочевидны при прослушивании, но могут сказаться при последующей обработке. Например, паразитная наводка от ЭЛТ-видеомонитора на частоте 15–16 кГц может ускользнуть от уха пожилого звукорежиссёра. Однако спектрограмма ясно покажет её в виде горизонтальной линии (рис. 9) и позволит уточнить частоту для настройки режекторного фильтра.

Аналогичная ситуация иногда возникает и с низкочастотными помехами, такими как задувание ветра в микрофон или постоянная составляющая (смещение по постоянному току, DC offset). Они могут располагаться на инфранизких частотах и не обнаруживать себя без помощи спектроанализатора или осциллографа.

Среди опытных звукорежиссёров старой школы распространено мнение, что анализировать и редактировать сигналы следует исключительно на слух, не полагаясь на индикаторы и анализаторы. Разумеется, анализаторы – не панацея в случае отсутствия слуха. Вряд ли кто-то серьёзно воспринимает идею сведения композиции «по приборам».

Не отрицая важности критического прослушивания звука на каждой стадии редактирования, мы всё же предлагаем использовать анализаторы спектра в тех задачах, где это может привести к более точным результатам. Конечно, можно определить на слух паразитный тон на частоте 15 кГц и подобрать режекторный фильтр подходящей добротности для его удаления. Но намного проще увидеть этот тон на спектроанализаторе и сразу более точно оценить его свойства: «плывёт» ли частота, есть ли боковые пики. В конечном счёте, это позволит более аккуратно удалить помеху. Аналогичная ситуация и со многими другими задачами редактирования, особенно – в реставрации звука.

Спектр и спектрограмма – способы представления звука, более близкие к слуховому восприятию, нежели осциллограмма. Надеюсь, что эта статья откроет новые возможности в анализе и редактировании звука для тех, кто ранее с этими представлениями не работал.

источник

Вкусненькое! (1730)
Напитки (37)
Шашлык (10)
Познавательно (255)
Красота и здоровье (233)
Полезные сайты и программы (216)
Психология (206)
Фотографии (205)
Книги (184)
Мудрость (167)
Музыка (160)
Cоветы (138)
Видео (126)
Жизнь (84)
География (82)
История (67)
Мужчины и женщины (64)
Астрология (62)
Города (57)
Обучение и языки (48)
Болезни (44)
Животные (43)
Стихи (42)
Юмор (36)
Заработать (32)
Архитектура (29)
Авики (29)
Картинки (26)
Справочник по ЛиРу (17)
МЕЧТА (9)

Цитата. Расшифровка анализа крови. Автоматический анализ с аббревиатурами на английском языке.

Второй месяц не проходит кашель. Несильный, сухой, не частый. Но все же не проходит и пошел к терапевту. Послушала — легкие чистые. Назначила таблетки, полоскания, ингаляции, флюорографию, общий анализ крови. Все вроде зашибись, но пришел сегодня к ней — а она не может расшифровать анализ крови. Мол прислали с автоматической лаборатории и она этих аббревиатур не знает. Вот нашел в инете, выложу сюда и завтра ей распечатку отнесу. Учиться никогда не поздно.
(Уже сегодня и УЗИ сердца делал, а завтра ФГС — что-то я боюсь, ни разу такую кишку не глотал. Бррр.

Расшифровка общего анализа крови осуществляется в несколько этапов, во время которых оцениваются основные показатели крови. Современные лаборатории оснащены оборудованием, проводящим автоматическое определение основных параметров крови. Такое оборудование обычно выдает результаты анализа в виде распечатки, в которой основные параметры крови обозначены аббревиатурами на английском языке. Ниже в таблице будут представлены основные показатели общего анализа крови, соответствующие им английские аббревиатуры и нормы.

Что это означает

Число эритроцитов (RBC — английская аббревиатура red blood cell count – количество красных кровяных телец).

Эритроциты выполняют важную функцию питания тканей организма кислородом, а также удаления из тканей углекислого газа, который затем выделяется через легкие. Если уровень эритроцитов ниже нормы (анемия) организм получает недостаточные количества кислорода. Если уровень эритроцитов выше нормы (полицитемия, или эритроцитоз) имеется высокий риск того, что красные кровные клетки склеятся между собой и заблокируют движение крови по сосудам (тромбоз).

4.3-6.2 х 10 в 12 степени /л для мужчин

3.8-5.5 х 10 в 12 степени /л для женщин

3.8-5.5 х 10 в 12 степени /л для детей

Гемоглобин (HGB, Hb)

Гемоглобин – это особый белок, который содержится в эритроцитах и отвечает за перенос кислорода к органам. Снижение уровня гемоглобина (анемия) приводит к кислородному голоданию организма. Повышение уровня гемоглобина, как правило, говорит о высоком количестве эритроцитов, либо об обезвоживании организма.

Гематокрит (HCT)

Гематокрит — это показатель, который отражает, какой объем крови занимают эритроциты. Гематокрит, как правило, выражается в процентах: например, гематокрит (НСТ) 39% означает, что 39% объема крови представлено красными кровяными тельцами. Повышенный гематокрит встречается при эритроцитозах (повышенное количество эритроцитов в крови), а также при обезвоживании организма. Снижение гематокрита указывает на анемию (снижение уровня эритроцитов в крови), либо на увеличение количества жидкой части крови.

Ширина распределения эритроцитов (RDWc)

Ширина распределения эритроцитов — это показатель, который говорит о том, насколько сильно эритроциты отличаются между собой по размерам. Если в крови присутствуют и крупные и мелкие эритроциты, ширина распределения будет выше, такое состояние называется анизоцитозом. Анизоцитоз — это признак железодефицитной и др. видов анемий.

Средний объем эритроцита (MCV)

Средний объем эритроцита позволяет врачу получить данные о размерах эритроцита. Средний объем эритроцита (MCV) выражается в фемтолитрах (фл), либо в кубических микрометрах (мкм3). Эритроциты с малым средним объемом встречаются при микроцитарной анемии, железодефицитной анемии и пр. Эритроциты с повышенным средним объемом встречаются при мегалобластной анемии (анемия, которая развивается при дефиците в организме витамина В12, либо фолиевой кислоты).

Среднее содержание гемоглобина в эритроците (MCH)

Показатель среднего содержания гемоглобина в эритроците позволяет врачу определить, сколько гемоглобина содержится в одном эритроците. Среднее содержание гемоглобина в эритроците, MCH, выражается в пикограммах (пг). Снижение этого показателя встречается при железодефицитной анемии, увеличение – при мегалобластной анемии (при дефиците витамина В12 или фолиевой кислоты).

Средняя концентрация гемоглобина в эритроците (МСНС)

Средняя концентрация гемоглобина в эритроците отражает, насколько эритроцит насыщен гемоглобином. Снижение этого показателя встречается при железодефицитных анемиях, а также при талассемии (врожденное заболевание крови). Повышение этого показателя практически не встречается.

Число тромбоцитов (кровяных пластинок, PLT -английская аббревиатура platelets — пластинки)

Тромбоциты – это небольшие пластинки крови, которые участвуют в образовании тромба и препятствуют потере крови при повреждениях сосудов. Повышение уровня тромбоцитов в крови встречается при некоторых заболеваниях крови, а также после операций, после удаления селезенки. Снижение уровня тромбоцитов встречается при некоторых врожденных заболеваниях крови, апластической анемии (нарушение работы костного мозга, который вырабатывает кровяные клетки), идиопатической тромбоцитопенической пурпуре (разрушение тромбоцитов из-за повышенной активности иммунной системы), циррозе печени и др.

Число лейкоцитов (WBC — английская аббревиатура white blood cell count — количество белых кровяных телец)

Лейкоциты (белые кровяные тельца) защищают организм от инфекций (бактерий, вирусов, паразитов). Лейкоциты по размерам превышают эритроциты, однако содержатся в крови в гораздо меньшем количестве. Высокий уровень лейкоцитов говорит о наличии бактериальной инфекции, а снижение числа лейкоцитов встречается при приеме некоторых лекарств, заболеваниях крови и др.

Содержание лимфоцитов (LYM английское сокращение, LY% процентное содержание лимфоцитов)

Лимфоцит – это вид лейкоцита, который отвечает за выработку иммунитета и борьбу с микробами и вирусами. Количество лимфоцитов в разных анализах может быть представлено в виде абсолютного числа (сколько лимфоцитов было обнаружено), либо в виде процентного соотношения (какой процент от общего числа лейкоцитов составляют лимфоциты). Абсолютное число лимфоцитов, как правило, обозначается LYM# или LYM. Процентное содержание лимфоцитов обозначают как LYM% или LY%. Увеличение числа лимфоцитов (лимфоцитоз) встречается при некоторых инфекционных заболеваниях (краснуха, грипп, токсоплазмоз, инфекционный мононуклеоз, вирусный гепатит и др.), а также при заболеваниях крови (хронический лимфолейкоз и др). Уменьшение числа лимфоцитов (лимфопения) встречается при тяжелых хронических заболеваниях, СПИДе, почечной недостаточности, приеме некоторых лекарств, подавляющих иммунитет (кортикостероиды и др.).
Подробнее: Снижение и повышение уровня лимфоцитов в крови

LYM# 1,2 — 3,0х109/л (или 1,2-63,0 х 103/мкл)

Содержание смеси моноцитов, эозинофилов, базофилов и незрелых клеток (MID, MXD)

Моноциты, эозинофилы, базофилы и их предшественники циркулируют в крови в небольших количествах, поэтому нередко эти клетки объединяют в одну группу, которая обозначается как MID или MXD. Эта группа может выражаться в процентах от общего числа лейкоцитов (MXD%), либо абсолютным числом (MXD#, MID#). Эти виды клеток крови также относятся к лейкоцитам и выполняют важные функции (борьбу с паразитами, бактериями, развитие аллергических реакций и др.) Абсолютное и процентное содержание этого показателя повышается, если увеличивается число одного из видов клеток, входящих в его состав. Для определения характера изменений, как правило, изучают процентное соотношение каждого вида клеток (моноцитов, эозинофилов, базофилов и их предшественников).

Количество гранулоцитов (GRA, GRAN)

Гранулоциты – это лейкоциты, которые содержат гранулы (зернистые лейкоциты). Гранулоциты представлены 3 типами клеток: нейтрофилы, эозинофилы и базофилы. Эти клетки участвуют в борьбе с инфекциями, в воспалительных и аллергических реакциях. Количество гранулоцитов в различных анализах может выражаться в абсолютных показателях (GRA#) и в процентах от общего числа лейкоцитов(GRA%).

Гранулоциты, как правило, повышены при наличии воспаления в организме. Снижение уровня гранулоцитов встречается при апластической анемии (потеря способности костного мозга вырабатывать клетки крови), после приема некоторых лекарств, а также при системной красной волчанке (заболевание соединительной ткани) и др.

GRA# 1,2-6,8 х 109/л (или 1,2-6,8 х 103/мкл)

Количество моноцитов (MON)

Моноциты – это лейкоциты, которые, попав в сосуды, вскоре выходят из них в окружающие ткани, где превращаются в макрофагов (макрофаги – это клетки, которые поглощают и переваривают бактерий и погибшие клетки организма). Количество моноцитов в различных анализах может выражаться в абсолютных показателях (MON#) и в процентах от общего числа лейкоцитов (MON%). Повышенное содержание моноцитов встречается при некоторых инфекционных заболеваниях (туберкулез, инфекционный мононуклеоз, сифилис и др.), ревматоидном артрите, заболеваниях крови. Снижение уровня моноцитов встречается после тяжелых операций, приема лекарств, подавляющих иммунитет (кортикостероиды и др.).

MON# 0.1-0.7 х 109/л (или 0,1-0,7 х 103/мкл)

Скорость оседания эритроцитов, СОЭ, ESR.

Скорость оседания эритроцитов – это показатель, который косвенно отражает содержание белков в плазме крови. Повышенная СОЭ указывает на возможное воспаление в организме из-за увеличенного содержания воспалительных белков в крови. Кроме того, повышение СОЭ встречается при анемиях, злокачественных опухолях и др. Уменьшение СОЭ встречается нечасто и говорит о повышенном содержании эритроцитов в крови (эритроцитоз), либо о других заболеваниях крови.

Следует отметить, что некоторые лаборатории указывают в результат анализов другие нормы, то связано с наличием нескольких методик подсчета показателей. В таких случаях, интерпретация результатов общего анализа крови осуществляется по заданным нормам.

источник

You are using an outdated browser. Upgrade your browser today or install Google Chrome Frame to better experience this site.

Даже если Вы делаете только первые шаги в торговле, Вы наверняка успели заметить, какой объём информации предстоит изучить и отработать на практике. Чтобы свести к минимуму типичные ошибки новичков и двигаться к прибыли верным курсом, нужно выбирать проверенные и эффективные методики анализа и торговли.

Определять точку входа в сделку и прогнозировать движение цены помогает анализ VSA и его торговые сигналы. Именно они лежат в основе осознанной торговли и понимания глубинных механизмов рынка. Но чтобы применять их на практике, нужно разобраться, что они собой представляют и как определять такие сигналы на графике. Об этом речь и пойдёт в нашей статье.

В переводе с английского расшифровка аббревиатуры VSA — Volume Spread Analysis, звучит как «анализ спреда и объёма». Отсюда можно сделать вывод о ключевых элементах такого анализа.

Благодаря детальному изучению спреда и объёма, трейдер может заметить, как ведут себя крупные игроки рынка – маркет-мейкеры, и, проследив за их поведением, с высокой точностью спрогнозировать ценовое движение. Методика была разработана Ричардом Вайкоффом и дополнена Томом Вильямсом, придавшим ей современный облик.

На практике, анализ VSA применяется к графикам цены актива. Допустим, изучая график, трейдер видит, что цена медленно идёт вверх на стабильно высоком объёме, а потом резко пробивает уровень сопротивления. Обычный трейдер, не знакомый с методикой VSA поспешит открыть позицию, предвидя новый тренд, тогда как опытный трейдер обратит внимание на объёмы после этого резкого пробития. Если они остаются высокими, то, вероятнее всего, цену ожидает отскок от уровня и разворот, а не восходящий тренд. Трейдер, знакомый с анализом объёмов понимает, что в такой ситуации крупные игроки, скорее всего, долгое время набирали позиции для продажи, а скачок цены был нужен лишь затем, чтобы заманить неопытных трейдеров и потом вынести их по стопам резким ценовым разворотом.

Как видно, анализ VSA помогает правильно интерпретировать движения цены, видеть, кто за ними стоит, и избегать убытков из-за манипуляций биржевых монстров.

Цена на рынке никогда не движется беспричинно. Любое усилие порождает результат, а если его нет, значит, в игру вмешиваются третьи силы – маркет-мейкеры. По таким параметрам, как сила и слабость рынка, зоны перекупленности и перепроданности можно умело определять реальную рыночную ситуацию и прогнозировать изменения, а также замечать манипуляции профессиональных участников рынка.

Замечать и использовать эти параметры в своей торговле помогает именно анализ VSA. Этот метод интересен и универсален, его можно применять на любых рынках, с большинством торговых инструментов в позиционной торговле.

Ключевые элементы такого анализа – спред, объём и цена. Анализируя график системно, бар за баром, трейдер обретает полую картинку рыночной ситуации. Для удобства систематизации такого анализа, были выделены сигналы VSA – своеобразные алгоритмы поведения цены, её закономерности, объясняющие поведение крупных игроков. Всего насчитывается более 200 таких сигналов, но ниже мы рассмотрим наиболее часто встречающиеся на графиках.

Английское название сигнала	Расшифровка сигнала на английском	Русская расшифровка сигнала VSA	Пояснение
SA	Stopping Action	Останавливающее действие	Указывает на остановку движения цены. При достаточной силе покупателя является сигналом к покупке, при слабости рынка указывает на скорый разворот восходящего тренда.
SOT	Shorting of Thrust	Продажа попытки	Когда цена идет вверх, пытается преодолеть какой-то уровень, но эту попытку кто-то продает. Сигнал является противоположным сигналу SA и указывает на манипуляции крупных игроков.
Spring	Spring	Спринг

(спружинивание)

Обновление минимума цены, после которого она «пружинит» и быстро идет в обратную сторону.
Сигнал манипуляции. Up-Thrust Up-Thrust up- вверх,

thrust — попытка

Попытка выйти вверх, т.е. не разворот, а попытка цены преодолеть какое-то сопротивление.
Сигнал манипуляции. JOC Jump over Creek Прыжок через ручей Характеризуется резким движением цены с выходом из торгового ренджа. Важно оценить силу прыжка и увидеть его результат: удачно прыгнули или нет. BTC Back to Creek Возврат к ручью Возвращение цены к уровню сопротивления, ставшему уровнем поддержки. Определяется результатом скачка цены и ее скоростью возврата на прежний уровень для тестирования. BUI Break under Ice Провалиться под лед Резкий провал цены ниже условного уровня Ice.Предусматривает два варианта развития событий: цена либо выпрыгнет обратно, либо нет. BTI Back to Ice Возврат к уровню ice Движение цены снизу вверх, возврат к уровню Ice.

Важный момент в правильной интерпретации этих сигналов – учёт контекста рынка. Сигналы нельзя воспринимать как готовые паттерны, дающие однозначный ответ на вопрос о направлении цены. В каждом отдельном случае важно учитывать левую часть графика и рыночные объёмы, только тогда сигналы VSA станут полезным и эффективным инструментом трейдера. Всегда необходимо думать и анализировать самостоятельно: хороший был пробой уровня или нет, какими объемами он формировался? Следует также обращать внимание на то, какой результат и прогресс, в виде силы и направления движения цены мы получили.

Умение эффективно определять, куда пойдёт цена на графике – ключевой навык трейдера для прибыльной торговли. То, насколько точно трейдер сможет делать такие прогнозы, во многом зависит от используемого им метода анализа. Сегодня мы узнали, что анализ VSA – удобный, эффективный и универсальный инструмент, который даёт трейдеру большое преимущество, позволяя видеть за ценовым движением действия рыночных монстров и не ловиться на их манипуляции.

Изучение метода и сигналов VSA – кропотливый, но интересный и результативный труд. В нашем блоге немалое количество статей посвящено именно этому методу анализа. Чтобы быть в курсе последних трендов по анализу объёмов и других нюансов торговли, оформите подписку на наш блог, и получайте свежие статьи первыми. Если у Вас остались какие-либо вопросы, -пишите комментарии, мы на них обьязательно ответим!

источник

Вейвлет – преобразование сигналов является обобщением спектрального анализа, типичный представитель которого – классическое преобразование Фурье. Термин «вейвлет» (англ. wavelet ) в переводе с английского означает «маленькая (короткая) волна». Вейвлеты — это обобщенное название семейств математических функций определенной формы, которые локальны во времени и по частоте, и в которых все функции получаются из одной базовой (порождающей) посредством ее сдвигов и растяжений по оси времени. Вейвлет-преобразования рассматривают анализируемые временные функции в терминах колебаний, локализованных по времени и частоте. Как правило, вейвлет-преобразования (WT) подразделяют на дискретное (DWT) и непрерывное (CWT).

DWT используется для преобразований и кодирования сигналов, CWT — для анализа сигналов. Вейвлет-преобразования в настоящее время принимаются на вооружение для огромного числа разнообразных применений, нередко заменяя обычное преобразование Фурье. Это наблюдается во многих областях, включая молекулярную динамику, квантовую механику, астрофизику, геофизику, оптику, компьютерную графику и обработку изображений, анализ ДНК, исследования бел-ков, исследования климата, общую обработку сигналов и распознавание речи.

Вейвлетный анализ представляет собой особый тип линейного преобразования сигналов и отображаемых этими сигналами физических данных о процессах и физических свойствах природных сред и объектов. Базис собственных функций, по которому проводится вейвлетное разложение сигналов, обладает многими специфическими свойствами и возможностями. Вейвлетные функции базиса позволяют сконцентрировать внимание на тех или иных локальных особенностях анализируемых процессов, которые не могут быть выявлены с помощью традиционных преобразований Фурье и Лапласа. К таким процессам в геофизике относятся поля различных физических параметров природных сред. В первую очередь это касается полей температуры, давления, профилей сейсмических трасс и других физических величин. Принципиальное значение имеет возможность вейвлетов анализировать нестационарные сигналы с изменением компонентного содержания во времени или в пространстве.

Вейвлеты имеют вид коротких волновых пакетов с нулевым интегральным значением, локализованных по оси аргументов (независимых переменных), инвариантных к сдвигу и линейных к операции масштабирования (сжатия/растяжения). По локализации во временном и частотном представлении вейвлеты занимают промежуточное положение между гармоническими (синусоидальными) функциями, локализованными по частоте, и функцией Дирака, локализованной во времени.

Теория вейвлетов не является фундаментальной теорией, но она дает удобный и эффективный инструмент для решения многих практических задач. Основная область применения вейвлетных преобразований – анализ и обработка сигналов и функций, нестационарных во времени или неоднородных в пространстве, когда результаты анализа должны содержать не только общую частотную характеристику сигнала (распределение энергии сигнала по частотным составляющим), но и сведения об определенных локальных координатах, на которых проявляют себя те или иные группы частотных составляющих, или на которых происходят быстрые изменения частотных составляющих сигнала. По сравнению с разложением сигналов на ряды Фурье, вейвлеты способны с гораздо более высокой точностью представлять локальные особенности сигналов, вплоть до разрывов 1-го рода (скачков). В отличие от преобразований Фурье, вейвлет-преобразование одномерных сигналов обеспечивает двумерную развертку, при этом частота и координата рассматриваются как независимые переменные, что дает возможность анализа сигналов сразу в двух пространствах.

Одна из главных и особенно плодотворных идей вейвлетного представления сигналов на различных уровнях декомпозиции (разложения) заключается в разделении функций приближения к сигналу на две группы: аппроксимирующую — грубую, с достаточно медленной временной динамикой изменений, и детализирующую — с локальной и быстрой динамикой изменений на фоне плавной динамики, с последующим их дроблением и детализацией на других уровнях декомпозиции сигналов. Это возможно как во временной, так и в частотной областях представления сигналов вейвлетами.

История спектрального анализа восходит к И. Бернулли, Эйлеру и Фурье, который впервые построил теорию разложения функций в тригонометрические ряды. Однако это разложение долгое время применялось как математический прием и не связывалось с какими-либо физическими понятиями. Спектральные представления применялись и развивались лишь сравнительно узким кругом физиков–теоретиков. Однако, начиная с 20-х годов прошлого века, в связи с бурным развитием радиотехники и акустики, спектральные разложения приобрели физический смысл и практическое применение. Основным средством анализа реальных физических процессов стал гармонический анализ, а математической основой анализа — преобразование Фурье. Преобразование Фурье разлагает произвольный процесс на элементарные гармонические колебания с различными частотами, а все необходимые свойства и формулы выражаются с помощью одной базисной функции e j ω t \,\!> или двух действительных функций sin ⁡ ( ω t ) и cos ⁡ ( ω t ) . Гармонические колебания имеют широкое распространение в природе, и поэтому смысл преобразования Фурье интуитивно понятен независимо от математической аналитики.

Было также установлено, что функции можно разложить не только по синусам и косинусам, но и по другим ортогональным базисным системам, например, полиномам Лежандра и Чебышева, функциям Лагерра и Эрмита. Однако практическое применение они получили только в последние десятилетия ХХ века благодаря развитию вычислительной техники и методов синтеза цифровых линейных систем обработки данных. Тем не менее, непосредственно для целей спектрального анализа подобные ортогональные функции не нашли широкого применения из-за трудностей интерпретации получаемых результатов. По тем же причинам не получили развития в спектральном анализе функции типа «прямоугольной волны» Хаара, Радемахера, Уолша, Крестенсена.

Теоретические исследования ортогональных базисных систем общего вида привели к созданию теории обобщенного спектрального анализа, которая позволила оценить пределы практического применения классического спектрального анализа Фурье, и создала методы и критерии синтеза базисных систем для решения конкретных практических задач. Иллюстрацией этому является активно развивающаяся с начала 80-х годов прошлого столетия теория базисных функций типа вейвлет. Благодаря прозрачности физической интерпретации результатов анализа, сходной с «частотным» подходом в преобразовании Фурье, ортогональный базис вейвлетов стал популярным и эффективным средством анализа нестационарных сигналов и изображений в акустике, сейсмике, медицине и других областях.

Вейвлет-анализ является разновидностью спектрального анализа, в котором роль простых колебаний играют функции особого рода, называемые вейвлетами. Базисная функция вейвлет – это некоторое «короткое» колебание, но не только. Понятие частоты классического спектрального анализа здесь заменено масштабом, и, чтобы перекрыть «короткими волнами» всю временную ось, введен сдвиг функций во времени. Таким

Сам термин «вейвлет», как понятие, ввели в своей статье J. Morlet и A. Grossman, опубликованной в 1984 г. Они занимались исследованиями сейсмических сигналов с помощью базиса, который назвали вейвлетом. Эта работа дала начало развитию вейвлетов в течение последующих десяти лет целому ряду авторов. Весомый вклад в теорию вейвлетов внесли Гуппилауд, Гроссман и Морлет, сформулировавшие основы CWT, Жан Олаф-Стромберг с ранними работами по дискретным вэйвлетам, Ингрид Добеши, разработавшая ортогональные вейвлеты (1988), Натали Делпрат, создавшая время-частотную интерпретацию CWT (1991), Ньюланд, разработавший гармоническое вейвлет-преобразование, и многие другие. Математическая формализация, данная работами Mallat и Meyer, привела к созданию теоретических основ вейвлет-анализа, названного мультиразрешающим (кратномасштабным) анализом.

В настоящее время специальные пакеты расширений по вейвлетам уже присутствуют в основных системах компьютерной математики (Matlab, Mathematica, Mathcad, и др.), а вейвлет-преобразования и вейвлетный анализ используются во многих областях науки и техники для са-мых различных задач: для распознавания образов, численного моделирования динамики сложных нелинейных процессов, анализа аппаратной информации и изображений в медицине, космической технике, астрономии, геофизике, для эффективного сжатия сигналов и передачи информации по каналам с ограниченной пропускной способностью и т.п. Многие исследователи называют вейвлет-анализ «математическим микроскопом» для точного изучения внутреннего состава и структур неоднородных сигналов и функций.

Не следует рассматривать вейвлет-методы обработки и анализа сигналов в качестве новой универсальной технологии для решения любых задач. Возможности вейвлетов, несомненно, еще не раскрыты полностью. Однако это не означает, что их развитие приведет к полной замене традиционных средств обработки и анализа информации, хорошо отработанных и проверенных временем. Но оно может существенно расширить инструментальную базу информационных технологий обработки данных.

всегда может быть создана система ортонормированных «осей» (базис пространства), при этом любой сигнал, принадлежащий этому пространству, может быть представлен в виде весовой суммы проекций сигнала на эти «оси» – базисных векторов. Значения проекций определяются скалярными произведениями сигнала с соответствующими функциями базисных «осей». Базис пространства может быть образован любой ортогональной системой функций. Наибольшее применение в спектральном анализе получила система комплексных экспоненциальных функций. Проекции сигнала на данный базис определяются выражением:

Для коэффициентов ряда Фурье справедливо равенство Парсеваля сохранения энергии сигнала в различных представлениях:

при этом она может быть периодически расширена и определена на всей временной оси пространства R ( − ∞ , ∞ ) так, что

при условии сохранения конечности энергии в пространстве R ( − ∞ , ∞ ) .

С позиций анализа произвольных сигналов и функций в частотной области и точного восстановления после преобразований можно отметить ряд недостатков разложения сигналов в ряды Фурье, которые привели к появлению оконного преобразования Фурье и стимулировали развитие вейвлетного преобразования. Основные из них:

Ограниченная информативность анализа нестационарных сигналов и практически полное отсутствие возможностей анализа их особенностей (сингулярностей), т.к. в частотной области происходит «размазывание» особенностей сигналов (разрывов, ступенек, пиков и т.п.) по всему частотному диапазону спектра.
Гармонические базисные функции разложения не способны в принципе отображать перепады сигналов с бесконечной крутизной типа прямоугольных импульсов, т.к. для этого требуется бесконечно большое число членов ряда. При ограничении числа членов ряда Фурье в окрестностях скачков и разрывов восстановленного сигнала возникают осцилляции (явление Гиббса).
Преобразование Фурье отображает глобальные сведения о частотах исследуемого сигнала и не дает представления о локальных свойствах сигнала при быстрых временных изменения его спектрального состава. Так, например, преобразование Фурье не различает сигнал с суммой двух синусоид (стационарный сигнал), от сигнала с двумя последовательно следующими синусоидами с теми же частотами (нестационарный сигнал), т.к. спектральные коэффициенты ( 1.2 ) (1.2)\,\!> вычисляются интегрированием по всему интервалу задания сигнала. Преобразование Фурье в принципе не имеет возможности анализировать частотные характеристики сигнала в произвольные моменты времени.

Частичным выходом из этой ситуации является оконное преобразование Фурье с движущейся по сигналу оконной функцией, имеющей компактный носитель. Временной интервал сигнала при большой его длительности разделяется на подинтервалы, и преобразование Фурье выполняется последовательно для каждого подинтервала в отдельности. Тем самым осуществляется переход к частотно-временному (частотно-координатному) представлению сигналов, при этом в пределах каждого подинтервала сигнал «считается» стационарным. Результатом оконного преобразования является семейство спектров, которым отображается изменение спектра сигнала по интервалам сдвига окна преобразования. Это в какой-то мере позволяет выделять на координатной оси и анализировать особенности нестационарных сигналов. Размер носителя оконной функции w ( t ) обычно устанавливается соизмеримым с интервалом стационарности сигнала. По существу, таким преобразованием один нелокализованный базис разбивается на определенное количество базисов, локализованных в пределах функции w ( t ) , что позволяет представлять результат преобразования в виде функции двух переменных — частоты и временного положения окна. При этом размер стационарности сигнала необходимо знать априори.

Оконное преобразование выполняется в соответствии с выражением:

Пример оконного преобразования для нестационарного сигнала на большом уровне шума приведен на рис. 1.2. По спектру сигнала в целом можно судить о наличии в его составе гармонических колебаний на трех частотах. Оконное преобразование не только подтверждает данное заключение, но и показывает конкретную локальность колебаний по интервалу сигнала и соотношение между амплитудами этих колебаний.

Частотно-временное оконное преобразование применяется для анализа нестационарных сигналов, если их частотный состав изменяется во времени. Функция оконного преобразования ( 1.7 ) (1.7)\,\!> может быть переведена в трехмерный вариант с независимыми переменными и по времени, и по частоте:

Как видно по результатам вычислений, оконное преобразование позволяет информативные особенности сигнала и по времени, и по частоте. Разрешающая способность локализации определяется принципом неопределенности Гейзенберга, который гласит, что невозможно получить произвольно точное частотно-временное представление сигнала, то есть нельзя определить для какого-то момента времени, какие спектральные компоненты присутствуют в сигнале. Чем уже окно, тем лучше временное разрешение, но хуже частотное, и наоборот. Кроме того, чем уже окно, тем более справедливыми становятся наши предположения о стационарности сигнала в пределах окна.

На рис. 1.4 приведен пример частотно-временного оконного преобразования сигнала, состоящего из 4-х непересекающихся интервалов, в каждом из которых сумма двух гармоник разной частоты, гауссовой оконной функцией разной ширины. Узкое окно обеспечивает лучшее временное разрешение и четкую фиксацию границ интервалов, но широкие пики частот в пределах интервалов. Широкое окно напротив – четко отмечает частоты интервалов, но с перекрытием границ временных интервалов. При решении практических задач приходится выбирать окно для анализа всего сигнала, тогда как разные его участки могут требовать применения разных окон. Если сигнал состоит из далеко отстоящих друг от друга частотных компонент, то можно пожертвовать спектральным разрешением в пользу временного, и наоборот.

Функции оконного спектрального анализа в Mathcad находятся в пакете Signal Processing. Они позволяют разбивать сигнал на поддиапазоны (с перекрытием или без перекрытия) и выполнять следующие операции:

cspectrum(x,n,r[,w]) – расчет кросс-спектра сигнала х;
pspectrum(x,n,r[,w]) – расчет распределения спектральной мощности сигнала;
coherence(x,y,n,r[,w]) – расчет когерентности сигналов х и у;
snr(x,y,n,r[,w]) – расчет отношения сигнал/шум для векторов х и у.

Здесь: х и у – вещественные или комплексные массивы данных (векторы), n – число поддиапазонов разбиения входного сигнала х (от 1 до N – размера массива), к – фактор перекрытия поддиапазонов (от 0 до 1), w — код окна (1- прямоугольное, 2- трапеция, 3- треугольное, 4- окно Хеннинга, 5- окно Хемминга, 6- окно Блекмана).

Отличительной особенностью вейвлет-анализа является то, что в нем можно использовать семейства функций, реализующих различные варианты соотношения неопределенности. Соответственно, исследователь имеет возможность гибкого выбора между ними и применения тех вейвлетных функций, которые наиболее эффективно решают поставленные задачи.

где коэффициенты представления сигнала – проекции сигнала на новый ортогональный базис функций, как и в преобразовании Фурье, определяются скалярным произведением

источник